Свойства окружности, описанной вокруг трапеции
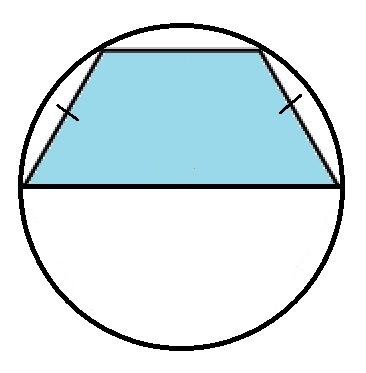
Окружность, описанная около трапеции
Трапеция — это выпуклый четырехугольник, две стороны которого параллельны, а две другие — не параллельны.
Около четырехугольника можно описать окружность, если сумма его противолежащих углов равна 180°. Поэтому окружность можно описать только вокруг равнобедренной трапеции.
Как найти радиус описанной окружности
Самый распространенный способ найти радиус окружности, описанной около трапеции — через радиус окружности, описанной около треугольника, имеющего 3 любые общие вершины с данной трапецией.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Каждая диагональ делит трапецию на два треугольника. Описанная окружность проходит через все вершины трапеции, значит она проходит через все вершины каждого из этих треугольников и также является для них описанной окружностью.
Если известны угол и диагональ трапеции
\(R=\frac а{2\cdot\sin\alpha},\)
где R — радиус описанной окружности,
а — сторона треугольника,
α — угол треугольника, противолежащий стороне а.
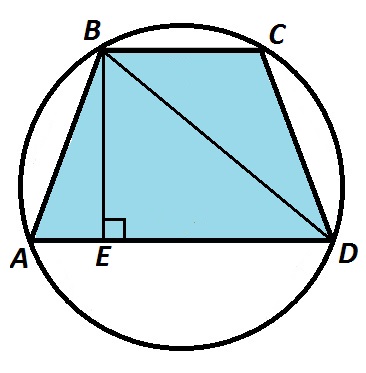
Например, если известна диагональ BD=а и острый угол трапеции ABCD ∠CDA=β, то можем найти радиус описанной окружности.
Рассмотрим треугольник BCD. Сторона BD известна. \(∠BCD=180°-∠CDA=180°-β\).
Радиус описанной окружности будет равен \(\frac а{2\cdot\sin\left(180^\circ-\beta\right)}\).
Если известны диагональ, стороны трапеции и площадь одного из треугольников
\(R=\frac{abc}{4S}\),
где R — радиус описанной окружности,
а, b, c — стороны треугольника,
S — площадь треугольника.
Если известны длины сторон треугольника
\(R=\frac{abc}{4\sqrt{p\left(p-a\right)\left(p-b\right)\left(p-c\right)}},\)
где R — радиус описанной окружности,
а, b, c — стороны треугольника,
p — ½ периметра треугольника.
Как найти центр описанной окружности
Центр описанной окружности может лежать как внутри трапеции, так и вне ее. Определить его местонахождение помогает угол между диагональю трапеции и боковой стороной.
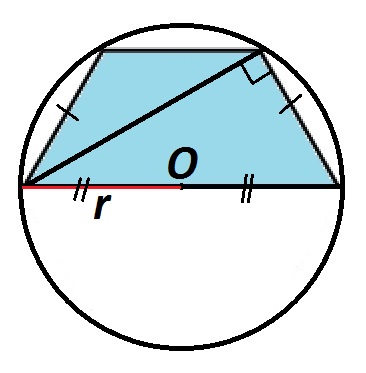
Если угол прямой
Если диагональ трапеции перпендикулярна ее боковой стороне, то центр описанной окружности будет лежать на середине большего основания. Тогда большее основание будет равно диаметру описанной окружности.
\(R=\frac12а,\)
где R — радиус описанной окружности,
а — большее основание трапеции.
Если угол острый
Если диагональ трапеции и боковая сторона образуют острый угол, то центр описанной около трапеции окружности лежит внутри трапеции.
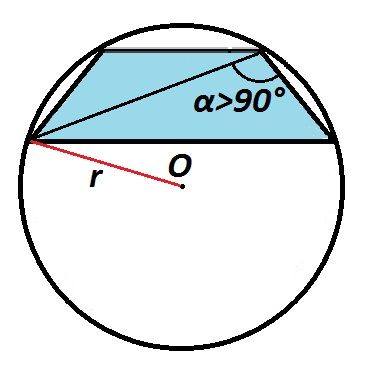
Если угол тупой
Если диагональ трапеции и боковая сторона образуют тупой угол, то центр описанной около трапеции окружности будет лежать вне трапеции за ее большим основанием.
Задачи с решениями
Дано: трапеция с описанной окружностью. Периметр трапеции равен 22 см, а ее средняя линия — 5 см.
Найти: боковую сторону трапеции.
Решение: Так как около трапеции описана окружность, эта трапеция — равнобедренная. Удвоенная средняя линия трапеции равна сумме ее оснований (10 см). Сумма двух боковых сторон равна 22-10=12 (см). Боковая сторона трапеции равна 6 см.
Ответ: 6 см.
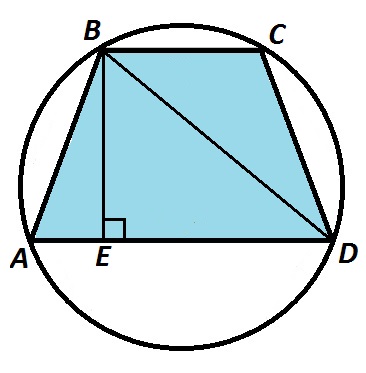
Дано: основания трапеции ВС=11 см и AD=21 см. Диагональ трапеции ВD=20 см.
Найти: радиус описанной окружности.
Решение: найдем радиус окружности, описанной около \(ΔABD. R=\frac{BD}{2\sin\angle A}.\)
- Трапеция ABCD равнобедренная, AB=CD, так как описать окружность можно только около равнобедренной трапеции.
- ВЕ — высота трапеции. Отрезок \(АЕ=(21-11):2=5 (см)\) по свойству равнобедренной трапеции. Отрезок ЕD=21-5=16 (см).
- Треугольник BED прямоугольный. ∠BED=90°. По теореме Пифагора \(BE=\sqrt{20^2-16^2}=12 (см).\)
- Треугольник АBE также прямоугольный. ∠BED=90°. По теореме Пифагора \(АВ=\sqrt{5^2+12^2}=13 (см).\)
- \(sin∠BAD=\frac{12}{13}\) по определению синуса.
- \(R=\frac{BD}{2\sin\angle A}=10\frac56 (см).\)
Ответ: \(10\frac56 см.\)
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так