Вычисление радиуса окружности, описанной около треугольника
Радиус описанной около треугольника окружности
Треугольник является геометрической фигурой на плоскости, которая включает три стороны в виде отрезков, образованных с помощью соединения трех точек, не лежащих на одной прямой.
Обозначают данную геометрическую фигуру символом △.
Точками A, B и C обычно обозначают вершины треугольника. Отрезки AB, BC и AC определяют стороны треугольника, которые, как правило, обозначают с помощью латинской буквы. К примеру, AB = a, BC = b, AC = c.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Внутренность треугольника представляет собой часть плоскости, которая ограничена сторонами треугольника. Стороны треугольника в вершинах формируют три угла, которые обычно обозначают, используя греческие буквы – \(\alpha, \beta, \gamma\) и другие. По этой причине треугольник получил название многоугольника с тремя углами. Для обозначения углов также применяют символ ∠, к примеру:
- \(\alpha \)∠BAC или ∠CAB;
- \(\beta\) ∠ABC или ∠CBA;
- \(\gamma \)∠ACB или ∠BCA.
Треугольники различают по величине углов или количеству равных сторон:
- остроугольный, в котором все три угла острые, то есть меньше \(90^{0}\);
- тупоугольный, обладает один из углов больше \(90^{0}\), а два остальных угла являются острыми;
- прямоугольный с одним прямым углом в \(90^{0}\), двумя сторонами, образующими прямой угол, которые называют катетами, третьей стороной, расположенной напротив прямого угла в виде гипотенузы;
- разносторонний, со сторонами разной длины;
- равнобедренный, с двумя одинаковыми боковыми сторонами и третьей стороной в виде основания, углы при котором равны;
- равносторонний (правильный) обладает тремя сторонами с одинаковой длиной и углами, равными по \(60^{0}\).
Окружностью называют замкнутую плоскую прямую, каждая точка которой равноудалена от данной точки или центра, лежащей в той же плоскости, что и кривая.
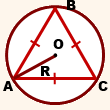
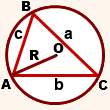
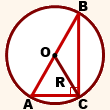
Окружность, описанная около треугольника, является окружностью, проходящей через все три вершины рассматриваемого треугольника.
Радиус окружности, описанной около треугольника, определяется с помощью специальных формул, подкрепленных соответствующими доказательствами. Первая закономерность позволяет рассчитать его согласно расширенной теореме синусов:
- радиус R окружности, описанной около треугольника, равен отношению стороны треугольника к удвоенному синусу противолежащего угла.
Формула для нахождения радиуса:
\(R=\frac{AB}{2\sin \angle C} =\frac{AC}{2\sin \angle B} =\frac{BC}{2\sin \angle A}\)
Вторую формулу для определения радиуса описанной около треугольника окружности записывают таким образом:
\(R=\frac{AB*BC*AC}{4S_{ABC}}\)
Общий вид:
\(R=\frac{abc}{4S}\)
Таким образом, для определения радиуса окружности, которая описана около треугольника, требуется произведение длины сторон этой геометрической фигуры разделить на четыре площади треугольника.
Площадь треугольника можно рассчитать, используя формулу Герона:
\(S=\sqrt{p(p-a)(p-b)(p-c)}\)
В данном случае р обозначает полупериметр и определяется по формуле:
\(p=\frac{a+b+c}{2}\)
В результате преобразованная формула для определения радиуса описанной около треугольника окружности примет следующий вид:
\(R=\frac{abc}{4\sqrt{p(p-a)(p-b)(p-c)}}\)
Представленные закономерности справедливы в случае любого треугольника, независимо от его вида. При расчетах необходимо учитывать расположение центра описанной окружности.
Расположение центра окружности, описанной около треугольника:
- остроугольный треугольник – во внутренней области;
- прямоугольный треугольник – на середине гипотенузы;
- тупоугольный треугольник – вне геометрической фигуры, напротив тупого угла.
Вычисление радиуса через стороны
Выше были рассмотрены формулы, с помощью которых можно определить радиус окружности, описанной вокруг треугольника, зная его стороны. Кроме того, при решении задач можно использовать некоторые закономерности, предусмотренные для треугольников определенного типа.
Формула для равнобедренного треугольника
Обладая информацией о длине сторон равнобедренного треугольника, можно определить радиус окружности, описанной вокруг этого треугольника.
\(R=\frac{a^{2}}{\sqrt{4a^{2}-b^{2}}}\)
где a и b являются сторонами треугольника.
Формула для равностороннего треугольника
Такое выражение подходит для расчета радиуса окружности, описанной около любого правильного многоугольника. Формула имеет вид:
\(R=\frac{a}{2\sin \frac{180^{0}}{n}}\)
Здесь а является длиной стороны многоугольника, n – определяет количество его сторон.
Частным случаем правильного многоугольника является правильный треугольник. Тогда данную формулу можно применить для расчета радиуса окружности, описанной около правильного треугольника.
Формула радиуса описанной окружности для правильного треугольника:
\(R=\frac{a}{\sqrt{3}}\)
Исключая иррациональность в знаменателе, получим:
\(R=\frac{a\sqrt{3}}{3}\)
Следует заметить, что в случае правильного треугольника радиус описанной окружности в два раза превышает радиус вписанной окружности:
R=2r
Формула для произвольного треугольника
Как правило, при решении задач по геометрии необходимо вычислить радиус окружности, описанной около произвольного треугольника. В этом случае целесообразно воспользоваться формулой:
\(R=\frac{abc}{4S}\)
Справедливо следующее равенство:
\(R=\frac{a}{2\sin \alpha }=\frac{b}{2\sin \beta }= \frac{c}{2\sin \gamma }\)
где a, b, c являются длинами сторон треугольника, \(\alpha, \beta, \gamma\) определяются, как противолежащие этим сторонам углы, S представляет собой площадь треугольника.
Формула для прямоугольного треугольника
Радиус описанной около прямоугольного треугольника окружности можно определить по формуле:
\(R=\frac{AB}{2}\)
Таким образом, в случае прямоугольного треугольника радиус окружности, которая описана около него, равен половине гипотенузы. Как правило, ее обозначают с помощью «с», то есть АВ = с. Поэтому формула принимает следующий вид:
\(R=\frac{c}{2}\)
Примеры решения задач
Задача 1
Стороны треугольника равны 4, 6 и 9 см. Необходимо определить радиус окружности, которая описана около данного треугольника.
Решение
В первую очередь нужно рассчитать площадь рассматриваемого треугольника. Зная длины его сторон, ее можно определить с помощью формулы Герона:
\(S=\sqrt{9.5(9.5-4)*(9.5-6)*(9.5-9)}\approx 9.56\)
Затем достаточно просто найти радиус окружности:
\(R=\frac{4*6*9}{4*9.56}\approx 5.65\)
Ответ: радиус окружности равен 5.65 см
Задача 2
Известно, что катеты прямоугольного треугольника равны 6 и 8 см. Требуется рассчитать радиус окружности, которая описана около данного треугольника.
Решение
Определим гипотенузу рассматриваемого треугольника с помощью теоремы Пифагора:
\(c=\sqrt{6^{2}+8^{2}}=10\)
Известно, что радиус окружности, которая описана около прямоугольного треугольника, соответствует половине его гипотенузы. Таким образом:
\(R = 10/2 = 5\)
Ответ: радиус окружности равен 5 см.
Задача 3
Необходимо определить радиус описанной окружности около треугольника АВС, стороны которого равны \(AB=4\sqrt{2}\) см,\(\ AC=7 см\) и \(\angle A=45^{\circ}.\)
Решение
Определить радиус окружности, которая описана около треугольника, можно, как отношение произведения сторон треугольника к его площади, умноженной на 4:
\(R=\frac{AB\cdot BC\cdot AC}{4S} \)
По теореме косинусов следует рассчитать сторону ВС:
\(BC=\sqrt{AC^2 +AB^2 -2AC\cdot AB\cdot \cos \angle A} =\)
\(=\sqrt{49+32-2\cdot 7\cdot 4\sqrt{2} \cdot \frac{\sqrt{2} }2 } =\sqrt{25} =5\ cm\)
Затем можно определить площадь треугольника АВС:
\(S_{ABC} =\frac{1}{2} \cdot AB\cdot AC\cdot \sin \angle A=14\ cm^2 \)
Зная площадь, легко рассчитать радиус окружности:
\(R=\frac{AB\cdot BC\cdot AC}{4S} =\frac{4\sqrt{2} \cdot 5\cdot 7}{4\cdot 14} =\frac{5\sqrt{2} }{2} \ cm\)
Ответ: радиус окружности равен \(\frac{5\sqrt{2} }2 см.\)
Задача 4
Дан треугольник АВС со сторонами AB=3 см,\(\ AC=\sqrt{6} см\). Необходимо определить углы этой геометрической фигуры. При этом радиус описанной окружности равен \(R=\sqrt{3}\) см.
Решение
Согласно формуле, радиус описанной окружности равен отношению стороны треугольника к удвоенному синусу противолежащего угла:
\(R=\frac{AB}{2\sin \angle C} =\frac{AC}{2\sin \angle B} =\frac{BC}{2\sin \angle A} \)
Таким образом, можно вычислить синусы углов треугольника:
\(\sin \angle C=\frac{AB}{2R} =\frac{3}{2\sqrt{3} } =\frac{\sqrt{3} }{2}, откуда \angle C=60^{\circ},\)
\(\sin \angle B=\frac{AC}{2R} =\frac{\sqrt{6} }{2\sqrt{3} } =\frac{\sqrt{2} }{2}, откуда \angle B=45^{\circ}.\)
Далее следует определить угол А:
\(\angle A=180^{\circ} -60^{\circ} -45^{\circ} =75^{\circ} \)
Ответ: \(\angle A=75^{\circ} ,\ \angle B=45^{\circ} ,\ \angle C=60^{\circ}\)
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так