Радиус вписанной в ромб окружности
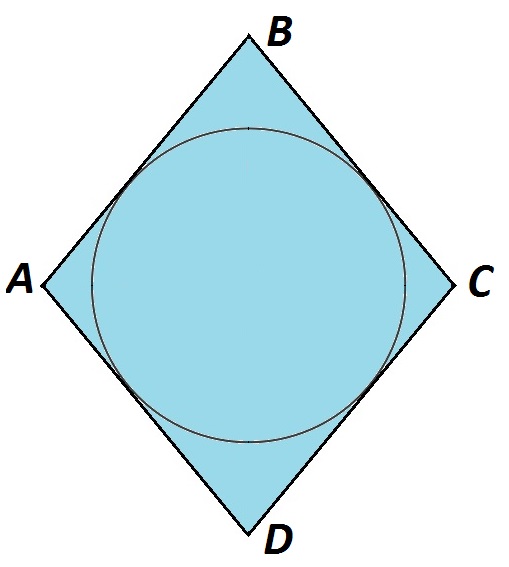
Окружность, вписанная в ромб
Ромб — это параллелограмм с четырьмя равными сторонами.
Квадрат — частный случай ромба; это ромб, все углы которого прямые.
Вписанная в ромб окружность — это окружность, которая лежит внутри ромба и касается всех его сторон.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Окружность можно вписать в многоугольник, у которого равны суммы противолежащих сторон. Ромб соответствует этому условию, поэтому в ромб можно вписать окружность.
Свойства ромба и вписанной окружности
- в любой ромб можно вписать окружность;
- точка пересечения диагоналей ромба является центром окружности, вписанной в ромб.
Как найти радиус, основные способы
Радиус вписанной окружности, если известны диагонали и сторона
Радиус r вписанной в ромб окружности равен произведению его диагоналей, деленному на периметр или на сторону, умноженную на 4.
\(r=\frac{d_1d_2}Р=\frac{d_1d_2}{4a}\)
где r — радиус вписанной окружности,
d1 и d2 — диагонали ромба,
a — сторона ромба,
Р — периметр ромба.
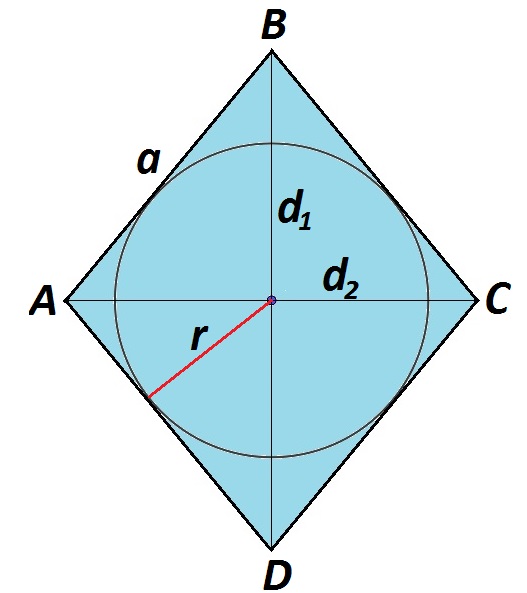
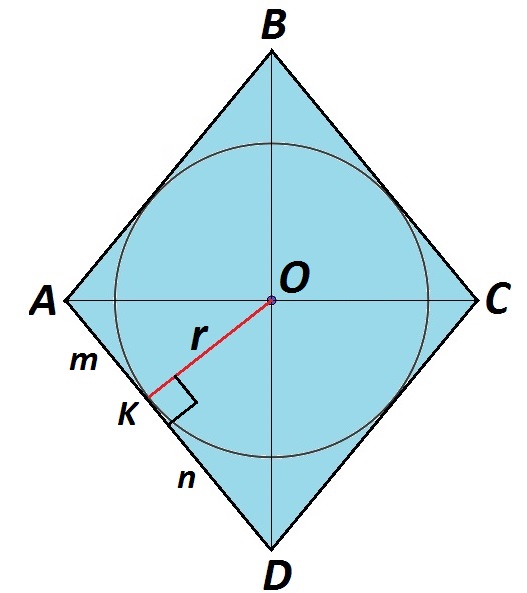
У изображенного ромба АВСD сторона равна а. Большая диагональ BD равна \(d_1\), меньшая диагональ АС равна \(d_2\). Радиус вписанной окружности:
\(r=\frac{d_1d_2}{4a}=\frac{BD\cdot AC}{4\cdot АВ}\).
Если известны только диагонали ромба
\(r=\frac{d_1d_2}{2\sqrt{\left(d_1\right)^2+\left(d_2\right)^2}}\)
где r — радиус вписанной окружности,
d1 и d2 — диагонали ромба.
Эту формулу можно получить из предыдущей.
Диагонали ромба пересекаются под прямым углом, делятся точкой пересечения пополам, и разбивают ромб на четыре прямоугольных треугольника.
Рассмотрим один из таких треугольников — ΔАВО. Сторона ромба АВ является гипотенузой ΔАВО.
Если известны диагонали ромба BD, равная \(d_1\) и АС, равная \(d_2\), то катеты ВО и АО ΔАВО будут равны \(\frac{d_1}2\) и \(\frac{d_2}2\) соответственно.
Выразим гипотенузу АВ треугольника АВО через его катеты ВО и АО.
Согласно теореме Пифагора \(АВ=\sqrt{ВО^2+АО^2}=\sqrt{\left(\frac{d_1}2\right)^2+\left(\frac{d_2}2\right)^2}\).
Подставив в формулу \(r=\frac{d_1d_2}p=\frac{d_1d_2}{4a}\) значение \(а=\sqrt{\left(\frac{d_1}2\right)^2+\left(\frac{d_2}2\right)^2}\) и упростив выражение,
получаем \(r=\frac{d_1d_2}{2\sqrt{\left(d_1\right)^2+\left(d_2\right)^2}}\).
Если известны сторона и угол
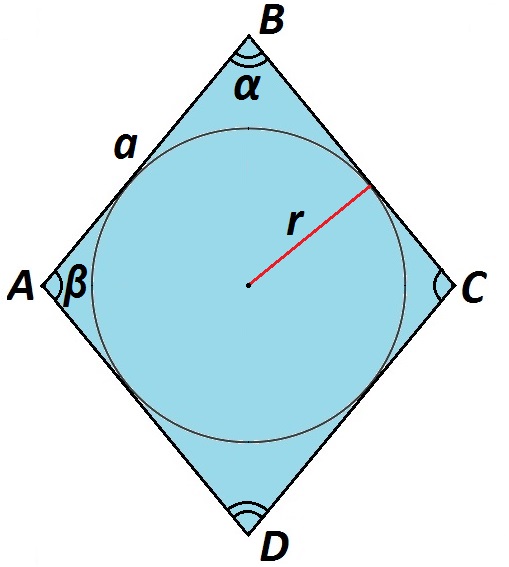
Радиус окружности, вписанной в ромб, равен половине произведения его стороны и синуса любого внутреннего угла ромба.
\(r=\frac{a\cdot\sin\alpha}2=\frac{a\cdot\sin\beta}2\)
где r — радиус вписанной окружности,
α и β — внутренние углы ромба,
a — сторона ромба.
Если известна высота ромба
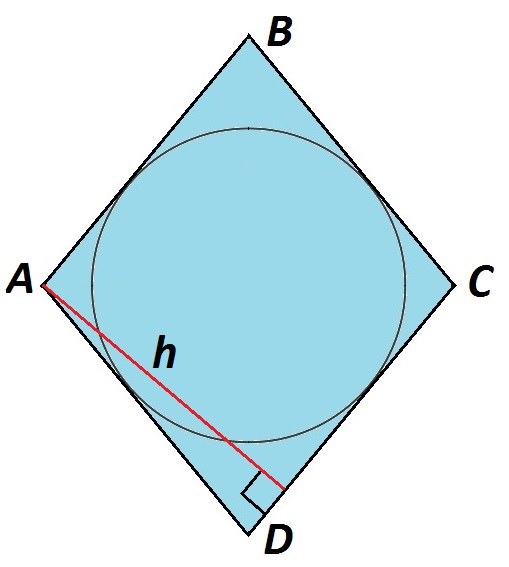
Радиус вписанной в ромб окружности равен половине его высоты.
\(r=\frac h2\)
где r — радиус вписанной окружности,
h — высота ромба.
Из этой формулы следует, что высота ромба равна диаметру вписанной в него окружности.
Если известны площадь ромба и его сторона
\(r=\frac S{2a}=\frac Sр\)
где r — радиус вписанной окружности,
S — площадь ромба,
a — сторона ромба,
р — полупериметр ромба.
Вычисление радиуса через отрезки m и n
Вписанная окружность касается стороны ромба. Точка касания делит сторону ромба на два отрезка. Пусть это будут отрезки m и n.
Диагонали ромба взаимно перпендикулярны, ΔАОD — прямоугольный. Высота ΔАОD к стороне АD равна радиусу вписанной в ромб АВСD окружности.
По свойству высоты прямоугольного треугольника, проведенной к гипотенузе, \(ОК=\sqrt{АК\cdot КD}\).
Следовательно, радиус вписанной в ромб окружности равен среднему пропорциональному между отрезками, на которые делит сторону ромба точка касания.
\(r=\sqrt{m\cdot n}\)
где r — радиус вписанной окружности,
m и n — отрезки, на которые делит сторону ромба точка касания.
Задачи с решениями
Дано: ромб с диагоналями 6 см и 8 см.
Найти: радиус вписанной в ромб окружности.
Решение: так как известны диагонали ромба,
применим формулу \(r=\frac{d_1d_2}{2\sqrt{\left(d_1\right)^2+\left(d_2\right)^2}}\).
\(r=\frac{6\cdot8}{2\sqrt{6^2+8^2}}=2,4 (см).\)
Ответ: радиус вписанной в ромб окружности равен 2,4 см.
Дано: ромб, сторона которого равна 16 см, а острый угол ромба — 30°.
Найти: радиус вписанной в ромб окружности.
Решение: применим формулу \(r=\frac{a\cdot\sin\alpha}2.\)
\(r=\frac{16\cdot0,5}2=\frac82=4 (см).\)
Ответ: радиус вписанной в ромб окружности равен 4 см.
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так