Определение расстояния между двумя параллельными прямыми

Как называется расстояние между двумя параллельными прямыми в пространстве

Две линии могут пересекаться или не иметь общих точек. Во втором случае прямые будут располагаться параллельно относительно друг друга. Для данного положения существует ряд характеристик, одной из которых является расстояние.

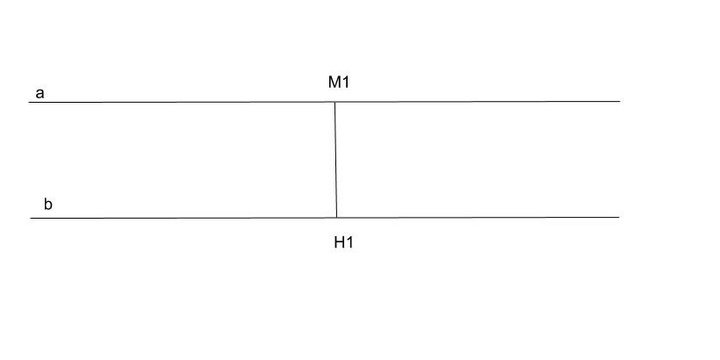
Схематично такие прямые можно представить следующим образом:

На рисунке представлен чертеж с двумя параллельными прямыми a и b. Точка М1 отмечена на прямой a. От нее можно опустить перпендикулярную линию к прямой b. Отрезок М1Н1 будет представлять расстояние между этими точками или параллельными линиями, на которых они расположены.

Доказательство теоремы, формула вычисления

Расстояние между двумя параллельными прямыми описывается теоремой. Звучит утверждение следующим образом: «На двух параллельных прямых все точки на одной из них равноудалены от точек, отмеченных на другой линии».

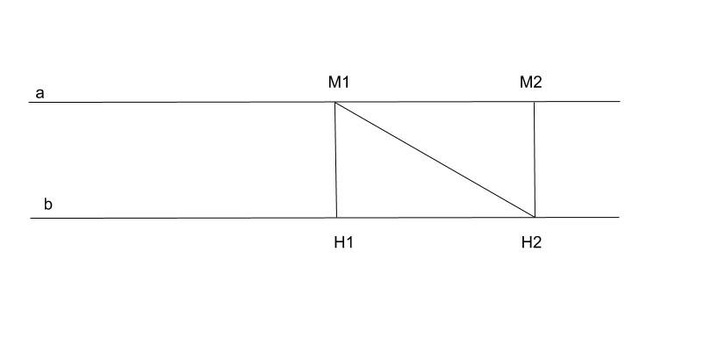
В качестве доказательства этой теории необходимо схематично представить две параллельные прямые линии a и b. На первой прямой можно отметить точку М1 и точку М2. С помощью перпендикуляров, пересекающих прямую b, можно отметить на ней аналогичные точки Н1 и Н2. Согласно определению расстояния между двумя параллельными прямыми, отрезок М1Н1 является расстоянием между прямой a и прямой b. Исходя из теоретического утверждения, необходимо доказать следующее отношение:

М1Н1 = М2Н2.

Схему можно дополнить с помощью некой секущей линии, которая представляет собой отрезок, пересекающий параллельные прямые. Исходя из условия параллельности двух прямых, можно заметить, что внутренние углы, образованные при пересечении секущей двух параллельных линий и лежащие накрест, равны друг другу. Таким образом:

угол М2М1Н2 = угол Н1Н2М1.

Согласно методике построения, отрезок М2Н2 перпендикулярен прямой b и расположен перпендикулярно к прямой a. Образованные в результате треугольники М1Н1Н2 и М2М1Н2 обладают прямыми углами и считаются равными по следующим характеристикам:

1. Общая гипотенуза М1Н2.
2. Равные острые углы М2М1Н2 и Н1Н2М1.

Исходя из утверждения, что у равных треугольников стороны также будут равны,

М1Н1 = М2Н2.

Таким образом, доказательства теоремы представлены.

Нахождение расстояния между параллельными прямыми

Определить удаленность двух линий, которые располагаются параллельно относительно друг друга, не составит труда. Достаточно измерить длину перпендикуляра, соединяющего две точки на этих прямых. Существует несколько способов, чтобы произвести данные вычисления:

• теорема Пифагора;
• признак равенства или подобия треугольников;
• метод координат в прямоугольной системе.

Подробнее следует рассмотреть последний способ. Если зафиксировать прямоугольную систему координат и задать в ней две параллельные линии a и b, то необходимо вычислить, насколько эти прямые удалены друг от друга. Решение задачи базируется на вычислении расстояния между этими линиями. Для этого необходимо выполнить следующие действия:

1. Определить координаты, соответствующие точке М1, отмеченной на одной из прямых линий.
2. Вычислить, каково расстояние от точки М1 до линии, к которой она не относится.

Исходя из примеров уравнений прямой на плоскости или в пространстве, можно достаточно просто вычислить координаты точки М1. Можно представить, что линия a соответствует следующему уравнению:

АХ + ВУ + С1 = 0

Пусть линия b соответствует такому уравнению:

АХ + ВУ + С2 = 0

Определить расстояние, на которое удалены эти параллельные прямые, можно по формуле:

\(\left|M1H1\right|=\frac{\left|C_{2}-C_{1} \right|}{\sqrt{A^{2}+B^{2}}}\)

Если выбрать какую-то точку М1(х1, у1) на прямой а, ее координаты будут соответствовать следующему уравнению:

Ах1 + Ву1 + С1 = 0.

В этом случае стоит отметить справедливость равенства:

Ах1 + Ву1 + С1 = 0, из которого получается следующая формула:

Ах1 + Ву1 = - С1.

В случае, если С2 меньше 0, то вид нормального уравнения прямой b будет следующим:

\(\frac{A}{\sqrt{A^{2}+B^{2}}}x+\frac{B}{\sqrt{A^{2}+B^{2}}}y+\frac{C_{2}}{\sqrt{A^{2}+B^{2}}}=0\)

Когда С2 равно либо больше 0, можно представить нормальное уравнение для прямой b таким образом:

\(\frac{A}{\sqrt{A^{2}+B^{2}}}x+\frac{B}{\sqrt{A^{2}+B^{2}}}y-\frac{C_{2}}{\sqrt{A^{2}+B^{2}}}=0\)

Найти расстояние между двумя параллельными прямыми, если С2 меньше 0, можно, используя такую формулу:

\(\left|M1H1\right|=\left| \frac{A}{\sqrt{A^{2}+B^{2}}}x_{1}+\frac{B}{\sqrt{A^{2}+B^{2}}}y_{1}+\frac{C_{2}}{\sqrt{A^{2}+B^{2}}}\right|\)

В случаях, когда С2 больше либо равно 0, расстояние вычисляется по следующей формуле:

\(\left|M1H1\right|=\left| -\frac{A}{\sqrt{A^{2}+B^{2}}}x_{1}-\frac{B}{\sqrt{A^{2}+B^{2}}}y_{1}-\frac{C_{2}}{\sqrt{A^{2}+B^{2}}}\right|=\left| \frac{A}{\sqrt{A^{2}+B^{2}}}x_{1}+\frac{B}{\sqrt{A^{2}+B^{2}}}y_{1}+\frac{C_{2}}{\sqrt{A^{2}+B^{2}}}\right|\)

В таком случае расстояние между двумя параллельными прямыми не зависит от величины С2 и определяется по формуле:

\(\left|M1H1\right|\)=\( \left| \frac{A}{\sqrt{A^{2}+B^{2}}}x_{1}+\frac{B}{\sqrt{A^{2}+B^{2}}}y_{1}+\frac{C_{2}}{\sqrt{A^{2}+B^{2}}}\right|\)

Следует применить формулу, полученную ранее:

\(Ах1 + Ву1 = - С1\)

Тогда окончательные расчеты будут выглядеть следующим образом:

\(\left|M1H1\right|=\left| \frac{-C_{1}}{\sqrt{A^{2}+B^{2}}}+\frac{C_{2}}{\sqrt{A^{2}+B^{2}}}\right|=\left| \frac{C_{2}-C_{1}}{\sqrt{A^{2}+B^{2}}}\right|\)

Таким образом, получилась формула, характерная для алгоритма метода координат. Данное уравнение можно применять для вычисления расстояние между двумя параллельными прямыми.

Примеры задач с решением

\(y=\frac{2}{3}x-1\)

\(\begin{cases} & \text{ if } x= 4+3*\lambda \\ & \text{ if } x= -5+2*\lambda \end{cases}\)

Решение

С помощью параметрических уравнений достаточно просто определить координаты точки, через которую проходит линия, соответствующая параметрическим уравнениям. Исходя из этих данных, получается:

точка М1 (4, -5).

Таким образом, необходимо рассчитать расстояние, на которое удалена точка М1 (4, -5) от прямой \(y=\frac{2}{3}x-1\)

Получение нормального уравнения прямой основано на преобразовании заданного уравнения прямой с угловым коэффициентом \(y=\frac{2}{3}x-1\). Выполнить это можно путем перехода к общему уравнению прямой:

\(y=\frac{2}{3}x-1\)

\(\frac{2}{3}x-1-y=0\)

2x – 3y – 3 = 0

Далее необходимо вычислить нормирующий множитель:

\(\frac{1}{\sqrt{2^{2}+(-3^{2})}}=\frac{1}{\sqrt{13}}\)

Полученный нормирующий множитель следует умножить на обе части последней формулы, чтобы в конечном итоге вывести формулу нормального уравнения прямой:

\(\frac{1}{\sqrt{13}}\times (2x-3y-3)=\frac{1}{\sqrt{13}}\times 0\)

\(\frac{2}{\sqrt{13}}x-\frac{3}{\sqrt{13}}y-\frac{3}{\sqrt{13}}=0\)

Расчет модуля значения крайнего равенства при условии, что х = 4, у = -5, позволит вычислить искомое расстояние между двумя параллельными прямыми:

\(\left|\frac{2}{\sqrt{13}}\times 4-\frac{3}{\sqrt{13}}\times (-5)-\frac{3}{\sqrt{13}} \right|= \frac{20}{\sqrt{13}}\)

Ответ: расстояние между двумя параллельными прямыми составляет \(\frac{20}{\sqrt{13}}\)

х – 3 = 0

\(\frac{x+5}{0}=\frac{y-1}{1}\)

Необходимо рассчитать расстояние, на которое две прямые отдалены друг от друга.

Решение

Исходя из условий задачи, в которых указано одно общее уравнение, выделим формулу для одной из исходных линий:

х – 3 = 0.

С помощью исходного канонического уравнения можно вычислить общую формулу:

\(\frac{x+5}{0}=\frac{y-1}{1}\)

х + 5 = 0

При переменной х наблюдается равенство коэффициентов в обоих уравнениях (также равны и при у — нулю). Исходя из данного условия, представляется возможным использовать формулу, чтобы вычислить расстояние, на которое удалены эти параллельные прямые друг от друга:

\(\left|M1H1 \right|=\frac{\left|C_{2}-C_{1} \right|}{\sqrt{A^{2}+B^{2}}}=\frac{\left|5-(-3) \right|}{\sqrt{1^{2}+0^{2}}}=8\)

Ответ: расстояние между двумя параллельными прямыми равно 8.