Нахождение кратчайшего расстояния между прямыми в пространстве
Что такое расстояние между прямыми в пространстве
Для начала дадим определение этому понятию.
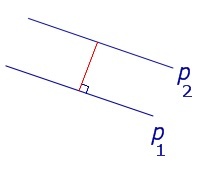
Расстояние между прямыми в пространстве — это отрезок, который соединяет две прямые линии по самому короткому пути. Иными словами, он перпендикулярен обеим этим прямым.
Но не всегда две линии могут быть параллельны друг другу.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
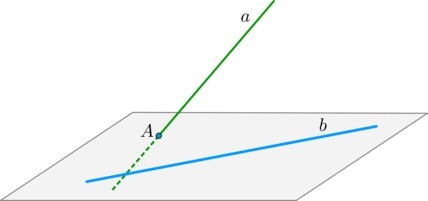
Расстояние между двумя скрещивающимися прямыми в пространстве — это расстояние между одной из скрещивающихся прямых и плоскостью, проходящей через вторую прямую параллельно первой.
Таким образом, чтобы найти расстояние между этими скрещивающимися прямыми, нужно от одной из прямых провести перпендикуляр на плоскость, в которой лежит другая прямая.
Между параллельными прямыми расстояние одинаково на протяжении всей их длины: перпендикуляр, опущенный из любой точки одной из этих линий, всегда будет одной и той же величины.
Метод координат для определения расстояния
Разберем пошагово способ определения расстояния между двумя скрещивающимися прямыми с помощью метода координат.
- Определить координаты точек \(М_1\) и \(М_2\), лежащих соответственно на прямых a и b.
- Найти x, y и z направляющих векторов для прямых a и b.
- Найти вектор-нормаль для плоскости, в которой лежит прямая b с помощью векторного произведения \(\overrightarrow a\) и \(\overrightarrow b\).
- Записать общее уравнение плоскости: \(A(x-x_0)+B(y-y_0)+C(z-z_0)=0\) и потом записать к нормированному виду уравнения плоскости, которое выглядит так: \(x\times\cos\left(\alpha\right)+y\times\cos\left(\beta\right)+z\times\cos\left(\gamma\right)-p=0\), где p — свободный член (число, которое равно расстоянию точки начала координат до плоскости), а \(\cos\left(\alpha\right),\;\cos\left(\beta\right)\) и \(\cos\left(\gamma\right)\) — координаты единичного нормального вектора плоскости.
- Далее, для определения расстояния от точки M до искомой плоскости, воспользуемся следующим уравнением: \(M_1H_1=\left|x_1\times\cos\left(\alpha\right)+y_1\times\cos\left(\beta\right)+z_1\cos\left(\gamma\right)-p\right|\), где \(x_1\), \(y_1\) и \(z_1\) — координаты точки \(M_1\), лежащей на прямой a, а \(H_1\) — точка, лежащая на искомой плоскости.
Примеры задач с решением
Задача 1
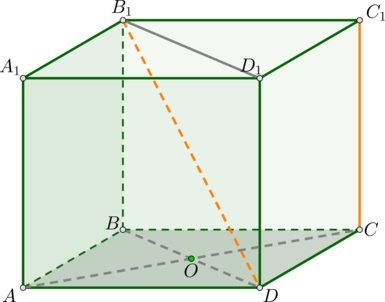
Дан куб \(ABCDA_1B_1C_1D_1\) с ребром равным \(\sqrt{32}\) см. Найти расстояние между прямыми \(DB_1\) и \(CC_1\).
Решение
Расстояние между скрещивающимися прямыми будем искать в качестве расстояния между прямой \(CC_1\) и плоскостью, проходящей через \(DB_1\) параллельно \(CC_1\). Так как \(DD_1\parallel CC_1\), плоскость \((B_1D_1D)\) параллельна \(СС_1\).
Сначала нужно доказать, что \(CO\) — перпендикуляр, проведенный к этой плоскости. \(CO\perp BD\) (как диагонали квадрата) и \(CO\perp DD_1\) (так как ребро \(DD_1\) перпендикулярно всей плоскости \((ABC)\)). Получается, \(CO\) перпендикулярен двум пересекающимся прямым из плоскости. Значит, \(CO\perp(B_1D_1D)\).
\(AC\) — диагонально квадрата — равна \(AB\sqrt2\), то есть \(AC=\sqrt{32}\times\sqrt2=\sqrt{64}=8\) см. Следовательно, \(CO=\frac12\times AC=4\) см.
Ответ: 4 см.
Задача 2
В трехмерном пространстве в прямоугольной системе координат Oxyz заданы две скрещивающиеся прямые a и b. Прямую a определяют параметрические уравнения прямой в пространстве:
\(\left\{\begin{array}{l}x=-2\\y=1+2\times\lambda\\z=4-3\times\lambda\end{array}\right.\)
А прямую b канонические уравнения прямой в пространстве:
\(\frac x1=\frac{y-1}{-2}=\frac{z+4}6\).
Вычислить расстояние между заданными прямыми.
Решение
Прямая a проходит через точку \(M_1(-2, 1, 4)\) и имеет направляющий вектор \(\overrightarrow a=(0, 2, -3)\). Прямая b проходит через точку \(M_2 (0, 1, -4)\), а ее направляющий вектором является вектор \(\overrightarrow b=(1, -2, 6)\).
Найдем векторное произведение векторов\( \overrightarrow a=(0, 2, -3)\) и \(\overrightarrow b=(1, -2, 6): \left[\overrightarrow a\times\overrightarrow b\right]=\begin{vmatrix}\overrightarrow i&\overrightarrow j&\overrightarrow k\\0&2&-3\\1&-2&6\end{vmatrix}=6\times\overrightarrow i-3\times\overrightarrow j-2\times\overrightarrow k\).
Так, \(\overrightarrow n=\left[\overrightarrow a\times\overrightarrow b\right]\) плоскости X, проходящей через прямую b параллельно прямой a, имеет координаты (6, -3, -2).
Таким образом, уравнение плоскости X есть уравнение плоскости, проходящей через точку \(M_2(0, 1, -4)\) и имеющей нормальный вектор \(\overrightarrow n=(6, -3, -2)\):
\(6\times(x-0)-3\times(y-1)-2\times(z-(-4))=0\;\leftrightarrow6x-3y-2z-5=0\)
Нормирующий множитель для общего уравнения плоскости \(6x-3y-2z-5=0\) равен \\(frac1{\sqrt{6^2+{(-3)}^2+{(-2)}^2}}=\frac17\). Значит, нормальное уравнение этой плоскости выглядит как \(\frac67x-\frac37y-\frac27z-\frac57=0\).
Воспользуемся формулой для вычисления расстояния от точки \(M_1(-2, 1, 4)\) до плоскости \(\frac67x-\frac37y-\frac27z-\frac57=0: \left|M\_1H\_1\right|=\left|\frac67\times(-2)-\frac37\times1-\frac27\times4-\frac57\right|=\left|\frac{-28}7\right|=4\) см.
Ответ: 4 см.
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так