Расстояние между точкой и плоскостью
Что такое расстояние от точки до плоскости
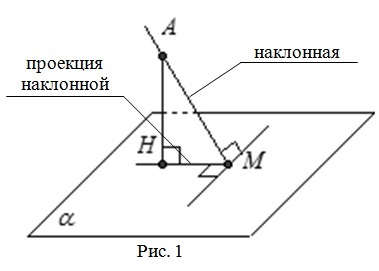
Расстоянием от точки до плоскости называют длину перпендикуляра, опущенного из точки на плоскость.
Рассмотрим плоскость \(\alpha\) и точку А, не принадлежащую этой плоскости. Проведем из точки А перпендикуляр к плоскости \(\alpha\), и обозначим буквой H точку пересечения этой прямой с плоскостью. Тогда отрезок АН является перпендикуляром, проведенным из точки А к плоскости \(\alpha\), а точка Н — основанием перпендикуляра. Поставим в плоскости \(\alpha\) произвольную точку М, различную с Н, и проведем отрезок AM. Этот отрезок называют наклонной, проведенной из точки А к плоскости \(\alpha\), а точка М основанием наклонной. Отрезок HM — проекция наклонной на плоскость \(\alpha\).
Рассмотрим прямоугольный треугольник АМН: сторона АН — катет, а сторона AM — гипотенуза, значит АН<АМ. Получаем, что, перпендикуляр проведенный из данной точки к плоскости, меньше любой наклонной, проведенной из той же точки к этой плоскости.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Следовательно, наименьшим из всех расстояний от точки А до различных точек плоскости \(\alpha\) будет расстояние до точки H, то есть отрезок АН. Это расстояние, т. е. длина перпендикуляра, проведенного из точки А к плоскости \(\alpha\), называется расстоянием от точки А до плоскости \(\alpha\).
С помощью этих рассуждений разберем следующую теорему.
Теорема о трех перпендикулярах
Прямая теорема
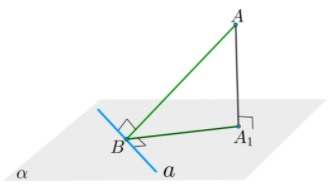
Если в плоскости провести прямую через основание наклонной перпендикулярно к ее проекции на данную плоскость, то эта прямая будет перпендикулярна и к самой наклонной.
Дано: \(AA_1\perp\alpha\), \(AB\) — наклонная, \(BA_1\) — проекция, \(a\subset\alpha\), \(a\perp BA_1\)
Доказать: \(a\perp AB\)
Доказательство:
- \(\left.\begin{array}{r}a\subset\alpha\\AA_1\perp\alpha\end{array}\right\}\Rightarrow AA_1\perp a\) (по определению прямой, перпендикулярной плоскости)
- \(\left.\begin{array}{r}a\perp AA_1\\a\perp A_1B\\AA_1,A_1B\subset(AA_1B)\\AA_1\cap A_1B\end{array}\right\}\Rightarrow a\perp(AA_1B)\) (по признаку перпендикулярности прямой и плоскости)
- \(\left.\begin{array}{r}a\perp(AA_1B)\\AB\subset(AA_1B)\end{array}\right\}\Rightarrow a\perp AB\) (по определению)
Обратная теорема
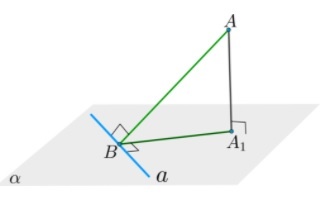
Если в плоскости провести прямую через основание наклонной перпендикулярно к ней, то эта прямая будет перпендикулярна и ее проекции.
Дано: \(a\perp AB\), \(AA_1\perp\alpha\), \(AB\) — наклонная, \(BA_1\) — проекция, \(a\subset\alpha\).
Доказать: \(a\perp A_1B\)
Доказательство:
- \(\left.\begin{array}{r}AA_1\perp\alpha\\A\subset\alpha\end{array}\right\}\Rightarrow AA_1\perp a\)
- \(\left.\begin{array}{r}a\perp AB\\a\perp AA_1\\AB,AA_1\subset(AA_1B)\\AB\cap AA_1\end{array}\right\}\Rightarrow a\perp(AA_1B)\)
- \(\left.\begin{array}{r}a\perp(AA_1B)\\A_1B\subset(AA_1B)\end{array}\right\}\Rightarrow a\perp A_1B\)
Задача
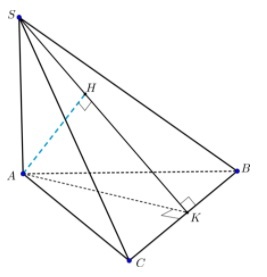
В тетраэдре SABC грани SAB и SAC — равные равнобедренные треугольники с прямыми углами при вершине А. Высота пирамиды равна h=BC. Найдите расстояние от точки А до грани SBC.
\(\triangle BAC\) равнобедренный, значит \(AK\perp BC\) и \(К\) — середина \(BC\). \(\triangle CSB\) так же равнобедренный, \(SK\perp BC\). Из этого следует, что точка Н отрезка AH (перпендикуляра на плоскость SBC) лежит на прямой SK. (что соответствует теореме о трех перпендикулярах: AH — перпендикуляр. HK — проекция, AK — наклонная)
\(\triangle SAC\) — прямоугольный и равнобедренный, \(SA=AC=h\), \(CK=\frac12BC=\frac h2\).
Тогда по теореме Пифагора в \(\triangle AKC\):
\(AK=\sqrt{h^2-\frac{h^2}4}=\sqrt{\frac{3h^2}4}=\frac{h\sqrt3}2\)
Рассмотрим прямоугольный \(\triangle SKA\):
\(SA=h, AK=\frac{h\sqrt3}2\), тогда \(tg\angle SKA=\frac{SA}{AK}=\frac h1:\frac{h\sqrt3}2=\frac2{\sqrt3}\).
Значит и в \(\triangle AHK\) \(\frac{AH}{HK}=\frac{2\sqrt3}3\).
Возьмем коэффициент x и получим уравнения:
\(AH=2\sqrt3x\), \(HK=3x\).
В \(\triangle AHK\) по теореме Пифагора:
\(x=\frac1{2\sqrt7}h\), значит \(AH=\sqrt{\frac37}h\)
Ответ: \(\sqrt{\frac37}h\)
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так