Разность квадратов

Что такое разность квадратов

a²−b²=(a+b)(a−b)

Важное условие:

a²−b²≠(a−b)²

Доказательство формулы разности квадратов

Арифметическое доказательство

Чтобы подтвердить справедливость определения разности квадратов, рассмотрим правую часть уравнения.

Раскроем скобки и получим:

(a+b)(a−b)=a²+ab−ba−b²=a²−b²

Справедливость формулы доказана.

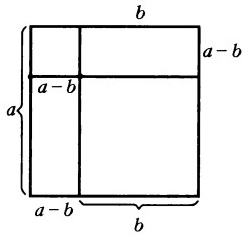
Геометрическое доказательство

Построим квадрат, сторона которого равна a, отсюда следует, что площадь S=a².

Далее начертим внутри имеющегося правильного четырехугольника квадрат со стороной b, следовательно площадь (S_b) данной фигуры будет равна b².

Продолжим любую прямую, на которой лежит сторона меньшего квадрата, до пересечения со стороной большего четырехугольника. В результате внутри исходного квадрата со стороной a имеем:

• квадрат со стороной b;
• прямоугольник, стороны которого равны а и (a−b);
• прямоугольник со сторонами b и (a−b).

Теперь найдем величину, которая останется при вычитание площади меньшего квадрата из площади большего. Как видим по чертежу, она равна площадям двух образовавшихся прямоугольников, то есть:

S_a−S_b=a(a−b)+b(a−b)=a²−ab+ba−b²=a²−b²

Формула доказана.

Применение формулы разности квадратов

Формула разности квадратов в алгебре может использоваться в двух видах случаев:

• при раскрытии скобок;
• при упрощении выражений.

Примеры прямого использования формулы и формулировка стандартной ошибки

Задача 1

Необходимо раскрыть скобки в выражении:

\(\left(15m-12n\right)\left(15m+12n\right)\)

Возьмем 15m в качестве a, 12n — в качестве b, значит:

\(\left(a-b\right)\left(a+b\right)\)

Исходя из формулы, запишем:

\(\left(a-b\right)\left(a+b\right)=a^2-b^2\)

Подставим в полученное выражение исходные переменные:

\(a^2-b^2=\left(15m\right)^2-\left(12n\right)^2=225m^2-144n^2\)

Стандартная ошибка прямого использования формулы заключается в следующем. Если в исходном выражении переместить в начало множитель со знаком плюс, при этом поменяв местами слагаемые, то получим:

\(\left(12n+15m\right)\left(15m-12n\right)\)

В данном варианте записи зачастую происходит путаница с уменьшаемым и вычитаемым, то есть: 

\(\left(12n+15m\right)\left(15m-12n\right)\neq\left(12n\right)^2+\left(15m\right)^2\)

Следует обратить внимание на множитель со знаком минус.

Задача 2

Раскройте скобки:

\(\left(4e+8f\right)\left(8f-4e\right)\)

Возьмем 8f за a, 4e за b, тогда: 

\(\left(4e+8f\right)\left(8f-4e\right)=\left(b+a\right)\left(a-b\right)\)

Учитывая возможность совершения стандартной ошибки при использовании формулы сокращенного умножения (разности квадратов), обращаем внимание на второй множитель, выраженный разностью. Чтобы применить формулу, нам необходимо поменять местами слагаемые в первом множителе. Тогда получим:

\(\left(a+b\right)\left(a-b\right)=a^2-b^2\)

Выполним подстановку исходных переменных:

\(\left(8f+4e\right)\left(8f-4e\right)=\left(8f\right)^2-\left(4e\right)^2=64f^2-16e^2\)

Задача 3

Упростите выражение:

\(\frac{36x^2-4}{6x+2}\)

Видим, что числитель раскладывается на множители по формуле разности квадратов:

\frac{36x^2-4}{6x+2}=\frac{\left(6x-2\right)\bcancel{\left(6x+2\right)}}{\bcancel{\left(6x+2\right)}}=\frac{\left(6x-2\right)}1=6x-2