Развернутый угол

Что такое развёрнутый угол — понятие и обозначение

Стороны развернутого угла взаимно дополняют друг друга. В результате получается прямая линия. Таким образом, стороны данной геометрической фигуры представляют собой дополнительные лучи. К примеру, на рисунке изображен ∠CDK, который является развернутым. Точка D служит его вершиной, лучи, обозначенные, как DK и DC – сторонами ∠CDK.

Решить задачу, в которой требуется начертить развернутый угол достаточно просто. Необходимо нарисовать прямую линию и поставить на ней отметку в виде точки, которая будет являться вершиной. Существует другой способ. В начале на плоскости отмечают произвольную точку. Данная отметка будет принята за вершину угла. Если через нее прочертить прямую линию, то получится развернутый угол. Схематично оба способа представлены на рисунке.

Определить, является ли угол развернутым, тупым или острым можно с помощью ряда признаков.

Основные свойства развернутого угла:

1. Стороны геометрической фигуры являются антипараллельными и складываются в прямую линию.
2. Развернутый угол в любом случае, независимо от способа начертания, будет составлять 180 градусов.
3. Если соединить вместе пару смежных углов, то полученная фигура будет выглядеть, как развернутый угол.
4. В случае, когда соединяют пару развернутых углов, в результате получают полный угол в 360 градусов, который равен сумме этих углов.
5. Прямой угол является половиной развернутого угла.

Геометрические фигуры с развернутыми углами

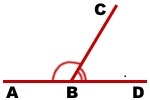
В геометрии производя некоторые манипуляции с развернутыми углами, можно получить новые фигуры. К примеру, если такую геометрическую фигуру разделить лучом на два угла, то полученные углы называют смежными. Такие элементы изображены на рисунке.

∠ABD  в данном случае является развернутым углом, а ВС представляет собой луч. Таким образом, углы ∠ABС и ∠CBD — смежные углы.

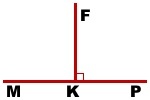
С помощью биссектрисы можно разделить представленную фигуру на два прямых угла. Наглядно данный метод получения геометрических фигур продемонстрирован на рисунке.

Так, согласно изображению, KF является биссектрисой развернутого ∠MKP. Полученные углы, ∠MKF и ∠FKP представляют собой прямые углы.

Какова градусная мера развернутого угла (сколько радиан)

Как и любой другой, развернутый угол можно измерить. Градусная величина геометрической фигуры будет составлять \(180^{0}\). Известно, что в данной единице меры укладывается 3,1415926… радиан. Так как длинные числа не всегда удобно использовать в расчетах, как правило, это число обозначают  буквой π. Таким образом, можно записать следующее справедливое обозначение:

\(180^{0}\approx 3,14\) радиан.

Точное отношение будет иметь следующий вид:

\(180^{0}=\pi\) радиан.

Примеры решения задач с развернутыми углами

Задача №1

Развернутый угол разделили с помощью луча на две части, которые являются аналогичными геометрическими фигурами. Градусные меры этих элементов относятся, как 1:4. Требуется найти полученные углы.

Решение

Следует обозначить искомые фигуры, как α и β. Предположим, что х является коэффициентом пропорциональности, тогда справедливы равенства:

α = х

β = 4х

Зная, что развернутый угол равен 180 градусам, что является суммой градусных мер углов, на которые он разбит с помощью луча, проходящего между его сторонами. Данное утверждение вытекает из свойств этой геометрической фигуры. Можно записать следующую формулу:

\(x+4x=180^{0}\Rightarrow 5x=180^{0}\)

Исходя из этого, можно определить углы:

\(x=\alpha =36^{0}\)

\(\beta =4x=4*36^{0}=144^{0}\)

Ответ: после разделения развернутого угла на две части один угол будет равен \(36^{0}\) второй ставит \(144^{0}\)

Задача 2

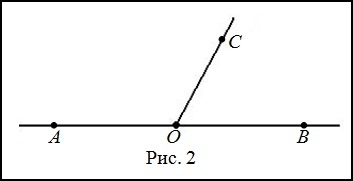
С помощью луча ОС развернутый угол, обозначенный, как АОВ, делят на два угла АОС и ВОС таким образом, что градусная мера угла АОС больше на 30 градусов, чем градусная мера угла ВОС. Требуется найти углы АОС и ВОС.

Решение

Условия задачи следует представить на рисунке:

Допустим, что ∠BOC = x, тогда, согласно условию задачи, получим следующее равенство:

∠AOC=(x+30)

Известно, что образованные углы являются смежными. Таким образом, в сумме эти углы будут составлять \(180^{0}\)

∠AOC+∠BOC=180          

В результате уравнение приобретает следующий вид:

\(x+x+30=180\Rightarrow 2x=150\Rightarrow x^{0}=75^{0}\)

∠BOC=75, откуда следует:

∠AOC=(x+30)=105

Ответ:  угол \(BOC=75^{0}\) угол \(AOC=105^{0}\)