Сфера и шар: формулы и свойства

Понятие сферы и шара

Если оглядеться вокруг, то можно найти множество шарообразных и сферических объектов в окружающем мире. Такая форма характерна для космических тел, в том числе, нашей планеты. С мячами разнообразных размеров, фактур и цветов люди встречаются во время занятий спортом и на игровых соревнованиях. Многие фрукты и овощи обладают круглой формой. Подобные примеры касаются реальной жизни. В рамках курса стереометрии перечисленные понятия отличаются. Важно уметь разбираться в терминологии и отличать фигуры друг от друга по ряду характерных признаков.

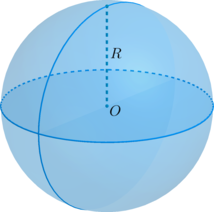
При рассмотрении вышеуказанных понятий часто встречается определение радиуса. Под ним подразумевают прямую, ограниченную парой точек, одна из которых лежит на сфере, а вторая — представляет собой центр этой фигуры. Кроме того, аналогичный отрезок играет роль радиуса шара, помещенного во внутреннее пространство анализируемой сферической фигуры. Наглядно представить эти понятия несложно, если обратиться к изображению, расположенному ниже на рисунке:

Источник: shkolkovo.net

Другое важное понятие касается диаметра сферы. Такое название присуще отрезку, пересекающему центральную точку сферической фигуры. При этом начало и конец данной линии расположены на рассматриваемой сфере. Непосредственно сфера является фрагментом шара. Существует аналогичное утверждение, когда окружность признают частью круга. Исходя из расшифровки термина сферы, можно сформулировать справедливое заключение о равенстве радиусов этой фигуры.

Таким образом, центральная точка сферической фигуры делит диаметр пополам. В свою очередь, диаметр сферы в два раза превышает размер радиуса аналогичного объекта. Кроме того, сфера представляет собой тело вращения. Из данного определения можно сделать вывод о способе получения сферической фигуры. Достаточно лишь повернуть половину окружности относительно ее диаметра, чтобы образовалась сфера.

Свойства

Из курса геометрии известно, что при решении задач на вычисление параметров или начертание разнообразных фигур целесообразно использовать их свойства. В случае со сферическими объектами этот метод не менее эффективен. Сфера обладает рядом специфических свойств, знание которых значительно упрощает и ускоряет решение многих примеров из стереометрии. Перечислим основные из них:

1. Какое-либо сечение шара с помощью плоскости позволяет получить геометрическую фигуру в виде круга.
2. Какое-либо сечение шарообразного предмета, выполненное посредством некоторой плоскости, имеет круглую форму.
3. При выборе любого сечения сферического объекта в результате получается окружность.
4. Каждая из точек, принадлежащих сфере, находится на одинаковом расстоянии от ее центральной точки.
5. Сфера обладает максимальным объемом по сравнению с прочими фигурами в пространственном измерении, которые характеризуются идентичными поверхностными площадями.
6. Через пару произвольных диаметрально противоположных точек, которые расположены на наибольшем удалении друг от друга и принадлежат одной окружности, допустимо построить любое число кругов для шара или окружностей для сфер радиусом, соответствующим радиусу рассматриваемого шара или сферы.

Формулы площади и объема с доказательством

Как и в случае любых геометрических форм, для сферы и шара предусмотрены формулы, с помощью которых можно вычислить их параметры. Подобные математические соотношения полезны при решении задач по стереометрии. Зная величину радиуса или диаметра объекта, несложно рассчитать его площадь и объем. Рассмотрим такие выражения и докажем, что они являются справедливыми равенствами.

\(S=\ 4\pi r^{2}\)

\(S=\ \pi d^{2}\)

\(V={\frac {4}{3}}\pi r^{3}\)

Необходимо подтвердить корректность записанных равенств. С этой целью следует выделить одну четвертую часть от круга, радиус которого равен R, а его центральная точка совпадает с точкой, имеющей координаты \(\left(0;0\right)\). Запишем уравнение окружности, применимое для рассматриваемого случая:

\(x^{2}+y^{2}=R^{2}\)

В результате получим, что:

\(y^{2}=R^{2}-x^{2}\)

Заметим, что функция \(y={\sqrt {R^{2}-x^{2}}},x\in (0;R)\) не прерывается, убывает и не является отрицательной. В процессе вращательного движения четвертая часть круга относительно оси абсцисс формирует некий полушар. Исходя из этого, допустимо составить следующее равенство:

\({1 \over 2}V=\pi \int \limits _{0}^{R}(R^{2}-x^{2})dx=\pi \cdot {\Bigl .}\left(R^{2}x-{\frac {x^{3}}{3}}\right){\Bigr |}_{0}^{R}=\pi \cdot (R^{3}-{\frac {R^{3}}{3}})={\frac {2}{3}}\pi R^{3}\)

Таким образом, получим исходное соотношение:

\(V={\frac {4}{3}}\pi R^{3}\)

Путем нескольких несложных математических преобразований удалось доказать справедливость записанных формул. Далее также в некоторое количество действий допустимо подтвердить справедливость следующего выражения:

\(V={\frac {\pi d^{3}}{6}}\)

Доказательство:

\(d=2r, V={4 \over 3} \pi r^3 = {4 \over 3} \pi \left ( {d \over 2} \right )^3 = {4 \over 3} \pi \frac {d^3} {8} = \frac {\pi d^3} {6}\)

Примеры решения задач

Решение

При известном радиусе и объеме шара достаточно просто определить значение поверхностной площади заданной фигуры. С этой целью нужно вспомнить соответствующие формулы из курса теории. Применим эти уравнения к условиям задачи и выполним необходимые вычисления:

\(V_{\text{шара}} = \frac{4}{3}\pi R^3 = \frac{36}{\sqrt\pi} \Rightarrow R = \frac{3}{\sqrt\pi}\)

Найдем радиус полученного шара:

\(R_{\text{нов.}} = R + \frac{6}{\sqrt\pi} = \frac{9}{\sqrt\pi}\)

Далее остается лишь путем подстановки найденных значений в стандартную формулу определить искомую площадь поверхности:

\(S_{\text{пов.}} = 4\pi R_{\text{нов.}}^2 = 4\pi \left(\frac{9}{\sqrt\pi}\right)^2 = 4\pi\frac{81}{\pi} = 324\)

Ответ: \(S_{\text{пов.}} = 324\)

 

Решение

В процессе решения задачи потребуется найти частное от деления объема шара на объем обозначенного в условии сегмента. Высоту рассматриваемого фрагмента допустимо выразить с помощью следующего уравнения:

\(H = \frac{1}{2}R\)

Далее воспользуется стандартными формулами, знакомыми из теоретического курса стереометрии, и выполним соответствующие расчеты:

\(\frac{V_{\text{шара}}}{V_{\text{сегм.}}} = \frac{\frac{4}{3}\pi R^3}{\pi \left(\frac{1}{2}R\right)^2\left(R - \frac{1}{3}\left(\frac{1}{2}R\right)\right)} = \frac{\frac{4}{3}\pi R^3}{\frac{5}{24}\pi R^3} = \frac{4}{3} \cdot \frac{24}{5} = \frac{32}{5} = 6,4\)

Ответ: 6,4

Источник: shkolkovo.net

Решение

Представим, что \(V_1\) представляет собой объем шарообразной фигуры, которая ограничена первой сферой. Исходя из того, что радиус \(S_1\) в два раза превышает значение радиуса \(S_2\), целесообразно записать следующее соотношение:

\(V_1 : V_2 = 8\)

Таким образом:

\(V = V_1 - V_2 = 8V_2 - V_2 = 7V_2\)

В результате получим:

\(V : V_2 = 7\)

Ответ: 7.