Чему равна сумма углов треугольника
Теорема о сумме углов треугольника: сумма углов треугольника равна 180о
Доказательство
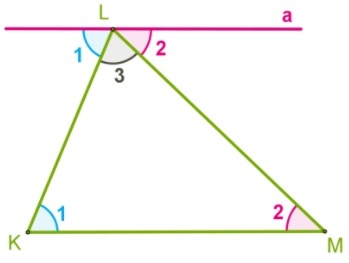
Докажем, что в \(\triangle KLM\) \(\angle K+\angle L+\angle M=180^\circ\)
Через вершину L проведем прямую а, параллельную KM.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Углы, обозначенные цифрой 1 — накрест лежащие при \(а\parallel KМ\) и секущей KL. То есть они равные, как и углы, обозначенные цифрой 2 — накрест лежащие при а\parallel KМ и секущей МL.
Тогда \(\angle1+\angle2+\angle3=180^\circ\) т.к. составляют развернутый угол при вершине L.
Теорема доказана.
Следствия
- Сумма острых углов прямоугольного треугольника равна \(90^\circ\) (т.к. в прямоугольном треугольнике один из углов прямой, сумма двух других равна \(180^\circ-90^\circ=90^\circ\)).
- В равнобедренном прямоугольном треугольнике каждый острый угол равен величине \(45^\circ\).
- В равностороннем треугольнике все углы равны \(60^\circ\).
- В любом треугольнике либо все углы острые, либо два угла острые, а третий — тупой или 90 градусов.
- Внешний угол треугольника равен сумме двух его углов, не смежных с ним.
Теорема о сумме углов для прямоугольного треугольника
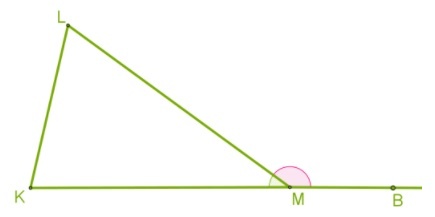
Внешний угол треугольника равен сумме двух его углов, не смежных с ним.
\(\angle KML+\angle BML=180^\circ\) (смежные)
\(\angle K+\angle L+\angle KML=180^\circ\)
Значит, \(\angle BML=\angle K+\angle L\)
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так