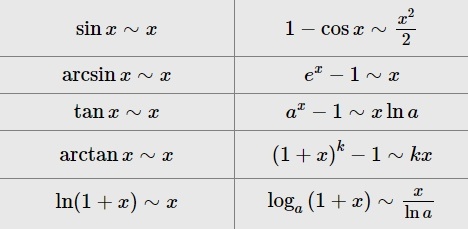Эквивалентные функции

Что такое эквивалентные функции

Эквивалентные функции позволяют облегчить процесс вычисления пределов с помощью замены множителей в примерах с дробями и произведениями.

Функции α(x) и β(x) называются эквивалентными при x→α, если $\lim_{x\rightarrow\alpha}\frac{\alpha(x)}{\beta(x)}=1.$

Данное определение применимо к бесконечно большим и малым функциям.

Эквивалентность обозначается знаком ∼, т.е. чтобы показать, что функции α(x) и β(x) эквивалентны, нужно оформить запись следующим образом: α(x)∼β(x)

Для удобства следует использовать специальную таблицу.

Эквивалентные функции и их применение к нахождению пределов

Свойства функций

Основные свойства бесконечно малых функций:

1. $\alpha\sim\alpha,\;(\lim_{x\rightarrow a})\frac\alpha\alpha=1.$
2. Если $\alpha\sim\beta и \beta\sim\gamma, то \alpha\sim\gamma,\;(\lim_{x\rightarrow\alpha}\frac\alpha\gamma=\lim_{x\rightarrow\alpha}(\frac\alpha\beta\times\frac\beta\gamma)=1\times1=1).$
3. Если $\alpha\sim\beta и \beta\sim\gamma и \beta\sim\gamma, то (\lim_{x\rightarrow\alpha}\frac\beta\alpha=\lim_{x\rightarrow\alpha}\frac1{\displaystyle\frac\alpha\beta}=1).$
4. Если $\alpha\sim\alpha_1 и \beta\sim\beta и \lim_{x\rightarrow\alpha}\frac\alpha\beta=\kappa, то и \lim_{x\rightarrow\alpha}\frac{\alpha_1}{\beta_1}=\kappa или \lim_{x\rightarrow\alpha}\frac\alpha\beta=\lim_{x\rightarrow\alpha}\frac{\alpha_1}{\beta_1}.$

Основные свойства эквивалентных бесконечно больших функций:

1. $\frac{\alpha(x)-\beta(x)}{\alpha(x)}=(1-\frac{\beta(x)}{\alpha(x)})\overset{x-\alpha}{\rightarrow0}.$
2. $x = {-b \pm \sqrt{b^2-4ac} \over 2a}\alpha(x)\sim\lambda\beta(x), где \lambda=\lim_{x\rightarrow\alpha}\frac{\alpha(x)}{\beta(x)}.$
3. $\alpha(x)+\beta(x)\sim\alpha(x).$

Применяемые определения 

Основные определения:

1. Функции $\alpha(x) и \beta(x)$ бесконечно малы при $x\rightarrow\alpha.$
2. Если есть $\lim_{x\rightarrow\alpha}\frac{\alpha(x)}{\beta(x)}=C\neq0,\;\infty, то \alpha(x) и \beta(x)$ бесконечно малые одного и того же порядка при $x\rightarrow\alpha$ 
3. Если есть $\lim_{x\rightarrow\alpha}\frac{\alpha(x)}{\beta(x)}=0$ , то $\alpha(x)$— величина более высокого порядка малости, чем $\beta(x)$ при $x\rightarrow\alpha.$
4. Если $\not\ni\lim_{x\rightarrow\alpha}\frac{\alpha(x)}{\beta(x)}$, то бесконечно малые $\alpha(x) и \beta(x)$ несравнимы при $x\rightarrow\alpha.$
5. Суммой двух бесконечно больших функций при $x\rightarrow\alpha$ является неопределенность.
6. Произведением бесконечно большой функции и функции, имеющей в точке α конечный ненулевой предел, является бесконечно большая функция при $x\rightarrow\alpha.$

Данных определений будет достаточно для решения пределов с применением понятия эквивалентности.

Применяемые теоремы

Теорема 1 (о замене эквивалентными в произведении и отношении):

Если $\alpha_1(x),\;\alpha_2(x),\;\beta_1(x),\;\beta_2(x)$ являются бесконечно малыми при $x\rightarrow\alpha и \alpha_1(x)\sim\beta_1(x),\;\alpha_2(x)\sim\beta_2(x)$ при $x\rightarrow\alpha$, то

• $\alpha_1(x)\times\alpha_2(x)\sim\beta_1(x)\times\beta_2(x);$
• $\frac{\alpha_1(x)}{\alpha_2(x)}\sim\frac{\beta_1(x)}{\beta_2(x)}$ при $x\rightarrow\alpha;$
• $\lim_{x\rightarrow\alpha}\frac{\alpha_1(x)}{\alpha_2(x)}=\lim_{x\rightarrow\alpha}\frac{\beta_1(x)}{\beta_2(x)}.$

Теорема 2:

Для того чтобы бесконечно малые функции α(x) и β(x) были эквивалентными при $x\rightarrow\alpha$, нужно, чтобы при $x\rightarrow\alpha$ выполнялось любое из равенств:

• $\alpha(x)-\beta(x)=\circ(\alpha(x));$
• $\alpha(x)-\beta(x)=\circ(\beta(x)).$

Теорема 3:

Разность двух эквивалентных бесконечно малых функций есть бесконечно малая функция более высокого порядка, чем каждая из них.

Верно и обратное утверждение.

Теорема 4:

Сумма конечного числа бесконечно малых функций разных порядков эквивалентна слагаемому низшего порядка.

Теорема 5 (о замене эквивалентных функций в пределах частного):

Если при $x\rightarrow x_0, \alpha(x)\sim\alpha_1(x), \beta(x)\sim\beta_1(x)$ существует предел $\lim_{x\rightarrow x_0}\frac{a_1(x)}{\beta_1(x)},$ то существует и предел $\lim_{x\rightarrow x_0}\frac{a(x)}{\beta(x)}=\lim_{x\rightarrow x_0}\frac{a_1(x)}{\beta_1(x)}.$

Сравнение функций

Сравнение бесконечно малых функций

1. Если $\lim_{x\rightarrow\alpha}\frac{a(x)}{\beta(x)}$ есть конечное ненулевое число, то $\alpha(x)$ и $\beta(x)$ называются бесконечно малыми одного и того же порядка.
2. Если $\lim_{x\rightarrow\alpha}\frac{a(x)}{\beta(x)}$ есть ноль, то $\alpha(x)$ по сравнению с $\beta(x)$ является бесконечно малой более высокого порядка при $x\rightarrow\alpha$, а $\beta(x)$ по сравнению с $\alpha(x)$— бесконечно малой меньшего порядка.
3. Если $\lim_{x\rightarrow\alpha}\frac{a(x)}{\beta(x)}$ есть бесконечность, то $\beta(x)$ по сравнению с $\alpha(x)$ является бесконечно малой более высокого порядка при $x\rightarrow\alpha$, а $\alpha(x)$ по сравнению с $\beta(x)$ — бесконечно малой меньшего порядка.

Сравнение бесконечно больших функций

1. Если $\lim_{x\rightarrow\alpha}\frac{a(x)}{\beta(x)}$ больше нуля и меньше бесконечности, то $\alpha(x)$ и $\beta(x)$ называются бесконечно большими одного и того же порядка.
2. Если $\lim_{x\rightarrow\alpha}\frac{a(x)}{\beta(x)}$ есть бесконечность, то $\alpha(x)$ по сравнению с $\beta(x)$ является бесконечно большой более высокого порядка, при $x\rightarrow\alpha$. При этом $\beta(x)$ имеет меньший порядок роста.
3. Если $\lim_{x\rightarrow\alpha}\frac{a(x)}{\beta(x)}$ есть ноль, то $\beta(x)$ по сравнению с $\alpha(x)$ является бесконечно большой более высокого порядка при $x\rightarrow\alpha.$
4. Если $\alpha(x) и \beta^n(x)$ являются бесконечно большими функциями одного и того же порядка, то функция $\alpha(x)$ по сравнению с $\beta^n(x)$ называется бесконечно большой n-ного порядка.

Примеры решения пределов с помощью эквивалентных функций

Пример 1

Найти предел:

$\lim_{x\rightarrow0}\frac{\ln\left(1+4x\right)}{\sin\left(3x\right)}$

Решение

Воспользуемся таблицей эквивалентных функций. 

$\ln\left(1+\alpha\right)\sim\alpha,\;\sin\left(\alpha\right)\sim\alpha$

Следовательно,

$lim_{x\rightarrow0}\frac{\ln\left(1+4x\right)}{\sin\left(3x\right)}=\lim_{x\rightarrow0}\frac{4x}{3x}=\frac43$

Пример 2

Найти предел:

$\lim_{x\rightarrow0}\frac{\sqrt[3]{1+x}-1}x$

Решение

Воспользуемся таблицей эквивалентных функций.

$\sqrt[3]{1+x}\sim1+\frac x3$

Следовательно,

$\lim_{x\rightarrow0}\frac{\sqrt[3]{1+x}-1}x=\lim_{x\rightarrow0}\frac{{(1+x)}^{\displaystyle\frac13}-1}x=\lim_{x\rightarrow0}\frac{1+{\displaystyle\frac x3}-1}x=\frac13\lim_{x\rightarrow0}\frac xx=\frac13$

Пример 3

Найти предел:

$\lim_{x\rightarrow\mathrm\pi}\frac{1+\cos\left(x\right)}{{(x-\mathrm\pi)}^2}$

Решение

Произведем замену переменной

 $(x-\mathrm\pi)=y, где y\rightarrow0, если x\rightarrow\mathrm\pi$

Преобразуем выражение.

$L=\lim_{x\rightarrow\mathrm\pi}\frac{1+\cos\left(x\right)}{{(x-\mathrm\pi)}^2}=\lim_{y\rightarrow0}\frac{1+\cos\left(y+\mathrm\pi\right)}{y^2}$

Применим формулу приведения:

$\cos\left(y+\mathrm\pi\right)=-\cos\left(y\right)$

Получим:

$L=\lim_{y\rightarrow0}\frac{1-\cos\left(y\right)}{y^2}$

Воспользуемся таблицей эквивалентных функций.

$1-\cos\left(y\right)\sim\frac{y^2}2$

Следовательно,

$L=\lim_{y\rightarrow0}\frac{1-\cos\left(y\right)}{y^2}=\lim_{y\rightarrow0}\frac{\displaystyle\frac{y^2}2}{y^2}=\frac12$