Синус бесконечности

Что такое Синус (sin) бесконечности

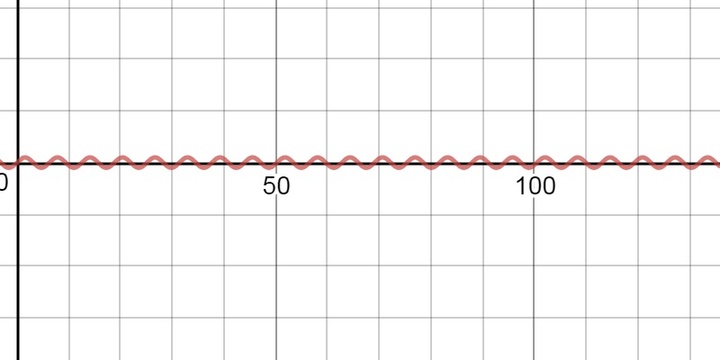
Известно, что sin(x) имеет любое значение в пределах [-1, 1]. Когда указывается, что x стремится к бесконечности, это означает, что x увеличивается. Изобразив это графически, мы увидим колеблющийся ряд, где \(-1\leqslant x\leqslant1\).

\(x \mapsto ∞ \\\) не приближается к какому-либо фиксированному значению y.

Колеблющиеся значения синуса означают, что для каждого действительного числа R существуют числа x, y⩾R, такие что sin (x) = 1 и что sin (y) = -1.

Предел тригонометрической функции

Неопределенность предела синуса на бесконечности доказывается через тригонометрическую функцию. Допустим, что существует некий предел выражения:

\(\lim_{n\rightarrow\infty}\sin\left(n\right)\)

Этот предел предполагает, что выражение стремится к какой-то конечной величине на бесконечности. Тогда справедливо следующее условие:

\(\lim_{n\rightarrow\infty}\sin\left((n+1\right)\;-\;\sin\left(n-1\right))\;=\;0\)

Далее разложим синусы по соответствующему правилу, получим:

\(\sin\left(\alpha\right)-\sin\left(\beta\right)=2\cos\left(\frac{\alpha+\beta}2\right)\;\cdot\sin\left(\frac{\alpha-\beta}2\right)\)

Из этого следует, что 

\(\lim_{n\rightarrow\infty}2\cos\left(n\right)\sin\left(1\right)\;=\;0, то есть \lim_{n\rightarrow\infty}\cos\left(n\right)\;=\;0\)

Тогда предел \(\sin\left(2n\right) при n\;\rightarrow\;\infty\) тоже равен нулю:

\(\lim_{n\rightarrow\infty}\sin\left(2n\right)\;=\;2\sin\left(n\right)\cos\left(n\right)\;=\;0\)

Требование к выполнению тригонометрического тождества

При решении тригонометрической функции необходимо соблюдать основное тригонометрическое тождество, определяющее связь между косинусом и синусом угла.

\(\sin^2n+cos^2n=1 \)

Результат решения уравнения

Исходя из вышеописанного, если \(\lim_{n\rightarrow\infty}\sin\left(n\right)\) существует, то будет применимо условие \(\lim\;\sin\left(n\right)=0\)

Но тогда cos(n) должен стремиться к нулю, а sin(n) к единице. Подобное заключение не соответствует здравому смыслу. Следовательно, доказано, что для синуса предел на бесконечности не определяется.