Правила сложения и вычитания натуральных чисел
Что такое натуральные числа
Много ситуаций вокруг нас связано с действиями с натуральными числами. Каждое из них можно представить шагами на обычной школьной линейке с нанесенными делениями, числовой прямой и координатном луче. В результате сложения исходное натуральное число увеличивается, а в результате вычитания — уменьшается. Для таких математических действий также существуют законы, которые будут рассмотрены ниже.
Понятие натурального числа обусловлено необходимостью естественного счета предметов и расположения цифр друг относительно друга. Множество таких чисел характеризуется бесконечностью. На деле это выглядит так: относительно любого числа есть еще одно, которое на единицу больше. Если расположить эти числа в порядке возрастания, получится натуральный ряд – еще одно математическое понятие, связанное с натуральными числами. Примером такого ряда является обычная линейка. В то же время необходимо понимать, что линейка имеет последнее число (например, линейка на 30 см ограничивается числом 30, а на 40 см — 40). В отличие от обычной линейки, числовая прямая не имеет крайнего числа, как показано на рисунке:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Источник: mathematics-tests.com
Представляя натуральные числа в виде числовой прямой, необходимо также помнить, что натуральным рядом является только множество целых чисел, причем имеющих знак «+». Если на прямой нанесены числа, расположенные слева от нуля, то этот ряд не является натуральным. Поэтому в математике говорят о расположении натуральных чисел на луче.
Расположение чисел на луче помогает представить действия с натуральными числами:
- продвинувшись на несколько делений вправо, число получает увеличение на число таких шагов;
- если переместиться на несколько шагов влево, получается результат, равный действию вычитания из исходного числа количества геометрических шагов.
Геометрическим шагом называется единица, на которую совершается геометрическое действие.
Источник: prezentacii.org
На данном рисунке шагом является любой отрезок между двумя соседними натуральными числами.
Все натуральные числа можно назвать их множеством. Для обозначения такого множества определена буква латинского алфавита N.
В математике для множества натуральных чисел существуют следующие правила:
- Единица является наименьшим натуральным числом.
- При фоне существования наименьшего числа отсутствует наибольшее.
- При сравнении каждого последующего числа с предыдущим, обязательное условие — их разница на единицу. Другими словами, каждый последующий участник ряда больше предыдущего на один.
Законы сложения натуральных чисел
Зная особенности натурального ряда, можно выполнить задание по определению неизвестного числа. Например, числом, следующим за тройкой, является четыре, а следующим за числом 25, является 26.
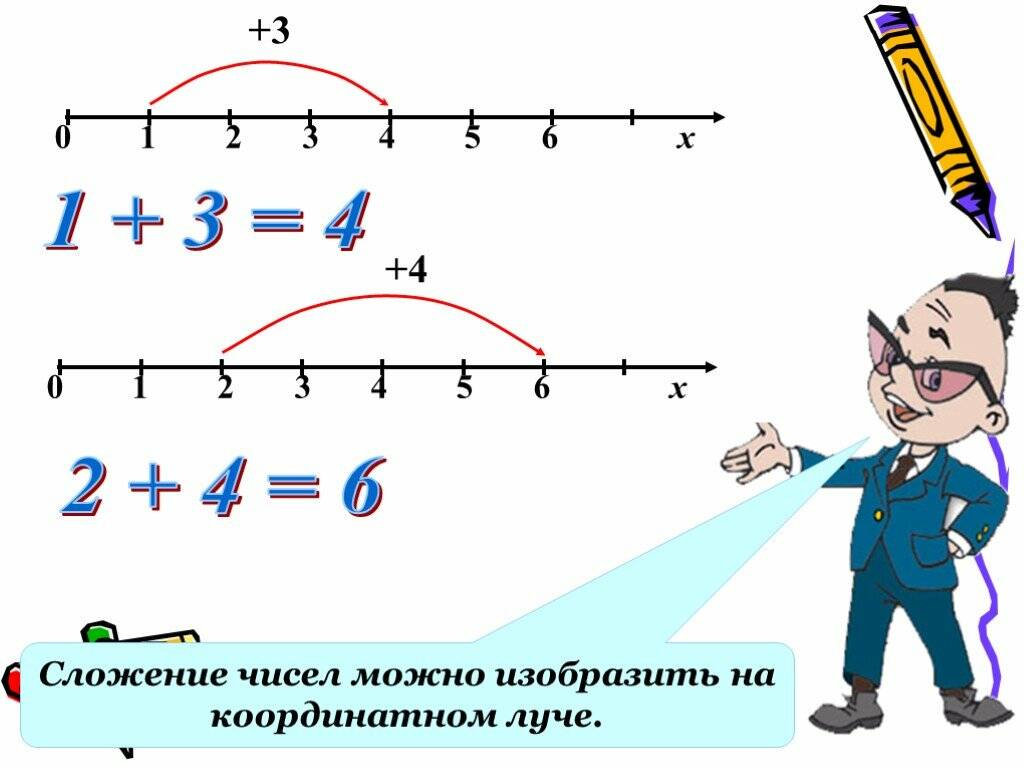
Используя такое свойство, можно складывать два натуральных числа. Так, если нужно к трем прибавить два, значит, следует передвинуться на два шага вправо. Получится пять.
Аналогичный способ приемлем для сложения чисел, которые могут быть разложены на небольшое количество единиц. Для иных случаев он очень не удобен. Увеличение числа поединично занимает много времени.
Вторым вариантом сложения является определение суммы единиц, которые составляют оба числа.
Если необходимо сложить два числа, они превращаются в слагаемые. Их может быть несколько. Последовательность сложения может быть различной, но в результате обязательно получается число, которое в математике называется суммой.
Источник: fsd.multiurok.ru
Из данного действие вытекает определение математического действия.
Математическое действие — способ нахождения нового числа с использованием двух или нескольких имеющихся.
При этом не только сложение является математическим действием. Ведь не всегда требуется найти число в результате прибавления к нему другого числа. Задача может заключаться в уменьшении имеющегося на определенную величину.
Вычитание натуральных чисел
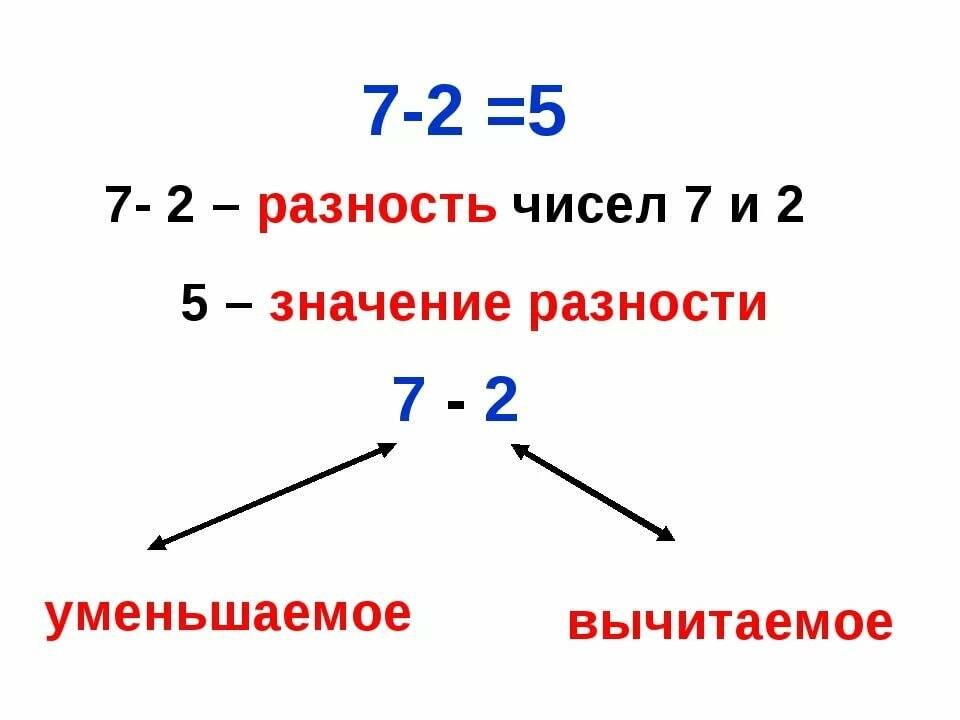
Аналогично сложению выполняется вычитание — действие, которое заключается в уменьшении первого числа на величину второго. При этом первое называется уменьшаемым, второе — вычитаемым, а полученный результат — разностью.
Источник: heaclub.ru
Рассмотрим действие вычитания на схеме с лучами.
Источник: prezentacii.org
На первом луче от имеющегося числа 7 необходимо вычесть 3. Сделав поочередно три шага влево по лучу, можно определить разность в этом действии. Она равна четырем.
На втором координатном луче аналогично произведено действие вычитания из шести четыре. Разность — два.
Умение вычесть из одного числа другое пригодится в решении задач по нахождению одного из слагаемых при известной сумме. Так, например, зная, что сумма двух чисел равна 7, а один из слагаемых трем, можно найти второе слагаемое. Для этого производим действие вычитания:
7-3=4
Разность в данном примере составляет 4.
Действие по вычитанию натуральных чисел может происходить в том случае, когда вычитаемое меньше уменьшаемого. В противном случае в результате получится отрицательное число, которое не является натуральным.
Свойства сложения и вычитания натуральных чисел
При решении задач на сложение и вычитание натуральных чисел важно грамотно использовать свойства этих действий.
К ним относятся:
- Переместительное свойство.
Для понимания рассмотрим пример. На ветке сидело 5 воробьев. К ним прилетело еще трое. Сколько воробьев в результате сидит на ветке? Произведя действие по сложению, получаем:
5+3=8
Данную задачу можно сформулировать и по другому, а именно: На ветке сидело трое воробьев. К ним прилетело еще пятеро. Сколько всего воробьев? Теперь прибавляем к трем пять. В результате — та же сумма. 8.
Следовательно, можно поменять местами слагаемые, от чего сумма не изменится. Данное свойство формулируется следующим образом: от перемены мест слагаемых сумма не меняется.
Переместительное свойство можно использовать для облегчения устного счета. Так, если к 9 нужно добавить 23, это устно сделать затруднительно. Гораздо проще представить действие, когда к 23 прибавить 9. В итоге сумма равна 32.
Переместительное свойство справедливо только для сложения. В вычитании оно не работает.
- Сочетательное свойство.
Упростить сложение с помощью сочетательного свойства также легко. Если к имеющемуся числу нужно добавить сумму двух чисел, то можно выбрать, какое из них прибавлять первым. В таком случае действие рассматривается как нахождение суммы первого числа с одним из пары добавляемых чисел, с последующим прибавлением второго.
Рассмотрим на примере.
Если к 7 нужно прибавить сумму 15 и 23, то можно на первом этапе прибавить 23, а после, получив 30, прибавить к нему 15. Запишем пот действиям:
7+(15+23)=(7+23)+15=30+15=45
Источник: prezentacii.org
В математических примерах на сложение одним из слагаемых может быть 0. В таком случае сумма будет равна первому слагаемому. Другими словами, ноль не увеличивает число при сложении с ним.
Определенные законы существуют и для вычитания. Основные из них следующие:
- Если уменьшаемое и вычитаемое представлены одинаковыми числами, то их разность будет равна нулю. Наглядно это становится понятным на координатном луче. Отступив от начала координат 7 единиц, а потом, вернувшись на эти семь делений назад, получаем ноль.
- Аналогично третьему свойству сложения в примере на вычитание в качество вычитаемого может присутствовать ноль. Так, если от 9 нужно вычесть ноль, разность будет равна уменьшаемому, т.е. 9.
- Данное свойство также аналогично одному из свойств сложения. Если в задании требуется из числа вычесть сумму чисел, то можно выбрать и одно из них вычесть первым. Например, 16-(6+3)=(16-6)+3=10+3=13. Решение таким способом гораздо легче.
- Выбирать первостепенное действие можно и при вычитании числа из суммы. Например, (16+25)-6=(16-6)+25=10+25=35. Такое перемещение членов математического действия гораздо облегчает задачу и сокращает время на ее решение.
Приведенные свойства можно выразить в виде формул:
| Сложение | Вычитание |
| a+b=b+a | a-0=a |
| a+(b+c)=(a+b)+c | a-a=0 |
| a+0=a | a-(b+c)=(a-b)+c |
| (a+b)+c=(a+c)+b | (a+b)-c=(a-c)+b |
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так