Как сложить два комплексных числа

Что такое сложение комплексных чисел

При решении математических примеров используют разные числовые значения. Помимо натуральных, рациональных, вещественных численных множеств выделяют комплексные числа. С целью их условного обозначения используют символ \(\mathbb{C}\). Применительно к данной категории обращаются к разным свойствам, что позволяет упростить сложные вычисления и поиск ответов к задачам, в том числе, на определение суммы.

Когда b принимает нулевое значение, комплексная числовая запись приобретает формат вещественного числа. Исходя из этого утверждения, справедливо заключить, что действительные числа представляют собой частный случай комплексных. Данный вывод допустимо сформулировать с помощью подмножества:

\(\mathbb{R} \subset \mathbb{C}\)

В информационных источниках нередко встречают следующие обозначения компонентов комплексных чисел:

• Im(z) = b;
• Re(z) = a.

Предусмотрено несколько форматов представления комплексных чисел:

• алгебраическая форма: \(z = a+ib\);
• показательная запись: \(z = |z|e^{i\varphi}\);
• тригонометрический вид: \(z = |z|\cdot(\cos(\varphi)+i\sin(\varphi))\).

Перечисленные схемы записи применяют в решении тех или иных алгебраических задач. На особенность представления числовой записи обращают внимание, в том числе, при вычислении суммы.

Проанализировав сформулированное соотношение, можно сделать вывод о том, что при сложении пары комплексных чисел суммируют их действительные и мнимые компоненты. В результате смысл приобретает следующее уравнение:

\(\left(a+bi\right)+\left(c+di\right)=\left(a+c\right)+\left(b+d\right)i.\)

Свойства суммы, применимые к разным комплексным числовым записям u, v, w без ограничений:

• перестановка слагаемых: u+v=v+u;
• сочетательное качество: \(u+\left(v+w\right)=\left(u+v\right)+w\);
• особенность нулевого слагаемого: u+0=u;
• специфика противоположного компонента: \(u+\left(-u\right)=0\) ;
• представление разности с помощью операции сложения: \(u-v=u+\left(-v\right)\).

Сложение в показательной форме

При рассмотрении особенностей суммирования комплексных чисел важно отметить применение алгебраической формы записи для вычисления суммы. Другие форматы представления численных значений используют для деления, умножения и прочих операций. В этом случае полезно обратиться к показательному виду комплексных чисел. Предположим, что имеется некоторое комплексное число:

z=a+b i

Исходя из его определения, справедливо следующее соотношение:

\(e^{z}=e^{a+b i}=e^{a} e^{b i}=e^{a}(\cos b+i \sin b)\)

Когда z входит в состав множества действительных чисел, то есть \(z=a=a+0 \cdot i\), смысл приобретает такое выражение:

\(e^{z}=e^{a+0 \cdot i}=e^{a}(\cos 0+i \sin 0)=e^{a}\).

При условии, что z является мнимым, то есть \(z=b i=0+b i\), допустимо сформулировать следующее равенство:

\(e^{z}=e^{0+b i}=e^{b i}=\cos b+i \sin b.\)

В результате выполненных преобразований получим уравнение:

\(e^{b i}=\cos b+i \sin b\)

Записанное выражение носит название формулы Эйлера.

Сложение в тригонометрической форме

Представим, что задано произвольное комплексное число:

z=a+b i

На графике комплексной плоскости допустимо отметить по оси абсцисс действительный компонент числовой записи а. Одновременно с этим мнимую часть b изображают на оси ординат. На следующем шаге комплексное число несложно записать с помощью модуля. Сформулируем соответствующее выражение:

\(|z|=\sqrt{a^{2}+b^{2}}\)

Затем воспользуемся аргументом \( \phi\) для дальнейшего преобразования исходного соотношения:

\(a=|z| \cos \phi\)

\(b=|z| \sin \phi\)

Заметим, что \(\phi и |z|\) подходят по смыслу для следующих уравнений:

\(\sin \phi=\frac{y}{\sqrt{x^{2}+y^{2}}}\)

\(\cos \phi=\frac{x}{\sqrt{x^{2}+y^{2}}}, \phi \in[0 ; 2 \pi)\)

В результате получим такие равенства:

\(a=|z| \cos \phi, b=|z| \sin \phi\)

\(z=a+b i=|z| \cos \phi+i \cdot|z| \sin \phi=|z|(\cos \phi+i \sin \phi)\)

Согласно логичным рассуждениям для любого комплексного числового значения \(z=a+b i\) допустимо составить верное уравнение:

\(z=|z|(\cos \phi+i \sin \phi)\)

Записанное выражение представляет собой тригонометрический формат записи комплексного числа z.

Сложение в алгебраической форме

Суммировать комплексные числа удобно, когда они представлены в алгебраической форме. В процессе вычисления суммы таких слагаемых соответственно складывают действительные компоненты и находят результат от сложения коэффициентов, записанных в мнимых частях. Представить озвученные действия удобно в математическом виде. Предположим, что имеется пара комплексных чисел:

\({z_1} = a + bi\)

\({z_2} = c + di\)

Сумму таких комплексных числовых значений удобно записать с помощью следующего уравнения:

\({z_1} + {{\rm{z}}_2} = (a + bi) + (c + di) = (a + c) + (b + d)i\)

Допустимо в процессе решения задач и выполнения алгебраических преобразований применять к суммированию комплексных чисел стандартные подходы для работы с многочленами. В таких выражениях раскрывают скобки и приводят подобные слагаемые при необходимости. В качестве примера можно рассмотреть последовательность действий:

\(( - 19 + 7i) + (3 - 2i) = - 19 + 7i + 3 - 2i = -16 + 5i.\)

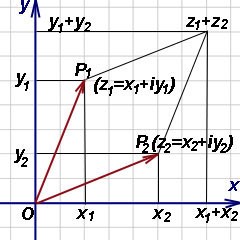
Графическое сложение комплексных чисел

Метод решения задач с помощью графиков достаточно распространен и позволяет значительно сократить объемы вычислений. Подобный способ расчетов подходит для сложения комплексных чисел. Предположим, что комплексное число \(z = (z_1; z_2)\) изображено на плоскости в виде вектора, исходная точка которого совпадает с началом координат, а конечная — соответствует \((z_1; z_2)\). Вычисление суммы комплексных числовых значений сведено к применению методу суммирования по правилу параллелограмма.

Представим, что имеется пара комплексных чисел а и b. Тогда сумму допустимо записать следующим образом:

\((а_1; а_2) + (b_1; b_2) = (а_1 + b_1; а_2+ b_2)\)

Источник: function-x.ru

Примеры решения задач

Решение

Заметим, что в условии задания записаны комплексные числа в алгебраической форме. Это условие значительно упрощает выполнение расчетов. Достаточно воспользоваться основной формулой для суммирования слагаемых и записать окончательный ответ:

\(z_{1}+z_{2}=5-6 i+(-3+2 i)=(5+(-3))+(-6+2) i=2-4 i\)

Ответ: \(z_{1}+z_{2}=2-4 i.\)

Решение:

В примере речь идет о комплексных числовых записях, представленных в алгебраическом формате. В этом случае целесообразно воспользоваться основным свойством сложения, то есть по отдельности суммировать действительные фрагменты чисел и найти сумму коэффициентов, записанных в мнимых частях выражения. Выполним необходимые математические преобразования и представим итоговый результат для каждой пары чисел.

\((4 + 5i) + (12 - 7i) = (4 + 12) + (5 - 7)i = 16 - 2i\)

\({\rm}2)( - 3 - 2i) ( - 3 - 2i) + (15 + 6i) = ( - 3 + 15) + ( - 2 + 6)i = 12 + 4i\)

\((7 + 8i) + (11 - 8i) = (7 + 11) + (8 - 8)i = 18\)

\(( - 9 - i) + (5 + i) = ( - 9 + 5) + ( - 1 + 1)i = - 4\)

\(23 + ( - 2 + 4i) = (23 - 2) + (0 + 4)i = 21 + 4i\)

Ответ: \((4 + 5i) + (12 - 7i) = 16 - 2i; ( - 3 - 2i) + (15 + 6i) = 12 + 4i; (7 + 8i) + (11 - 8i) = 18; ( - 9 - i) + (5 + i) = -4; 23 + ( - 2 + 4i) = 21 + 4i.\)

Решение

Представленные записи соответствуют алгебраической форме комплексных чисел. При вычислении суммы таких слагаемых целесообразно воспользоваться формулой, известной из теоретического материала. Допустимо выполнять преобразования выражения в процессе суммирования, чтобы упростить расчеты. Важно при этом соблюдать правила расстановки знаков перед мнимым компонентом второго слагаемого. Проведем соответствующие вычисления и запишем окончательный ответ:

\((2+5i) + (1-7i) = (2 + 1) + (5 – 7)i = 3 – 2i\)

Ответ: \((2+5i) + (1-7i) = 3 – 2i.\)

Решение

Показательная форма комплексного числового значения предполагает первоначальное определение модуля и аргумента. С этой целью необходимо произвести некоторые преобразования. Выполним нужные действия:

\(|z|=\sqrt{3^{2}+(-4)^{2}}=\sqrt{9+16}=\sqrt{25}=5\)

\(\phi=\operatorname{arctg} \frac{-4}{3}=-\operatorname{arctg} \frac{4}{3}\)

На следующем шаге следует воспользоваться принципом записи комплексного числа с применением рассчитанного ранее модуля и аргумента:

\(z=|z| e^{i \phi}=5 e^{-i \operatorname{arctg} \frac{4}{3}}\)

Ответ: \(z=5 e^{-i \operatorname{arctg} \frac{4}{3}}.\)

Решение

По определению из курса теории известно, что комплексное число состоит из действительной и мнимой части. Применительно к выражению из условия задания идентифицируем компоненты числовой записи. Получим, что действительный фрагмент имеет нулевое значение, а мнимая часть представлена как b=-1. На основании полученной информации допустимо вычислить модуль исходного комплексного числа:

\(|z|=\sqrt{0^{2}+(-1)^{2}}=\sqrt{0+1}=1\)

На следующем этапе решения задачи целесообразно посчитать аргумент для рассматриваемого комплексного числового значения:

\(\phi=\operatorname{arctg} \frac{-1}{0}=-\frac{\pi}{2}=\frac{3 \pi}{2}\)

С помощью записанных выше выражений несложно преобразовать начальный вариант записи в тригонометрическую форму:

\(z=1 \cdot\left(\cos \frac{3 \pi}{2}+i \sin \frac{3 \pi}{2}\right)=\cos \frac{3 \pi}{2}+i \sin \frac{3 \pi}{2}\)

Ответ: \(z=\cos \frac{3 \pi}{2}+i \sin \frac{3 \pi}{2}\).