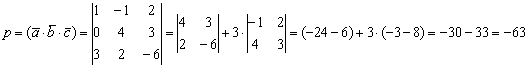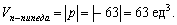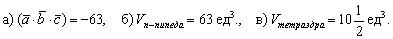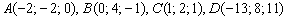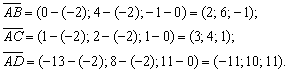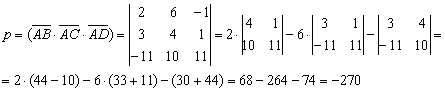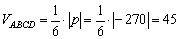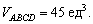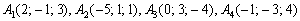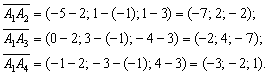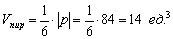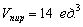Смешанное произведение векторов

Что такое смешанное произведение векторов 

При сравнении данной алгебраической операции со скалярным произведением можно заметить, что действия выполняются с двумя векторами. Для примера их можно обозначить в виде \(\vec{a}\) и \(\vec{b}\)

В качестве обозначения действия используют следующее выражение:

\(\left[ \vec{a}\times \vec{b}\right]\)

В качестве доказательства результат векторного произведения можно записать, таким образом:

\(\left[ \vec{a}\times \vec{b}\right]=\vec{N}\)

Векторное произведение \(\left[ \vec{a}\times \vec{b}\right]\) неколлинеарных векторов \(\vec{a}\) и \(\vec{b}\) рассматриваемых в определенном порядке, является вектором \(\vec{N}\). Длина данного вектора в численном выражении представляет собой площадь параллелограмма, который построен на данных векторах.

Произвольный вектор \(\vec{N}\) ортогонален векторам \(\vec{a}\) и \(\vec{b}\). Данный вектор направлен таким образом, что базис \(\vec{a}; \ \vec{b}; \vec{N}\) характеризуется правой ориентацией:

Обозначить действие можно следующим образом:

\(\left( \vec{a}\times \vec{b}\times \vec{c}\right)\)

В качестве смешанного произведения \(\left( \vec{a}\times \vec{b}\times \vec{c}\right)\) некомпланарных векторов \(\vec{a}, \ \vec{b}, \ \vec{c}\), которые рассматривают в определенном порядке, можно представить объем геометрической фигуры параллелепипеда.

Многоугольник построен на основании данных векторов. Знак «+» добавляют к значению в том случае, когда базис \(\left( \vec{a}\times \vec{b}\times \vec{c}\right)\) правый, и знаком «-», когда базис \(\left( \vec{a}\times \vec{b}\times \vec{c}\right)\) левый.

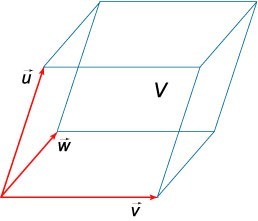
Геометрический смысл смешанного произведения векторов заключается в том, что объем параллелепипеда, который построен с помощью трех векторов \(\mathbf{u}, \mathbf{v}, \mathbf{w}\) представляет собой модуль смешанного произведения этих векторов:

\(V = \left| {\left( {\mathbf{u},\mathbf{v},\mathbf{w}} \right)} \right| = \left| {\mathbf{u} \cdot \left( {\mathbf{v} \times \mathbf{w}} \right)} \right|\)

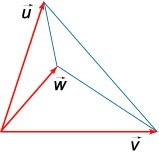
Пирамида, которая построена на трех векторах \(\mathbf{u}, \mathbf{v}, \mathbf{w}\) обладает объемом, равным:

\(V = \large\frac{1}{6}\normalsize \left| {\left( {\mathbf{u},\mathbf{v},\mathbf{w}} \right)} \right| = \large\frac{1}{6}\normalsize \left| {\mathbf{u} \cdot \left( {\mathbf{v} \times \mathbf{w}} \right)} \right|\)

Формула вычисления смешанного произведения трех векторов

В качестве формулы для нахождения смешанного произведения трех векторов \(\mathbf{u}, \mathbf{v} \ и \ \mathbf{w}\) используют скалярное произведение вектора \(\mathbf{u}\) на векторное произведение векторов \(\mathbf{v} \ и \ \mathbf{w}\)

Выражение можно записать следующим образом:

\(\left( {\mathbf{u},\mathbf{v},\mathbf{w}} \right) = \mathbf{u} \cdot \left( {\mathbf{v} \times \mathbf{w}} \right) = \mathbf{v} \cdot \left( {\mathbf{w} \times \mathbf{u}} \right) = \mathbf{w} \cdot \left( {\mathbf{u} \times \mathbf{v}} \right)\)

Свойства, особенности умножения в системе координат

При выполнении действий со смешанным произведением векторов целесообразно использовать справедливые закономерности. Их применение упрощает решение задач. К таким свойствам относят:

1. Перестановка компонентов произведения:

\(\left( {\mathbf{u},\mathbf{v},\mathbf{w}} \right) = \left( {\mathbf{w},\mathbf{u},\mathbf{v}} \right) = \left( {\mathbf{v},\mathbf{w},\mathbf{u}} \right) = -\left( {\mathbf{v},\mathbf{u},\mathbf{w}} \right) = -\left( {\mathbf{w},\mathbf{v},\mathbf{u}} \right) = -\left( {\mathbf{u},\mathbf{w},\mathbf{v}} \right)\)

2. Умножение на какое-то определенное число:

\(k\mathbf{u} \cdot \left( {\mathbf{v} \times \mathbf{w}} \right) = k\left( {\mathbf{u},\mathbf{v},\mathbf{w}} \right)\)

При рассмотрении смешанного произведения в системе координат можно записать следующее выражение:

\(\left( {\mathbf{u},\mathbf{v},\mathbf{w}} \right) = \mathbf{u} \cdot \left( {\mathbf{v} \times \mathbf{w}} \right) = \left| {\begin{array}{*{20}{c}} {{X_1}} & {{Y_1}} & {{Z_1}}\\ {{X_2}} & {{Y_2}} & {{Z_2}}\\ {{X_3}} & {{Y_3}} & {{Z_3}} \end{array}} \right|\)

В данном случае: \( \mathbf{u} = \left( {{X_1},{Y_1},{Z_1}} \right), \mathbf{v} = \left( {{X_2},{Y_2},{Z_2}} \right), \mathbf{w} = \left( {{X_3},{Y_3},{Z_3}} \right)\)

В таком случае, один из указанных векторов можно определить с помощью двух других векторов:

\(\mathbf{w} = \lambda \mathbf{u} + \mu \mathbf{v}\)

В данной форме выражении \lambda, \mu являются некоторыми действительными числами.

Двойное векторное произведение трех векторов \( \mathbf{u}, \mathbf{v} \ и \ \mathbf{w}\) представляет собой векторное произведение в виде формулы:

\(\mathbf{u} \times \left( {\mathbf{v} \times \mathbf{w}} \right) = \left( {\mathbf{u} \cdot \mathbf{w}} \right)\mathbf{v} - \left( {\mathbf{u} \cdot \mathbf{v}} \right)\mathbf{w} = \left| {\begin{array}{*{20}{c}} \mathbf{v} & \mathbf{w}\\ {\left( {\mathbf{u} \cdot \mathbf{v}} \right)} & {\left( {\mathbf{u} \cdot \mathbf{w}} \right)} \end{array}} \right| \)

Разбор типовых задач, примеры решения

Требуется определить: значение смешанного произведения векторов, объемы параллелепипеда и тетраэдра, которые построены на основе заданных векторов.

Решение:

Необходимо воспользоваться формулой смешанного произведения

 

В данном случае определитель раскрывают, ориентируясь на первую колонку.

Объем параллелепипеда, который построен на рассматриваемых в условии задачи векторах, можно найти с помощью модулю смешанного произведения этих векторов:

 

В случае определения объема тетраэдра следует использовать выражение:

 

Ответ:  

 

Решение:

В первую очередь необходимо найти векторы:

 

Определить смешанное произведение векторов можно, таким образом:

 

В данном случае определитель матрицы будет раскрыт по первой строке.

Объем треугольной пирамиды можно рассчитать:

 

Ответ: 

Необходимо определить объем этой геометрической фигуры.

Решение:

В первую очередь следует определить векторы:

 

В этом случае раскрытие определителя осуществляется по первой строке.

Объем пирамиды будет записан с помощью равенства:

 

Ответ: