Смежные углы
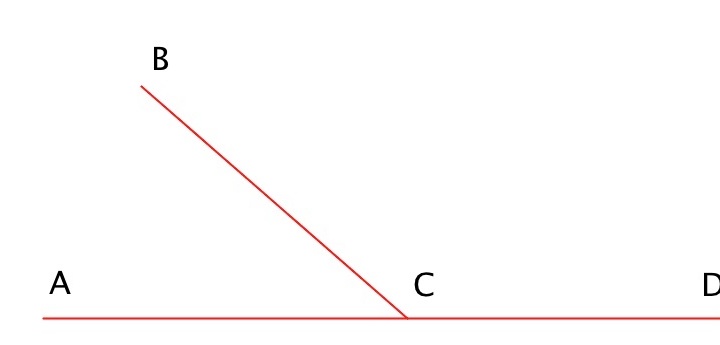
Смежные углы — это два угла, у которых есть общая вершина и одна сторона, а две другие стороны являются продолжением друг друга и лежат на одной прямой.
Свойства и виды смежных углов в геометрии
- Так как две стороны смежных углов образуют прямую линию, то вместе они составляют развернутый угол. Его градусная мера составляет 180^\circ. Следовательно — сумма смежных углов тоже равна \(180^\circ.\)
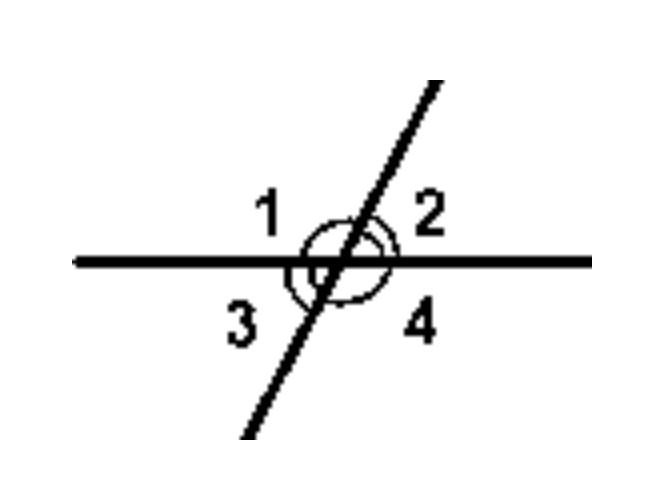
- Если две прямые пересекаются, то они образуют две пары смежных углов: \(\angle1\) и \(\angle2\), \(\angle3\) и \(\angle4\), а также \(\angle1\) и \(\angle3\), \( \angle2\) и \(\angle4\). При этом объединение пар, которые обозначены обозначениями 1 и 4, 2 и 3, представляют из себя вертикальные углы, а значит — они равны. Поэтому рассматривать можно только одну из пар смежных углов, другая окажется идентична по всем показателям.
![Виды смежных углов Виды смежных углов]()
- У смежных углов одинаковые синусы.
- Для косинусов и тангенсов тоже распространяется равенство, но их значения противоположны по знаку.
- Чтобы построить смежный угол уже заданному, требуется продлить одну из сторон существующего угла дальше вершины.
В паре, если один угол тупой, то по правилу другой обязательно острый.
Если один из углов является прямым, то второй тоже прямой.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Как найти, чему равна сумма
Сумма смежных углов всегда составляет 180 градусов.
Отсюда следует формула:
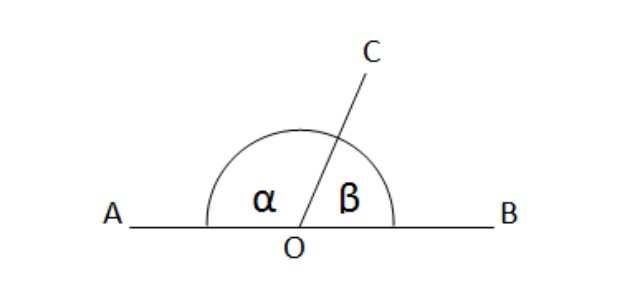
\(\angle\alpha+\angle\beta=180^\circ\)
\(\angle\alpha=180^\circ-\angle\beta\)
\(\angle\beta=180^\circ-\angle\alpha\)
Примеры решения задач
Задача №1
Дано: \(\angle\alpha\) и \(\angle\beta\) — смежные, \(\angle\beta=60^\circ\).
Найти: чему равен \(\angle\alpha\).
Решение
Так как углы смежные, значит:
\(\angle\alpha+\angle\beta=180^\circ.\)
\(\angle\alpha=180^\circ-\angle\beta.\)
\(\angle\alpha=180^\circ-60^\circ=120^\circ.\)
Ответ: \(\;\angle\alpha=120^\circ\).
Задача №2
Дано: \( \angle\alpha\) и \(\angle\beta\) — смежные, \(\angle\alpha\) на \(30^\circ\) больше, чем \(\angle\beta.\)
Найти: чему равны \(\angle\alpha\) и \(\angle\beta.\)
Решение
Допустим,\( \angle\beta=x\), тогда \(\angle\alpha=x+30^\circ.\)
Так как сумма смежных углов равна 180 градусов, то получаем уравнение, которое выглядит, как:
\(x+x+30^\circ=180^\circ\)
\(2x=180^\circ-30^\circ\)
\(2x=150^\circ\)
\(x=75^\circ\)
Значит, величина \(\angle\beta=75^\circ.\)
Чтобы найти \(\angle\alpha\), нужно выполнить стандартные вычисления согласно теореме о сумме:
\(\angle\alpha=180^\circ-\angle\beta=180^\circ-75^\circ=105^\circ.\)
Ответ: \(\angle\alpha=105^\circ.\)
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так