Какие углы называются смежными, а какие вертикальными
Смежные и вертикальные углы – определение
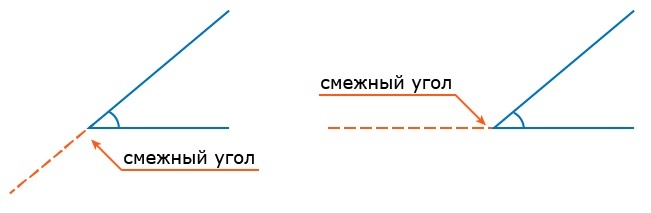
Смежные углы – это два угла, у которых одна сторона общая, а две другие стороны являются дополняющими лучами.
Вертикальные углы – это два угла, стороны одного из которых являются дополняющими лучами сторон другого.
Теорема о смежных и вертикальных углах
Теорема о СУ гласит, что их сумма равна 180°.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Доказательство данного положения легко узнать на практике при помощи построения. Так как у СУ есть общая сторона, это значит, что они расположены на развернутом угле. А поскольку такая геометрическая фигура равна 180°, то и сумма СУ будет приравниваться к этому же значению.
Следствием из данной теории будет то, что если смежные углы равны, то они прямые. ПУ = 90°. Это есть половина от величины развернутого угла, на котором и находятся два СУ.
Еще одно следствие. Если два угла равны, то смежные с ними тоже имеют одно значение.
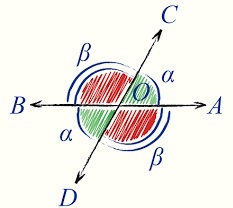
Теорема о вертикальных углах гласит, что ВУ равны. Доказательство: Рассмотрим ВУ AOB и COD. ∠BOD смежный для каждого из ∠AOB и ∠COD. По теореме 1 ∠АОВ+∠BOD=180°, ∠COD+∠BOD=180°. Из этого ∠АОВ=∠COD.
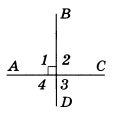
Следствие 1. Угол, смежный с прямым, есть прямой угол. Рассмотрим две пересекающиеся прямые АС и BD. Они образуют четыре угла. Если один из них прямой, то остальные также прямые (1 и 2, 1 и 4 — смежные, 1 и 3 — вертикальные). В этом случае говорят, что эти прямые пересекаются под прямым углом и называются перпендикулярными (или взаимно перпендикулярными). Перпендикулярность АС и BD обозначается так: AC ⊥ BD.
Смежные углы
Перечислим не отмеченные ранее свойства СУ:
- угол, смежный с прямым, является прямым; смежный с острым – тупым; смежный с тупым – острым;
- чем больше угол, тем меньше СУ, и наоборот;
- биссектрисы СУ образуют прямой угол.
Приведем пример решения задачи со СУ.
Задача
∠1 и ∠2 – смежные, ∠1 : ∠2 = 3 : 7.
Найти ∠1 и ∠2.
Решение
Пусть х – коэффициент пропорциональности. Тогда ∠1=3х, ∠2=7х. Так как ∠1+∠2=180°(по теореме о СУ), то 3х+7х=180°, 10х=180°, х=18°. Следовательно ∠1=3×18°=54°, ∠2=7×18°=126°
Ответ: ∠1=54°, ∠2= 126°.
Вертикальные углы
Отметим также неупомянутые свойства ВУ:
- ВУ по-другому называют углом между двумя прямыми;
- биссектрисы ВУ лежат на одной прямой.
Приведем пример решения задачи с ВУ.
Задача
Пусть на рисунке 1 ∠COD равен 45°. Чему равны ∠AOB и ∠AOC ?
Решение
Так как ∠COD и ∠AOB вертикальные, то значит, они равны, а тогда:
\(\angle AOB=\angle COD=45^\circ\)
\(∠AOB\angle AOB+\angle AOC=180^\circ\)
Из этого \(\angle AOC=180^\circ-\angle AOB=180^\circ-45^\circ=135^\circ.\)
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так