Какое соотношение между сторонами и углами треугольника
Теорема и доказательство с формулами
В процессе изучения науки геометрии приходится часто иметь дело с разнообразными геометрическими фигурами. Одной из таких форм является треугольник. На вычисление параметров разных элементов геометрического объекта предусмотрено множество задач. Многие из подобных примеров обладают повышенной сложностью, но вполне разрешимы, если знать закономерности, описывающие связи компонентов треугольника.
Наиболее востребованным знанием является соотношение, демонстрирующее взаимосвязь между величинами углов и сторон в треугольнике. Эти положения несложно сформулировать, руководствуясь логикой. В процессе необходимо проанализировать плоский треугольный объект, состоящий из трех отрезков. Расположение рассматриваемых отрезков такое, что начальная точка одного из них обязательно совпадает с конечной точкой следующего.
В результате полученные стороны треугольника обладают точками пересечения, называемыми вершинами. Угол, который соответствует каждой из таких вершин, является внутренним. Независимо от типа и размеров подобного геометрического объекта, он обладает тремя вершинами и аналогичным количеством сторон. В качестве обозначения треугольника используют заглавные буквы латинского алфавита, а когда требуется записать длины сторон, целесообразно воспользоваться строчными буквами.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Изучая треугольник, несложно заметить простоту его построения. Однако при дальнейшем рассмотрении можно выявить довольно сложные закономерности, объединяющие параметры этой геометрической фигуры. Простой, на первый взгляд, многоугольник имеет множество характерных свойств, смысл которых позволяет формулировать и доказывать полезные в практическом смысле теоремы и следствия из них.
Теорема: в геометрической фигуре, которая является треугольником, напротив большей стороны расположен угол с наибольшей градусной мерой.
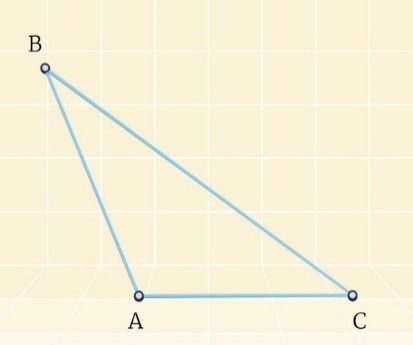
Представим, что имеется некоторый треугольник \(\Delta ABC\). Предположим, что в этом геометрическом объекте стороны соотносятся между собой таким образом:
AB > AC
Согласно записанной ранее теореме, необходимо представить доказательства следующего положения:
\(\angle С > \angle B\)
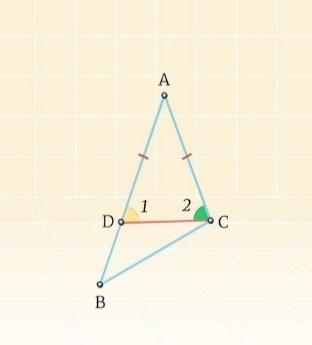
Начнем доказательство с построения наглядного изображения:
Источник: resh.edu.ru
Далее построим на стороне АВ отрезок, который по величине соответствует АС. Получим следующий рисунок:
Источник: resh.edu.ru
Заметим, что AD < AB. Исходя из этого, можно определить положение точки D, которое соответствует отрезку между А и В. Таким образом, угол 1 представляет собой составной компонент угла С, то есть:
\(\angle С > \angle 1\)
С другой стороны, угол 2 является внешним углом для геометрического треугольного объекта ВDС. Исходя из этого и руководствуясь свойством внешнего угла треугольника, можно заключить следующее:
\(\angle 2 > \angle B\)
Первый и второй углы расположены при основании треугольника АDC, который является равнобедренным. В результате:
\(\angle 2 = \angle 1\)
По доказательству осталось сделать итоговый вывод:
\(\angle С > \angle 1\)
\(\angle 2 = \angle 1\)
\(\angle 2 > \angle B\)
Таким образом:
\(\angle С > \angle B\), что доказывает сформулированную в начале теорему.
Обратная теорема: напротив самого большого угла в геометрической треугольной фигуре расположена сторона с максимальной длиной.
Предположим, что имеется \(\Delta ABC\), в котором углы соотносятся друг с другом таким образом, что:
\(\angle С > \angle В\)
Необходимо представить доказательства справедливости следующего соотношения:
АВ > AC
В процессе доказательства выдвинем следующие взаимоисключающие предположения:
АВ = АС
АВ < АС
В первой ситуации получается треугольник с парой равных друг другу сторон, то есть равнобедренный. В таком случае, руководствуясь ключевой закономерностью этой геометрической фигуры, запишем следующее справедливое равенство, вытекающее из вышесказанного:
\(\angle С = \angle В\)
Заметим, что сформулированный вывод противоречит условию задания. Следовательно, утверждение о равенстве сторон АВ и АС является ошибочным.
В том случае, когда сторона АВ меньше по сравнению со стороной АС, целесообразно прийти к выводу о следующем соотношении:
\(\angle В > \angle С\)
Это соотношение подтверждено доказанной ранее теоремой. Однако подобное положение вновь противоречит условию задачи. Тогда второе предположение также является недействительным. Обратную теорему можно считать доказанной.
Первое следствие: в прямоугольном треугольнике величина гипотенузы превышает аналогичные параметры катета.
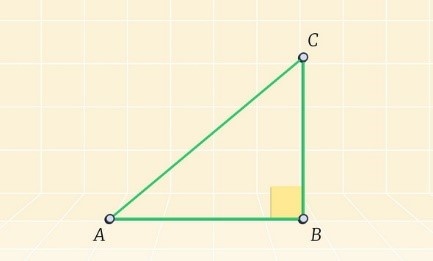
В процессе доказательств изобразим произвольный треугольник АВС. Пусть один из углов этого многоугольника будет прямым, то есть:
\(\angle В = 90°\)
Сформулируем соотношение, которое требуется доказать:
АС > СВ
Источник: resh.edu.ru
Заметим, что:
\(\angle В > \angle А\)
Это объясняется тем, что угол В является прямым по условию задачи. Ранее была записана обратная теорема, согласно которой угол А является острым и верно следующее соотношение:
АС > СВ
Первое следствие доказано. Можно переходить к рассмотрению второго следствия.
Второе следствие, то есть признак равнобедренного треугольника: в случае равенства пары углов в геометрической треугольной фигуре этот треугольник является равнобедренным.
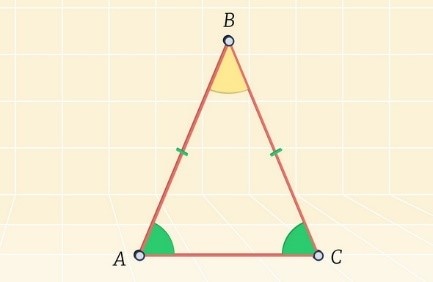
На рисунке представлен \(\Delta ABC\). Предположим, что два угла в этой геометрической фигуре обладают одинаковыми градусными мерами, то есть:
\(\angle А = \angle С\)
Требуется доказать тот факт, что рассматриваемый треугольник является равнобедренным. Начать процесс обоснования теоремы следует с изображения геометрического объекта, описанного в условиях задания.
Источник: resh.edu.ru
В процессе аргументации теории нужно прийти к выводу о том, что:
АВ = ВС
Представим, что сторона АВ больше по величине стороны ВС. Из этого легко сделать вывод о справедливости следующего соотношения:
\( \angle С > \angle А\)
Это верно, так как работает теорема, доказанная ранее о том, что напротив большей стороны расположен больший угол. Однако соотношение противоречит условию задания, где предполагается равенство этих углов. В таком случае стороны АВ и ВС равны, а рассматриваемый треугольник является равнобедренным, что и требовалось доказать.
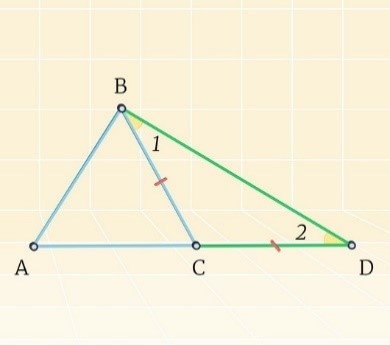
Теорема: любая из сторон треугольной геометрической фигуры меньше по сравнению с суммарной величиной пары других сторон.
Представим, что имеется некоторый треугольник \(\Delta ABC\). В рассматриваемом треугольнике стороны должны соотноситься следующим образом:
АВ < АС + СВ
Наглядное изображение геометрической фигуры представлено на рисунке ниже:
Источник: resh.edu.ru
В процессе обоснования выдвинутой теоремы необходимо построить продолжение для стороны АС, на котором можно отмерить отрезок СD, равный по величине стороне ВС. Заметим, что \(\Delta BCD\) является равнобедренным. К такому выводу несложно прийти, исходя из определения равнобедренного треугольного объекта с точки зрения геометрии. Таким образом:
\( \angle 1 = \angle 2\)
В полученном треугольнике ABD углы соотносятся между собой следующим образом:
\(\angle ABD > \angle 1\)
Это верно, так как угол 1 входит в состав \(\angle ABD\). Исходя из данного соотношения, запишем:
\(\angle ABD > \angle 2\)
Последнее положение справедливо по равенству первого и второго угла. В связи с тем, что напротив большего угла расположена максимальная по величине сторона, целесообразно сформулировать такой вывод:
AB < AD
AD = AC + CD
Известно, что сторона CD не отличается по величине от ВС. Исходя из этого положения, запишем:
AD = AC + CВ
AB < AC + СВ
Теорема доказана. Исходя из сформулированного соотношения, можно вывести следствие. Рассмотрим его подробнее.
Следствие: для каких-либо трех точек А, В, С, которые не расположены на одинаковой прямой, характерны такие неравенства:
AB < AC + CB
AC < AB + BC
BC < BA + AC.
Представим наглядное изображение треугольного геометрического объекта, в состав которого входят стороны, перечисленные в тексте следствия для теоремы.
Источник: resh.edu.ru
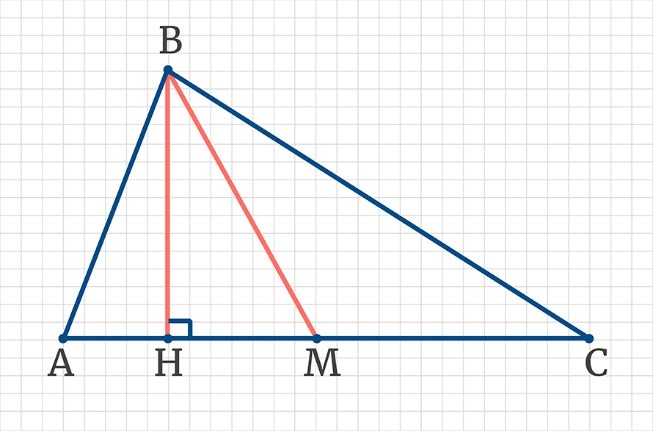
Доказать озвученное утверждение можно с помощью теоремы о взаимосвязи углов и сторон треугольника. В процессе важно подтвердить справедливость соотношения между элементами геометрической фигуры, согласно которому при построении медианы и высоты из одинаковой вершины данная медиана не меньше высоты, проведенной из той же вершины. Потребуется изобразить еще один рисунок для наглядности доказательства:
Источник: resh.edu.ru
В треугольнике АВС отрезок ВМ представляет собой медиану, а отрезок ВН играет роль высоты. Необходимо представить доказательства справедливости следующего соотношения:
\(ВМ \geq ВН\)
Доказать утверждение целесообразно с помощью обратной формулировки положения. Таким образом, следует предположить, что:
\(АВ \neq ВС\)
Тогда ВМ и ВН не совпадают, исходя из того, что по свойству равнобедренного треугольника высота и медиана совпадают, когда построены к его основанию. Далее проанализируем треугольник ВНМ. Данная фигура имеет прямой угол Н, то есть является прямоугольным треугольником. В таком случае угол Н с максимальной градусной мерой позволяет сделать следующий вывод:
ВМ > ВН
Это неравенство верно по обратной теореме о соотношениях между сторонами и углами треугольника. Затем можно приступать к анализу второго случая, когда АВ = ВС. Тогда треугольник АВС является равнобедренным, согласно его определению. В таком случае отрезки ВМ и ВН имеют одинаковые длины по свойству высоты и медианы в равнобедренном треугольнике. Следствие из теоремы доказано, так как:
\(ВМ \geq ВН.\)
Задачи
Имеется треугольный геометрический объект АВС. Данная фигура является равнобедренной со сторонами, которые равны 8 см и 4 см. Необходимо определить длину третьей стороны.
Решение
Исходя из определения для равнобедренного треугольника, пара его боковых сторон равны по длине. Таким образом, это будет сторона, которая составляет 4 см или 8см. Заметим, что вариант со стороной 4см не подходит в данном случае, так как:
8см = 4 см + 4 см
Это положение противоречит теореме о соотношениях между сторонами треугольника: каждая сторона треугольника меньше суммы двух других сторон. По этой причине целесообразно предположить соответствие боковых сторон 8 см. Тогда, по теореме о соотношениях между сторонами треугольника, каждая сторона треугольника меньше суммы двух других сторон. В результате можно сформулировать следующий вывод:
4 см < 8 см + 8 см
8 см < 8 см + 4 см
Из справедливости записанного соотношения можно заключить соответствие длины третьей стороны величине в 8 см.
Ответ: 8 см.
Треугольник АВК является равнобедренным с основанием ВК. Периметр этой геометрической фигуры равен 29 см, а разность пары сторон составляет 5 см. Какой-то из внешних углов треугольника является острым. Требуется вычислить величины боковой стороны АВ и основания ВК.
Решение
Исходя из информации по заданию, какой-то из внешних углов имеет градусную меру меньше, чем 90 градусов. В таком случае один из внутренних углов будет тупым, а это может быть, в равнобедренном треугольнике, только вершина над основанием треугольника. Сформулированное положение верно по следствию из теоремы о сумме углов треугольника. На основании вышесказанного можно заключить, что основание ВК является максимальным по длине в треугольнике АВК. Это понятно из теоремы о соотношении между углами и сторонами треугольника. Получим, что:
ВК – АВ = 5 см
ВК = 5см + АВ.
Воспользуемся определением равнобедренной треугольной фигуры, которое уже знакомо из теоретического курса. Исходя из этой формулировки, можно сделать вывод о равенстве боковых сторон, то есть:
АВ = АК.
Заметим, что под периметром треугольника понимают результат сложения длин трех его сторон.
Источник: resh.edu.ru
Выполним необходимые вычисления:
\(Р \Delta АВК = АВ + АК + ВК = 29\)см (по условию)
2АВ + ВК = 29 см
2АВ +5см + АВ = 29 см
3АВ = 24 см
АВ = 8 см, ВК = 8 + 5 =13 см.
Ответ: ВК = 13 см; АВ = 8 см.
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так