Основные сведения о способах задания функции, примеры решения задач

Способы задания функций

«Задать функцию» означает установить правило (закон), с помощью которого по данным значениям независимой переменной (из числа возможных) следует находить соответствующие им значения функции.

Табличный способ

При этом способе задания функции в таблицу вносятся значения независимой переменной х и соответствующие им значения зависимой переменной у. Такой способ широко распространен: таблицы логарифмов, корней, степеней чисел.

Основное преимущество табличного способа задания функции — возможность, не проводя дополнительных измерений и вычислений, определить те или другие конкретные значения сразу, если известен аргумент. Недостатком способа является то, что таблица определяет функцию не полностью, а лишь для некоторых значений аргумента: в ней отсутствуют промежуточные значения и в целом их количество ограничено. Также таблица не дает полного представления о характере зависимости функции от изменения аргумента.

Применение табличного способа оправдано в том случае, когда область определения функции является дискретным конечным множеством. В некоторых случаях с помощью интерполяции можно приближенно вычислить значения функции, отсутствующие в таблице и соответствующие промежуточным значениям аргумента.

Графический способ

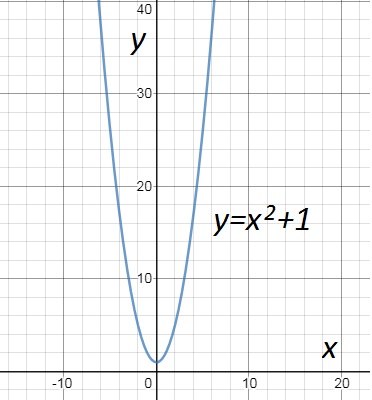
При графическом способе в системе координат строится график, множество точек которого соответствуют уравнению y=f(x), задающему функцию. Ось абсцисс задает значения аргумента, ось ординат — функции.

Главный недостаток графического способа задания функции заключается в том, что с помощью графика, даже зная численное значение аргумента, невозможно точно определить значение функции. Однако этим способом часто пользуются в физике и технике, так как благодаря своей наглядности он позволяет представить характер заданной функции в целом.

Часто графическое задание функции комбинируют с аналитическим способом, а именно с уравнением, задающим данный график. Такое сочетание позволяет представить функцию наглядно, и при этом точно рассчитать необходимые значения.

Аналитический способ

Аналитический способ состоит в том, что связь между аргументом и функцией выражается с помощью формулы, представляющей собой уравнение. В левой части уравнения находится зависимая переменная у, в правой — выражение, состоящее из независимой переменной х, постоянных, математических операций и известных элементарных функций. Такой способ задания функции очень распространен, так как дает возможность для каждого возможного значения аргумента найти соответствующее ему значение функции точно или с большой точностью.

Зависимость y от x задана явно, если уравнение имеет вид y = f(x).

Если формула выглядит как F(x,y) = 0, то функция задана неявно.

Достоинства этого способа: компактность, лаконичность, возможность вычисления значения функции при произвольном значении аргумента, возможность применения к данной функции аппарата математического анализа. Недостатком является отсутствие наглядности, которое можно компенсировать построением графика.

Интервальный способ

Функция может быть определена разными формулами на разных интервалах значения аргумента.

Параметрический способ

Для выражения функции параметрическим способом вводится дополнительная переменная t, через которую задают значения х и у.

\(\left\{\begin{array}{l}у=у(t)\\x=x(t)\end{array}\right.\)

Словесный способ

При выражении функции словесным способом, характер зависимости выражен словами.

Такой функцией обозначают наибольшее из целых чисел, которое меньше либо равно x. Если x=а+b, где а — целое число, а b ∈ [0; 1), то [x] = а. Функция E(x) = [x] постоянна на промежутке [a; a+1), и на нем [x] = a.

\(y ={x} = x - [x]\), где [x] — целая часть числа x. Если x — произвольное число, то его можно представить в виде \(x=а+b (а = [x])\), где a — целое число и b∈[0; 1), поэтому \({x}=a+b-a=b\).

Недостатками данного способа задания функции являются невозможность проведения сложных вычислений и отсутствие наглядности. Главное преимущество — возможность задать те функции, которые сложно выразить аналитически.

Пример решения задачи

 Дано: функция задана уравнением \(у=х^2+1\).

Найти: построить график функции и составить таблицу для целых значений \(х∈[0; 5]\).

Решение:

х	0	1	2	3	4	5
у	1	2	5	10	17	26

Задача