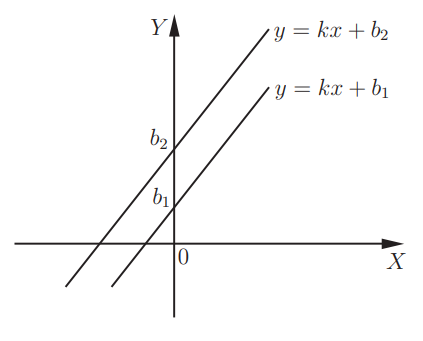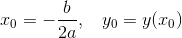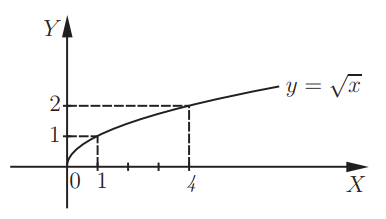Свойства степенных функций, построение графиков
Степенная функция — что это такое
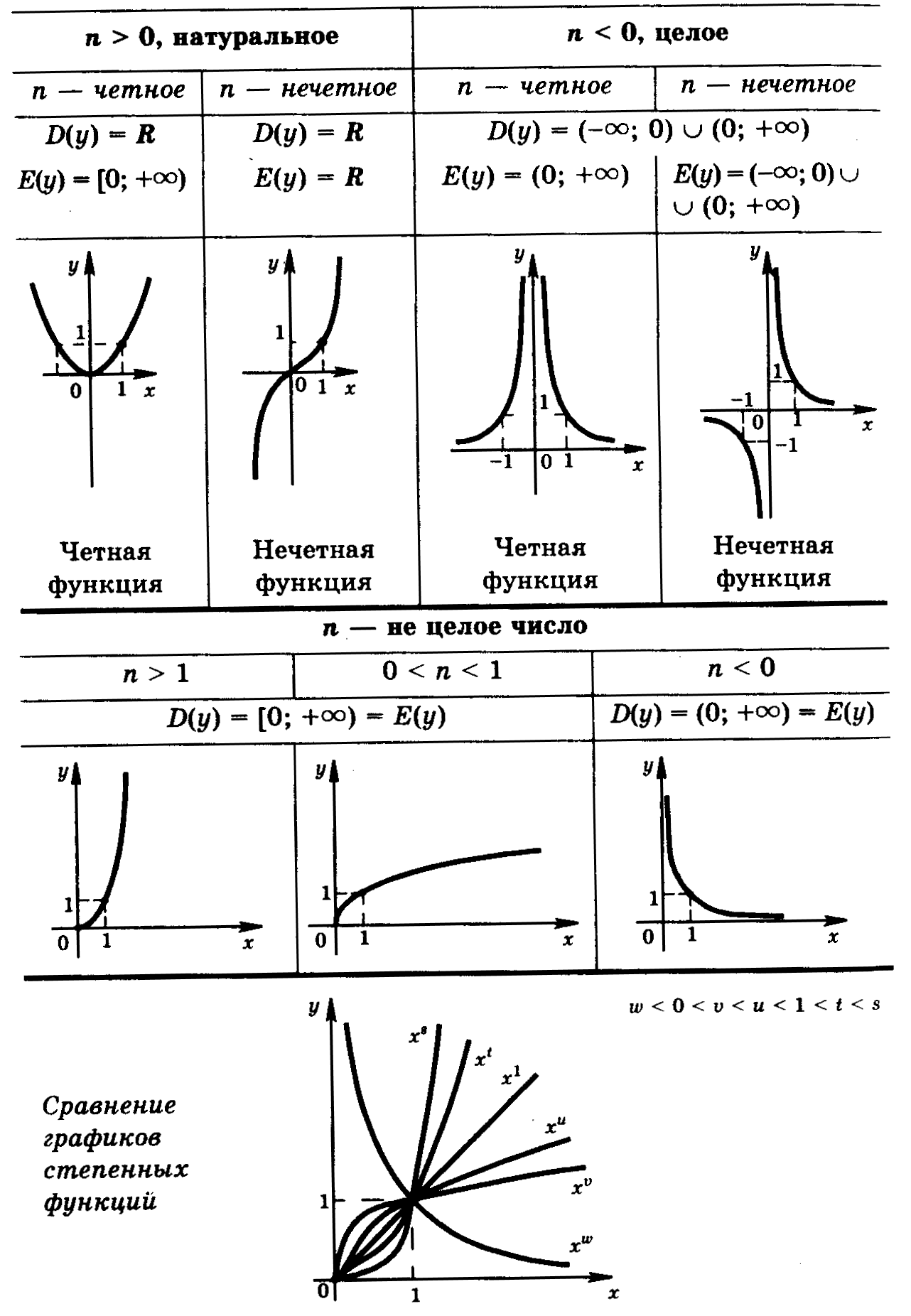
Степенная функция является функцией вида \(x^{a}\), где а – целое, дробное, положительное или отрицательное число.
К степенным функциям в теории относятся следующие виды:
- линейная функция \(y = kx + b\);
- квадратичная парабола \(y = x^{2}\) (в общем виде: \(y = ax^{2} + bx + c)\);
- кубическая парабола \(y = x^{3}\);
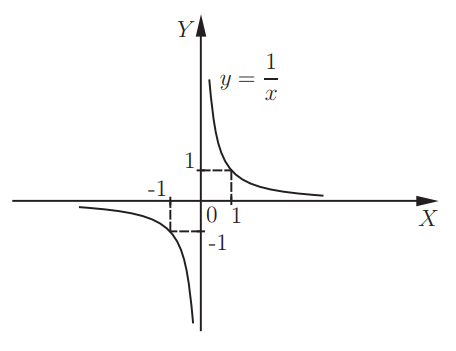
- гипербола \(y = \frac{1}{x}\), которую можно представить в виде\( y = x^{-1};\)
- функция \(y =\sqrt{x}\), так как \(\sqrt{x} = x^{\frac{1}{2}}.\)
В качестве примера можно рассмотреть описание функции: \(y=x^{\frac{m}{n}}\). В первую очередь следует проанализировать функции с показателем степени \(\frac{m}{n}>1\). Например, задана некая функция:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
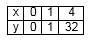
\(y=x^2*5.\)
Исходя из обозначения, при x≥0, область определения рассматриваемой функции – это луч [0;+∞).
Далее следует записать таблицу значений:
Затем можно сравнить несколько степенных функции следующим способом:
\(y=x^2;\)
\(y=x^{2,5};\)
\(y=x^3.\)
Число 2,5 находится между 2 и 3. В таком случае можно предположить, что и график рассматриваемой функции расположен между соответствующими графиками. Можно представить разные характеристики х, чтобы сравнить значения функций, которые зависят от x:
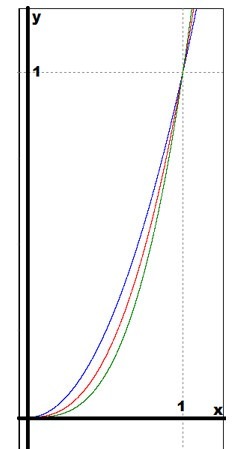
При \(0<x<1\), получается \(x^6<x^5<x^4\), но и выполняется \(\sqrt{x^6}<\sqrt{x^5}<\sqrt{x^4}\) или \(x^3<x^{2,5}<x^2.\)
При \(x>1\), получается \(x^4<x^5<x^6\), но и выполняется \(\sqrt{x^4}<\sqrt{x^5}<\sqrt{x^6}\) или \(x^2<x^{2,5}<x^3.\)
Все графики целесообразно построить на одном рисунке. В первом случае \(0<x<1\):
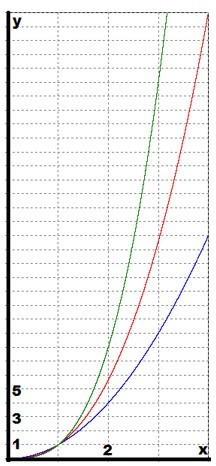
В данном случае синий цвет соответствует функции \(y=x^2\); красный:\( y=x^{2,5}\); зеленый: \(y=x^3\). На следующем этапе нужно построить графики по порядку на всей области определения функции \(y=x^{2,5}\). Цвет графиков останется прежним, как и на предыдущем рисунке:
График функции \(y=x^{\frac{m}{n}}\), \((m>n)\) является кривой, которая проходит через точки (0,0) и (1,1), и напоминает ветвь параболы. При увеличении показателя график функции в верхнем положении становится круче.
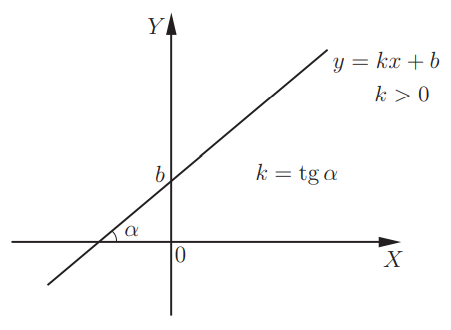
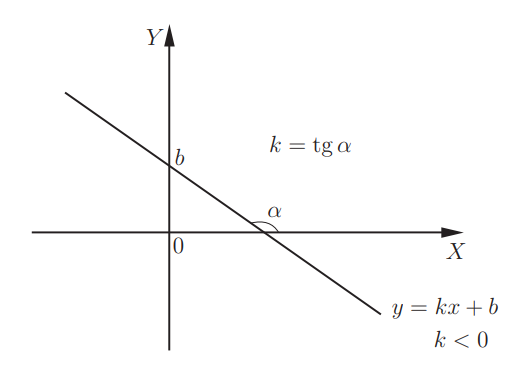
Линейная функция y = kx + b. Графиком данной функции является прямая линия. Для того, чтобы ее построить, требуется пара точек. При k > 0, линейная функция будет расти. При увеличении k график становится круче. Значение k представляет собой угловой коэффициент прямой и равно тангенсу угла наклона рассматриваемой прямой к положительному направлению оси X:
При использовании k < 0, можно наблюдать убывание линейной функции. Заметим, что в данном случае угол α — тупой и tg α < 0.
При k = 0, на графике будет изображена прямая y = b, которая параллельна оси X. В том случае, когда имеет место равенство угловых коэффициентов прямых, прямые будут параллельны друг другу.
Квадратичная функция \(y = ax2 + bx + c\) представляет собой параболу. Она обладает рядом особенностей:
- При a > 0, ветви параболы направлены вверх, при a < 0 — вниз.
- Формулы для вычисления координат, которые соответствуют вершине параболы:
- Точки пересечения параболы с осью X вычисляют, как корни квадратного уравнения \(ax^{2} + bx + c = 0\).
- При отсутствии корней или дискриминанте, который меньше нуля, парабола и ось Х не пересекаются.
- Точку пересечения параболы с осью Y можно определить, подставив в ее уравнение \(x = 0\).
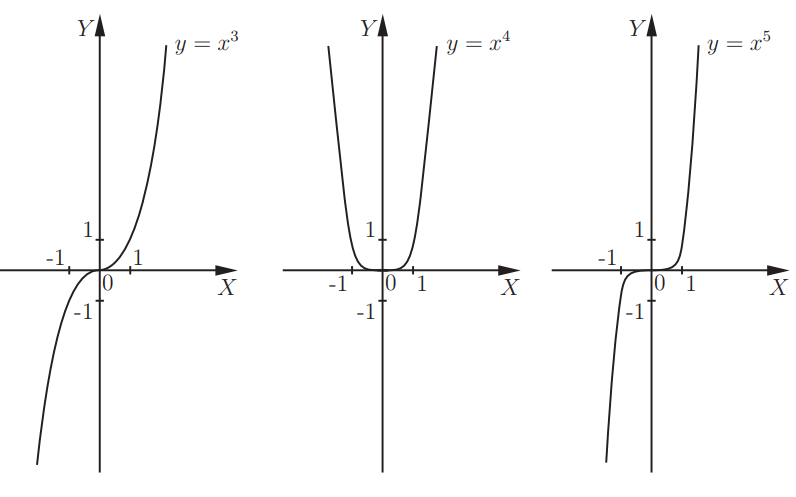
Функция \(y = x^{3}\) является кубической параболой. Можно представить ее на рисунке, а также функции\( y = x^{4}\) и \(y = x^{5}.\)
Можно отметить, что функции \(y = x^{2}\) и \(y = x^{4}\) обладают некоторыми сходствами. Графики являются симметричными по отношению к оси Y. В данном случае можно сказать, что рассматриваемые функции – четные.
Функция \(y = f(x)\) является четной, когда:
- область определения функции симметрична относительно нуля;
- каждое значение x из области определения соответствует справедливому равенству \(f(−x) = f(x)\).
Графики функций \(y = x^{3}\) и \(y = x^{5}\) симметричны по отношению к началу координат. Данные функции являются нечетными.
Функция \(y = f(x)\) – нечетная, при условии, что:
- область определения функции симметрична относительно нуля;
- любой x из области определения соответствует равенству \(f(-x) = -f(x)\).
Можно заметить, что функция \(y = x^{a}\) четная при четных значениях α и нечетная при нечетных α.
Функция \(\small y = \frac{1}{x}\) в виде гиперболы также представляет собой степенную функцию. Это объясняется тем, что \(\small \frac{1}{x} = x^{-1}\). Так как знаменатель не должен быть равен нулю, рассматриваемая функция не определена при \(x = 0\). Гипербола представляет собой нечетную функцию с графиком, который симметричен по отношению к началу координат.
Источник: ege-study.ru
Построение графика функции \(\small y = \sqrt{x}\) следует начинать с области определения. Выражение \(\small \sqrt{x}\) определено при \(x ≥ 0\). Поэтому областью определения функции являются все неотрицательные числа. Также \(\small y = \sqrt{x}\) принимает только неотрицательные значения, поскольку \(\small \sqrt{x} ≥ 0.\)
Целесообразно воспользоваться данными свойствами в процессе решения уравнений и неравенств. Уравнение вида \(\small \sqrt{f(x)}=g(x)\) имеет смысл только при \(f(x) ≥ 0\) и \(g(x) ≥ 0\). Это является областью допустимых значений.
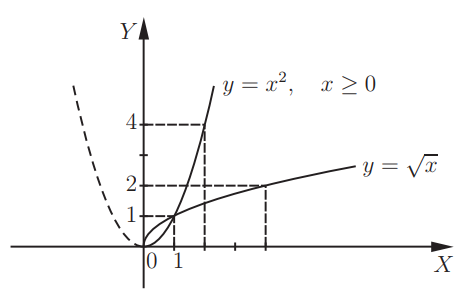
На одном графике можно построить параболу\( y = x^{2}\) и функцию \(\small y = \sqrt{x}\). Следует рассмотреть правую ветвь параболы, при \(x ≥ 0\). Заметим, что эта часть параболы и график функции \(\small y = \sqrt{x}\) словно нарисованы по одному шаблону, по-разному расположенному в координатной плоскости. Они симметричны относительно прямой y = x.
То, что для одной из них является областью определения, для другой — представляет собой область значений. Данные функции носят название взаимно-обратных.
Виды и их свойства, область определения
Степенные функции обладают рядом специфических свойств, которые могут отличаться в зависимости от их вида. Рассмотрим основные из них.
Свойства функции\( y=x^{\frac{m}{n}}, (m>n)\):
- D(y)=[0;+∞);
- функцию нельзя отнести ни к четной, ни к нечетной;
- возрастает на [0;+∞);
- не имеет ограничений в верхней части, но ограничена в нижней;
- отсутствует максимальное значение, минимальное значение равно нулю;
- непрерывность;
- E(f)=[0; +∞);
- выпукла вниз.
В качестве примера можно рассмотреть случай, когда показатель степени является правильной дробью, у которой значение числителя меньше, чем знаменателя. График функции\( y=x^{\frac{m}{n}}\), \((m>n)\) напоминает график функции \(y=\sqrt[n]{x}\):
Свойства функции\( y=x^{\frac{m}{n}}\), \(0<\frac{m}{n}<1:\)
- D(y)=[0;+∞);
- нельзя отнести ни к четной, ни к нечетной;
- возрастает на [0;+∞);
- не имеет ограничений сверху, ограничена снизу;
- максимальное значение отсутствует, наименьшее значение равно нулю;
- непрерывность;
- E(f)=[0; +∞);
- выпукла вверх.
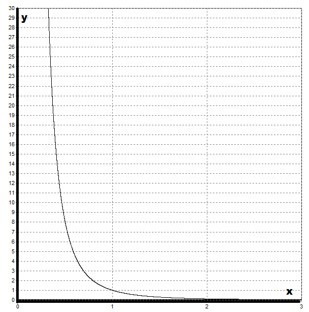
Далее следует ознакомиться с графиком функции \(y=x^{-\frac{m}{n}}\). Можно заметить, что он похож на гиперболу. График обладает двумя асимптотами:
- горизонтальной y=0;
- вертикальной х=0.
График имеет следующий вид:
Свойства функции \(y=x^{-\frac{m}{n}}:\)
- D(y)=(0;+∞);
- не является ни четной, ни нечетной;
- убывает на (0;+∞);
- не ограничена в верхней части, обладает ограничением в нижней;
- максимальное значение отсутствует, минимальное – ноль;
- непрерывность;
- E(f)=(0; +∞);
- выпукла вниз.
В том случае, когда x>0, а r – какое-либо рациональное число, производная степенной функции \(y=x^r\) определяется, согласно формуле:
\(y'=r*x^{r-1}\)
К примеру: \((x^{1000})'=1000x^{999} \)
\((x^{-8})'=-8x^{-9}\)
\(\frac{2}{(x^3)'}=\frac{2}{3}*x^{-\frac{1}{3}}\)
\((\sqrt[6]{(2x+5)^5})'=((2x+5)^{\frac{5}{6}})'=2*\frac{5}{6}(2x+5)^{-\frac{1}{6}}=\frac{5}{3}(2x+5)^{-\frac{1}{6}}.\)
Степенная функция с рациональным и иррациональным показателем
Степень действительного числа a, обладающего рациональным показателем n вычисляется, согласно уравнению:
\(a^{r}=\sqrt[n]{a^{m}}\)
Функция\( f(x)=x^{r}(r\in Q)\) представляет собой степенную функцию с рациональным показателем.
Степенью числа a, которое является положительным, c иррациональным показателем \(\alpha\) называется выражение вида \(a^{\alpha}\) со значением, равным пределу последовательности \(a^{\alpha_{0}}\), \(a^{\alpha_{1}}, a^{\alpha_{2}}\), …, где \(\alpha_{0}, \alpha_{1}, \alpha_{2}\) являются последовательными десятичными приближениями иррационального числа \(\alpha\).
Функция \(f(x)=x^{r}(r\in J)\) представляет собой степенную функцию с иррациональным показателем.
Как строить графики степенных функций
График функции является множеством точек, у которых абсциссы являются допустимыми значениями аргумента х, а ординаты – соответствующими значениями функции y.
Согласно определению, построить график какой-либо функции можно путем поиска всех пар соответствующих значений аргумента и функции. Как правило, в результате получается бесконечное множество точек, что затрудняет процесс построения графика. В связи с этим требуется исследовать функцию:
- обозначить область определения и область изменения функции;
- найти области ее убывания или возрастания;
- определить асимптоты, интервалы знакопостоянства;
- выявить несколько точек, принадлежащих графику;
- соединить найденные точки плавной кривой.
Задачи со степенной функцией
Необходимо определить максимальное и минимальное значения для функции \(y=x^{\frac{5}{2}}\) на отрезке:
- [1;16];
- (2,10);
- на луче [9;+∞).
Решение
Показатель степени рассматриваемой функции обладает положительным значением. В этом случае, учитывая свойства записанной функции, можно заключить, что она возрастает на всей области определения. Таким образом, функция достигает своего максимума и минимума на концах заданных отрезков (если она определена в этих точках).
\(y_{наим.}=1^{\frac{2}{5}}=1; y_{наиб.}=16^{\frac{5}{2}}=(\sqrt{16})^5=4^5=1024\)
На промежутке (2,10) максимальное и минимальное значения функции отсутствуют, в связи с тем, что промежуток является открытым, и точки 0 и 4 к данному интервалу не относятся.
На луче [9;+∞) наибольшее значение отсутствует
\(y_{наим.}=9^{\frac{5}{2}}=\sqrt{9^5}=(\sqrt{9})^5=3^5=243.\)
Требуется определить максимальное и минимальное значение на отрезке [1;9] для функции:
\(y=\frac{16}{5}x^{\frac{5}{2}}-\frac{1}{4}x^4\)
Решение
Вычислим производную рассматриваемой функции:
\(y'=\frac{16}{5}*\frac{5}{2}x^{\frac{3}{2}}-x^3=8x^{\frac{3}{2}}-x^3=8\sqrt{x^3}-x^3\)
Так как производная существует на всей области определения исходной функции, можно заключить, что критические точки отсутствуют.
Далее определим стационарные точки:
\(y'=8\sqrt{x^3}-x^3=0\)
\(8*\sqrt{x^3}=x^3\)
\(64x^3=x^6\)
\(x^6-64x^3=0\)
\(x^3(x^3-64)=0\)
\(x_1=0 и x_2=\sqrt[3]{64}=4\)
Заданному отрезку принадлежит только одно решение \(x_2=4\)
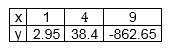
Построим таблицу значений нашей функции на концах отрезка и в точке экстремума:
Ответ: \(y_{наим.}=-862,65\) при\( x=9\); \( y_{наиб.}=38,4\) при \(x=4.\)
Решить уравнение: \(x^{\frac{4}{3}}=24-x\)
Решение
График функции \(y=x^{\frac{4}{3}}\) будет возрастать, а график функции \(у=24-х\) – убывать. Известно, что когда одна функция возрастает, а вторая убывает, то будет лишь одна точка, в которой эти функции пересекаются. Следовательно, уравнение обладает всего одним решением. Можно заметить, что:
\(8^{\frac{4}{3}}=\sqrt[3]{8^4}=(\sqrt[3]{8})^4=2^4=16\)
24-8=16
Таким образом, при х=8 уравнение преобразуется в справедливое равенство: 16=16, что является ответом к задаче.
Ответ: х=8.
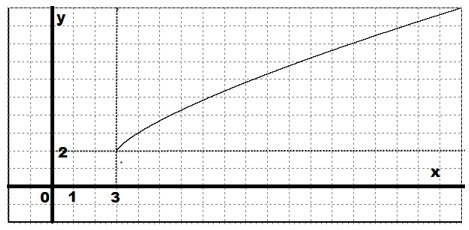
Необходимо построить график функции с объяснениями: \(y=(x-3)^\frac{3}{4}+2\)
Решение
График рассматриваемой функции можно получить из графика функции:
\(y=x^{\frac{3}{4}}\)
Требуется сместить этот график на 3 единицы в правую сторону и на 2 единицы вверх:
Требуется записать уравнение для касательной к прямой \(y=x^{-\frac{4}{5}}\) в точке х=1.
Решение
Обозначение уравнения касательной:
\(y=f(a)+f'(a)(x-a).\)
По условию задачи число a является натуральным числом 1, поэтому:
\(f(a)=f(1)=1^{-\frac{4}{5}}=1\)
Определим производную:
\(y'=-\frac{4}{5}x^{-\frac{9}{5}}\)
Таким образом:
\(f'(a)=-\frac{4}{5}*1^{-\frac{9}{5}}=-\frac{4}{5}.\)
Запишем уравнение касательной:
\(y=1-\frac{4}{5}(x-1)=-\frac{4}{5}x+1\frac{4}{5}\)
Ответ: \(y=-\frac{4}{5}x+1\frac{4}{5}.\)
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так