Стереометрия

Что такое стереометрия

Если основными фигурами планиметрии являются точка и прямая, то в стереометрии к изучению добавляется плоскость.

Примеры стереометрических фигур:

• шар;
• сфера;
• конус;
• цилиндр;
• призма и так далее.

Нередко основным способом решения задач в стереометрии является рассмотрение разнообразных плоскостей при выполнении планиметрических законов.

В стереометрии используются следующие обозначения: 

• прописные буквы A,B,C,D обозначают точки;
• строчные буквы обозначают прямые, например, AB = a; 
• плоскости, как правило, обозначаются такими буквами как \(\alpha,\;\beta,\;\gamma\) и подобными;
• принадлежность точек к прямой или точек и прямых к плоскости обозначается стандартно: \(A\;\in\;a\) или \(b\;\in\;\alpha.\)

Базовые теоремы, аксиомы и определения стереометрии

Сечения многогранников

При решении задач по стереометрии нередко придется строить сечения многогранников на определенной плоскости. Далее приведены базовые определения, которые относятся к сечению.

Сечением пирамиды, куба, параллелепипеда или же призмы будет являться фигура, которая состоит из всех точек, являющихся общими фигуры и секущей плоскости.

Секущая плоскость будет пересекать грани пирамиды, куба, параллелепипеда или же призмы по отрезкам, исходя из этого, сечение является многоугольником, который лежит в секущей плоскости, со сторонами — указанными отрезками.

Чтобы построить сечение указанных выше фигур стереометрии, необходимо построение точек пересечения секущей плоскости и ребер фигуры, а после соединяться каждые две из них, которые лежат в одной грани.

Симметрия фигур

1. Точки A и B будут являться симметричными относительно точки O в тех случаях, когда O — середина отрезка AB.
2. Точки A и B будут являться симметричными относительно прямой C в тех случаях, когда прямая C будет проходить через середину отрезка AB и будет ему перпендикулярна.
3. Точки A и B будут являться симметричными относительно плоскости \(\beta\) в тех случаях, когда плоскость α будет проходить через середину отрезка AB и будет ему перпендикулярна.
4. Точка О (прямая c, плоскость \(\beta\)) будет являться центром симметрии фигуры в тех случаях, когда все точки фигуры симметричны относительно точки O (прямой C, плоскости \(\beta\)) какой-либо точке этой же фигуры.
5. Выпуклый многогранник будет являться правильным в тех случаях, когда все его грани — равные между собой правильные многоугольники и в каждой вершине сходится одно и то же количество ребер.

Взаимное расположение прямых в пространстве

В пространстве прямые лежат либо в одной плоскости, либо в разных плоскостях.

1. Две прямые в пространстве будут являться параллельными в тех случаях, когда они лежат в одной и той же плоскости и не имеют общих точек.
2. Две прямые в пространстве будут являться пересекающимися в тех случаях, когда они лежат в одной и той же плоскости и имеют общую точку.
3. Две прямые в пространстве будут являться скрещивающимися в тех случаях, когда они не лежат в одной и той же плоскости.

Расстояние между фигурами

1. Расстоянием между фигурами будет называться самое маленькое среди расстояний между их точками.
2. Расстояние между двумя прямыми, которые скрещиваются, будет соответствовать величине отрезка с концами на этих прямых, который перпендикулярен им обеим. Для каждых двух скрещивающихся прямых такой отрезок существует и единственен.
3. Расстояние между двумя прямыми, которые скрещиваются, будет равняться расстоянию между параллельными плоскостями, в которых они лежат.
4. Расстояние между двумя прямыми, которые скрещиваются, будет равняться расстоянию от одной из них до параллельной ей плоскости, которая проходит через вторую прямую.
5. Расстояние между двумя прямыми, которые скрещиваются, будет равняться расстоянию между их проекциями на плоскость, которая перпендикулярна одной из них.

Основные теоремы стереометрии

Теоремы о параллельности прямых и плоскостей

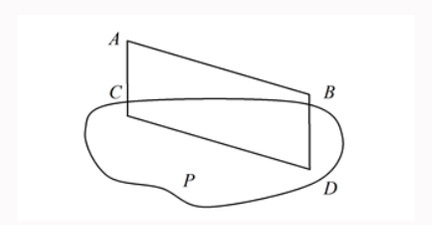
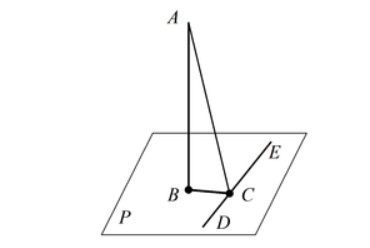
1. Если прямая AB параллельна какой-нибудь прямой CD, расположенной в плоскости P, то она параллельна самой плоскости.

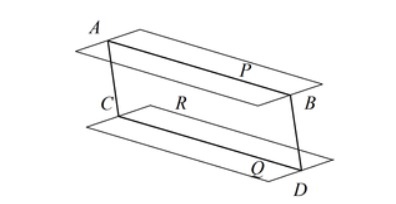
2. Если плоскость R проходит через прямую AB, параллельную другой плоскости P, и пересекает эту плоскость, то линия пересечения CD параллельна первой прямой AB.

3. Если две параллельные плоскости P и Q пересекаются третьей плоскостью R, то линии пересечения AB и CD параллельны.

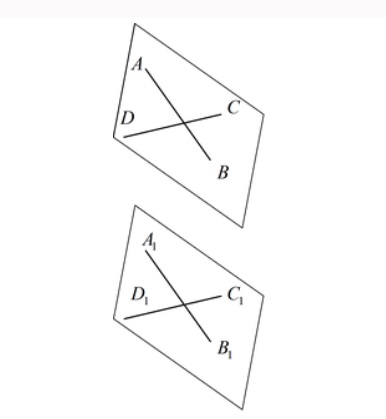
4. Если две пересекающиеся прямые AB и DC одной плоскости соответственно параллельны двум прямым A₁B₁ и C₁D₁ другой плоскости, то эти плоскости параллельны.

Теоремы о перпендикулярности прямых и плоскостей

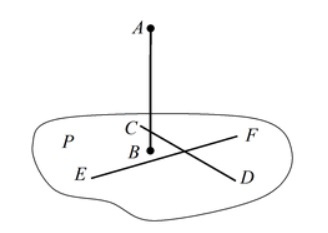
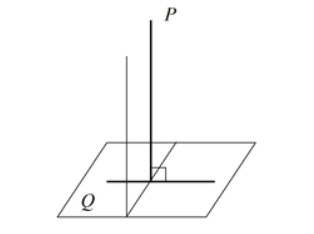
1. Для того что бы прямая AB была перпендикулярна плоскости P, необходимо и достаточно, чтобы она была перпендикулярна двум произвольным непараллельным прямым CD и EF, лежащим в этой плоскости.

2. Для того, чтобы прямая DE проведенная на плоскости P через основание наклонной AC была ей перпендикулярна, необходимо и достаточно, чтобы эта прямая была перпендикулярна к проекции BC, наклонной на плоскость P (достаточное условие этой теоремы называется «Теоремой о трех перпендикулярах»: AC, BC, DE).

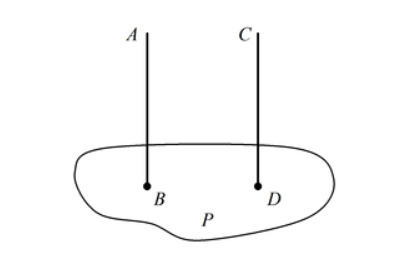
3. Если две прямые AB и CD перпендикулярны одной плоскости P, то они параллельны между собой.

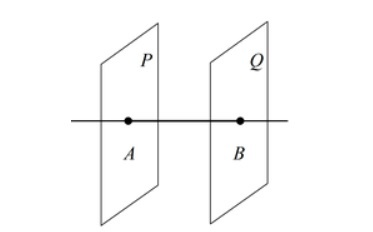
4. Если две плоскости P и Q перпендикулярны одной прямой AB, то они параллельны друг другу.

Теоремы о перпендикулярности плоскостей

1. Если плоскость P проходит через перпендикуляр к другой плоскости Q, то плоскость P перпендикулярна плоскости Q.

2. Если две плоскости P и Q взаимно перпендикулярны, то прямая, проведенная в одной плоскости перпендикулярно линии пересечения плоскостей, перпендикулярна другой плоскости.

Теорема о скрещивающихся прямых

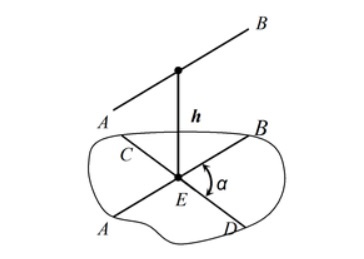
1. Угол \(\alpha\) между скрещивающимися прямыми AB и CD определяется как угол между одной из этих прямых (например, CD) и любой прямой A₁B₁, проходящей через ее произвольную точку E параллельно другой прямой.

2. Расстояние h между скрещивающимися прямыми AB и CD определяется как кратчайшее расстояние от одной из этих прямых и может быть найдено как расстояние от одной их этих прямых (например, AB) до плоскости P, проходящей через другую прямую CD параллельно первой.

Основные аксиомы стереометрии

Рассмотрим четыре основные аксиомы стереометрии. 

1. Через любые три точки, не лежащие на одной прямой, проходит плоскость, и при том только одна.
2. Если две точки прямой лежат в плоскости, то каждая точка данной прямой лежит в этой плоскости. В таком случае говорят, что прямая лежит в плоскости или, что плоскость проходит через прямую.
3. Если две плоскости имеют общую точку, то они имеют общую прямую, которой принадлежат все общие точки этих плоскостей. Тогда считается, что плоскости пересекаются по прямой.
4. В любой плоскости пространства выполняются все аксиомы планиметрии. То есть для любой плоскости пространства справедливы все доказанные теоремы и формулы из планиметрии.

Дополнительные аксиомы стереометрии

1. Для любой плоскости в пространстве существуют точки, которые принадлежат данной плоскости и точки, которые не принадлежат ей.
2. Две различные плоскости, которые имеют одну общую точку, будут пересекаться по прямой, проходящей через эту точку.
3. Через две различные прямые, которые имеют общую точку, может быть проведена только одна плоскость.

Следствия из аксиом стереометрии

1. Через прямую и не лежащую на ней точку проходит плоскость и притом только одна.
2. Через две пересекающиеся прямые проходит плоскость и притом только одна.
3. Через две параллельные прямые проходит плоскость и притом только одна.
4. Из аксиомы 2 следует, что прямая, не лежащая в плоскости, не может иметь с плоскостью более одной общей точки. Если прямая и плоскость имеют только одну общую точку, то говорят, что прямая пересекает плоскость.

Основные стереометрические фигуры

1. Многогранник — геометрическое тело, которое является ограниченным количеством плоских многоугольников. Если взять два любых плоских многоугольника, имеющих сторону, то можно заметить, что они не будут лежащими в одной плоскости. Эти многоугольники носят называние граней, их стороны — ребра многогранника, а их вершины — вершины многогранника. Фигура, которую образовывают все грани многогранника, носит называния полная поверхность. Площадь полной поверхности можно вычислить, сложив площади всех граней.
2. Кубом называется многогранник, который имеет шесть граней, и все они — равные квадраты.
3. У параллелепипеда есть шесть граней, и все они являются параллелограммами. Ребра и вершины параллелепипеда определяются так же, как и в случае других многогранников. Противолежащие грани будут называться таковыми, если они не имеют общего ребра, в то время как грани с общим ребром носят название смежных. Возможна ситуация, в которой две противолежащие грани параллелепипеда окажутся выделенными и получат называние оснований. В этом случае все остальные грани станут боковыми, а их стороны — боковыми ребрами. При этом, параллелепипед, все боковые грани которого — прямоугольники, а не параллелограммы, будет называться прямым, а параллелепипед с гранями-прямоугольниками, будет называться прямоугольным.
4. Призма (n-угольная) в стереометрии представляет собой многогранник, две грани которого являются равными n-угольниками. Остальное же количество граней (n) является параллелограммами. Основаниями призмы будут равные n-угольники, в то время как боковыми гранями будут параллелограммы. Призма может быть также прямой. Такая призма обладает прямоугольниками в роли боковых граней. Правильной n-угольной призмой называется призма с прямоугольниками в роли боковых граней, а ее основаниями будут являться правильные n-угольники. Для определения площади боковой поверхности призмы (S_бок), необходимо сложить все площади боковых граней. А для нахождения площади поверхности призмы (S_полн) понадобится сложить площади всех поверхностей. Объем (V) призмы будет определяться как произведение высоты (H) призмы на площадь снования (S_осн)
5. Пирамида (n-угольная) является многогранником с одной гранью в форме n-угольника, и остальными n гранями в форме треугольников с общей вершиной. В такой пирамиде n-угольник будет основанием, а треугольники, которые имеют общую вершину (вершина пирамиды) — боковыми гранями. Ребрами пирамиды называют стороны ее граней. n-угольная пирамида может являться правильной. В этом случае ее основание — это правильный n-угольник, равные между собой боковые ребра, в то время как боковые грани — равные между собой равнобедренные треугольники. Для нахождения площади боковой поверхности пирамиды (S_бок) необходимо найти сумму площадей боковых граней. В то время как площадь поверхности пирамиды (S_полн) определяется через сумму площадей всех граней пирамиды.
6. Тетраэдр — это по своей сути треугольная пирамида. Все ее грани являются прямоугольниками, равными между собой. Тетраэдр представляет собой частный случай правильной треугольной пирамиды. 
7. Двугранный угол — это фигура, которую образовывают две плоскости, имеющие общую граничную прямую и часть пространства, для которой полуплоскости будут являться границей. Линейным углом в таком случае будет называться угол со сторонами, представляющими собой лучи с общим началом на ребре двугранного угла. Эти лучи должны быть проведены в гранях угла перпендикулярно ребру.
8. Цилиндр представляет собой окружность с центром O и радиусом R, через все точки которой проведены прямые, перпендикулярные плоскости окружности. Цилиндрическая поверхность в данном случае будет фигурой, которую образовывают прямые — образующие цилиндрической поверхности. Все образующие являются параллельными друг другу и перпендикулярными плоскости окружности. Основаниями цилиндра являются два равных круга. Ось цилиндра — это отрезок, соединяющий центры оснований цилиндра. Высота цилиндра — это перпендикулярная прямая, проведенная из любой точки плоскости одного из оснований цилиндра к плоскости второго основания. 
9. Сферой называют замкнутую поверхность. Центром сферы будет являться точка, от которой равноудалены остальные точки, чье геометрическое место в пространстве также будет называться сферой. Сфера кроме этого называется телом вращения, которое образовано вращением полуокружности вокруг своего диаметра.