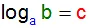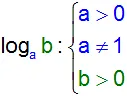Определение логарифма и его свойства

Что такое логарифм — понятие и определение

Благодаря логарифмам можно значительно упростить сложные алгебраические операции, к примеру, вместо умножения выполнить сложение, заменить возведение в степень умножением или делением. Таким образом, удобно решать громоздкие формулы. Для понимания метода применения логарифма можно рассмотреть практический пример. Предположим, что требуется найти решение следующего уравнения:

\(\displaystyle {{2}^{x}}=8\)

В начале следует определить степень, в которую можно возвести число 2, и в результате получить число 8. Решение подразумевает использование способа подбора чисел. Возводя 2 в степени, можно выяснить, что в третьей степени 2 равна 8. Вывод:

\((\displaystyle {{2}^{3}}=8)\)

В результате ответом к задаче будет число 3.

Разберем второй пример:

\(\displaystyle {{2}^{x}}=5\)

Использовать главный метод подбора, как в предыдущем уравнении, не получится, так как работать предстоит не с целыми и даже не с рациональными числами. В данном случае целесообразно оперировать понятием логарифма. Запись будет иметь следующий вид:

\(\displaystyle x={{\log}_{2}}5\)

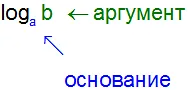
В общем виде логарифм записывают, таким образом: 

Основные свойства десятичных и натуральных логарифмов

Десятичный логарифм обозначают, как \(lg(a).\)

Примеры десятичных логарифмов:

1. \(log_{10}(100)= lg(100)=2\)
2. \(log_{10}(1000)=lg(1000)=3 \)
3. \(log_{10}(10)=lg(10)=1\)

Натуральный логарифм обозначают, как ln(x). В обозначении е является экспонентой, числом-константой, которое приблизительно равно 2,718281828459…. Данное число нередко применяют при решении математических задач и доказательстве закономерностей.

Примеры натуральных логарифмов:

1. \(log_{e}(e^2)=ln(e^2)=2\)
2. \(log_{e}(e)=ln(e)=1\)
3. \(log_{e}(e^5)=ln(e^5)=5\)

Свойства и правила, предусмотренные для обыкновенных логарифмов, распространяются также на натуральные и десятичные логарифмы. Все логарифмы обладают рядом свойств. Благодаря выведенным закономерностям, удается существенно упростить решение примеров и формул с помощью специальных преобразований и вычислений. Помимо рассматриваемых свойств, другие операции с логарифмами производить не представляется возможным. Свойства логарифмов:

\(\displaystyle \begin{array}{l}\text{ }1.\text{ }{{\log }_{a}}{{a}^{x}}=x\\\text{ }2.\text{ }{{\log }_{a}}b+{{\log }_{a}}c={{\log }_{a}}\left( b\cdot c \right)\\\text{ }3.\text{ }{{\log }_{a}}b-{{\log }_{a}}c={{\log }_{a}}\frac{b}{c}\\\left. \begin{array}{l}4.\text{ }{{\log }_{a}}{{b}^{n}}=n\cdot {{\log }_{a}}b\ \\5.\text{ }{{\log }_{{{a}^{n}}}}b=\frac{1}{n}\cdot {{\log }_{a}}b\end{array} \right|\Rightarrow \text{ }6.{{\log }_{{{a}^{n}}}}{{b}^{m}}=\frac{m}{n}\cdot {{\log }_{a}}b\\\text{ }7.\text{ }{{\log }_{a}}b=\frac{{{\log }_{c}}b}{{{\log }_{c}}a}\text{, }\left( c>0,\text{ }\ne \text{1} \right)\text{ }\Rightarrow \text{ }8.\text{ }{{\log }_{a}}b=\frac{1}{{{\log }_{b}}a},\text{ }\left( b\ne 1 \right).\end{array} \)

Доказательства тождеств

Свойство 1: степень аргумента можно записать таким образом:

\(\displaystyle {{\log }_{a}}{{a}^{x}}=x\)

В процессе доказательства предположим, что:

\(\displaystyle {{\log }_{a}}b=x, \ тогда \ \displaystyle {{a}^{x}}=b\)

Таким образом:

\(\displaystyle \frac{{{\log }_{c}}b}{{{\log }_{c}}a}=\frac{{{\log }_{c}}{{a}^{x}}}{{{\log }_{c}}a}=\frac{x{{\log }_{c}}a}{{{\log }_{c}}a}=x={{\log }_{a}}b\)

Тождество доказано.

Свойство 2: Сумма логарифмов, имеющих одинаковые основания, равна логарифму произведения:

\(\displaystyle {{\log }_{a}}b+{{\log }_{a}}c={{\log }_{a}}\left( b\cdot c \right)\)

При доказательстве следует предположить, что:

\(\displaystyle {{\log }_{a}}b=x, тогда \ \displaystyle {{a}^{x}}=b. Пусть \ \displaystyle {{\log }_{a}}c=y\)

В таком случае, получим:

\(\displaystyle {{a}^{y}}=c\)

Таким образом:

\(\displaystyle {{\log }_{a}}\left( b\cdot c \right)={{\log }_{a}}\left( {{a}^{x}}\cdot {{a}^{y}} \right)={{\log }_{a}}{{a}^{x+y}}\underset{\text{по правилу 1}}{\mathop{=}}\,x+y={{\log }_{a}}b+lo{{g}_{a}}c.\)

Доказательство представлено. Можно разобрать данное свойство на конкретном примере:

\(\displaystyle {{\log }_{3}}5+{{\log }_{3}}0,6\)

Решить уравнение можно так:

\(\displaystyle {{\log }_{3}}5+{{\log }_{3}}0,6={{\log }_{3}}\left( 5\cdot 0,6 \right)={{\log }_{3}}3=1\)

В процессе, применяя свойство логарифмов, была преобразована сумма логарифмов, но не разность, что мешает объединению данных логарифмов. Справедливо сделать наоборот, то есть «разбить» первый логарифм на пару. Упрощение будет иметь вид: \(\displaystyle {{\log }_{2}}80={{\log }_{2}}\left( 16\cdot 5 \right)={{\log }_{2}}\left( {{2}^{4}}\cdot 5 \right)={{\log }_{2}}{{2}^{4}}+{{\log }_{2}}5=4+{{\log }_{2}}5 \)

Подобнымм образом можно найти ответ на более сложные уравнения:

\(\displaystyle lo{{g}_{5}}250-{{\log }_{5}}2\)

Решение будет следующим:

\(\displaystyle {{\log }_{5}}250={{\log }_{5}}\left( 125\cdot 2 \right)={{\log }_{5}}\left( {{5}^{3}}\cdot 2 \right)={{\log }_{5}}{{5}^{3}}+{{\log }_{5}}2=3+{{\log }_{5}}2\)

Очевидно, что:

\(\displaystyle {{\log }_{5}}250-{{\log }_{5}}2=3+{{\log }_{5}}2-{{\log }_{5}}2=3\)

Приведемв качестве примера упрощение нескольких уравнений:

Свойство 3: Разность логарифмов, обладающих идентичными основаниями, равна логарифму частного:

\(\displaystyle lo{{g}_{a}}b-{{\log }_{a}}c={{\log }_{a}}\frac{b}{c}\)

Доказательство данного свойства схоже с подтверждением Свойства 2. Предположим, что:

\(\displaystyle {{\log }_{a}}b=x, тогда \ \displaystyle {{a}^{x}}=b\)

\(\displaystyle {{\log }_{a}}c=y, тогда \ \displaystyle {{a}^{y}}=c\)

Таким образом:

\(\displaystyle {{\log }_{a}}\left( \frac{b}{c} \right)={{\log }_{a}}\left( \frac{{{a}^{x}}}{{{a}^{y}}} \right)={{\log }_{a}}{{a}^{x-y}}=x-y={{\log }_{a}}b-{{\log }_{a}}c\)

\(\displaystyle {{\log }_{a}}b-{{\log }_{a}}c={{\log }_{a}}\left( \frac{b}{c}\cdot c \right)-{{\log }_{a}}c={{\log }_{a}}\frac{b}{c}+{{\log }_{a}}c-{{\log }_{a}}c={{\log }_{a}}\frac{b}{c}\)

Свойство доказано.

Если рассмотреть в данном контексте задачу из предыдущего примера, то его решение существенно упрощается:

\(\displaystyle {{\log }_{5}}250-{{\log }_{5}}2={{\log }_{5}}\frac{250}{2}={{\log }_{5}}125={{\log }_{5}}{{5}^{3}}=3\)

Можно найти решение более сложного уравнения:

\(\displaystyle \log _{2}^{2}2\sqrt{3}-\log _{2}^{2}\sqrt{3}-{{\log }_{2}}3\)

В данном случае целесообразно воспользоваться формулами сокращенного умножения. В уравнении есть разность квадратов:

\(\displaystyle \log _{2}^{2}2\sqrt{3}-\log _{2}^{2}\sqrt{3}=\left( {{\log }_{2}}2\sqrt{3}-{{\log }_{2}}\sqrt{3} \right)\left( {{\log }_{2}}2\sqrt{3}+{{\log }_{2}}\sqrt{3} \right)\)

Далее можно воспользоваться Свойством 2 и 3:

\(\displaystyle \log _{2}^{2}2\sqrt{3}-\log _{2}^{2}\sqrt{3}-{{\log }_{2}}3\)\(\displaystyle={{\log }_{2}}\frac{2\sqrt{3}}{\sqrt{3}}\cdot {{\log }_{2}}\left( 2\sqrt{3}\cdot \sqrt{3} \right)-{{\log }_{2}}3\)\(\displaystyle={{\log }_{2}}2\cdot {{\log }_{2}}\left( 2\cdot 3 \right)-{{\log }_{2}}3=1\cdot \left( 1+{{\log }_{2}}3 \right)-{{\log }_{2}}3=1\)

В качестве примеров можно представить упрощение следующих уравнений:

Решение:

\(\displaystyle {{\log }_{3}}4-{{\log }_{3}}12={{\log }_{3}}\frac{4}{12}={{\log }_{3}}\frac{1}{3}=-1\)

Решение:

\(\displaystyle {{\log }_{0,3}}3-{{\log }_{0,3}}10={{\log }_{0,3}}\frac{3}{10}=1\)

Решение:

\(\displaystyle {{\log }_{1,75}}28+{{\log }_{1,75}}2-{{\log }_{1,75}}32={{\log }_{1,75}}\frac{28\cdot 2}{32}={{\log }_{\frac{7}{4}}}\frac{7}{4}=1\)

Решение:

\(\displaystyle \lg \sqrt{0,05}-\lg \sqrt{5}=\lg \frac{\sqrt{0,05}}{\sqrt{5}}=\lg \sqrt{0,01}=\lg 0,1=-1\)

Решение:

\(\displaystyle {{\lg }^{2}}2\sqrt{5}-{{\lg }^{2}}5\sqrt{2}-\frac{3}{2}\lg \sqrt{\frac{2}{5}}\)\(\displaystyle=\left( \lg 2\sqrt{5}-\lg 5\sqrt{2} \right)\left( \lg 2\sqrt{5}+\lg 5\sqrt{2} \right)-\frac{3}{2}\lg \sqrt{\frac{2}{5}}\)\(\displaystyle=\lg \frac{2\sqrt{5}}{5\sqrt{2}}\cdot \lg \left( 2\sqrt{5}\cdot 5\sqrt{2} \right)-\frac{3}{2}\lg \sqrt{\frac{2}{5}}=\lg \sqrt{\frac{2}{5}}\cdot \lg {{10}^{\frac{3}{2}}}-\frac{3}{2}\lg \sqrt{\frac{2}{5}}\)

Свойство 4: В том случае, когда аргумент логарифма содержит степень, ее показатель легко вынести за знак логарифма.

\(\displaystyle {{\log }_{a}}{{b}^{n}}=n\cdot {{\log }_{a}}b\)

При доказательстве целесообразно воспользоваться определением логарифма. Предположим, что:

\(\displaystyle {{\log }_{a}}b=x, тогда\ \displaystyle {{a}^{x}}=b\)

Таким образом: \(\displaystyle {{\log }_{a}}{{b}^{n}}={{\log }_{a}}{{\left( {{a}^{x}} \right)}^{n}}={{\log }_{a}}{{a}^{nx}}=nx=n\cdot {{\log }_{a}}b\)

В итоге свойство доказано. Данную закономерность можно представить так:

\(\displaystyle {{\log }_{a}}{{b}^{n}}={{\log }_{a}}\left( \underbrace{b\cdot b\cdot ...\cdot b}_{n\text{ раз}} \right)\text{ }\underset{\text{правило}\ \text{2}}{\mathop{=}}\,\text{ }\underbrace{{{\log }_{a}}b+lo{{g}_{a}}b+...+{{\log }_{a}}b}_{n\text{ раз}}=n\cdot {{\log }_{a}}b\)

Таким образом, степень аргумента переносят вперед логарифма в виде коэффициента.

Разобрать правило можно на примере поиска ответа на уравнение:

\(\displaystyle \frac{{{\log }_{2}}25}{{{\log }_{2}}5}\)

Решение будет иметь следующий вид:

\(\displaystyle \frac{{{\log }_{2}}25}{{{\log }_{2}}5}=\frac{{{\log }_{2}}{{5}^{2}}}{{{\log }_{2}}5}=\frac{2{{\log }_{2}}5}{{{\log }_{2}}5}=2\)

Рассмотрим разные формы применения Свойства 4.

Решение:

\(\displaystyle \frac{{{\log }_{2}}81}{{{\log }_{2}}3}=\frac{{{\log }_{2}}{{3}^{4}}}{{{\log }_{2}}3}=4\)

Решение:

\(\displaystyle \frac{{{\log }_{3}}125}{{{\log }_{3}}625}=\frac{{{\log }_{3}}{{5}^{3}}}{{{\log }_{3}}{{5}^{4}}}=\frac{3{{\log }_{3}}5}{4{{\log }_{3}}5}=\frac{3}{4}=0,75\)

Решение:

\(\displaystyle \frac{\log _{5}^{2}25\sqrt{10}-\log _{5}^{2}\sqrt{10}}{{{\log }_{5}}250}\)\(\displaystyle=\frac{{{\log }_{5}}\left( 25\sqrt{10}\cdot \sqrt{10} \right)\cdot \log \frac{25\sqrt{10}}{\sqrt{10}}}{{{\log }_{5}}250}=\frac{{{\log }_{5}}250\cdot {{\log }_{5}}{{5}^{2}}}{{{\log }_{5}}250}=2\)

Свойство 5: В том случае, когда основание логарифма представляет собой степень, ее показатель представляется возможным убрать за знак логарифма:

\(\displaystyle {{\log }_{{{a}^{n}}}}b=\frac{1}{n}\cdot {{\log }_{a}}b.\)

В процессе доказательства свойства можно предположить, что:

\(\displaystyle {{\log }_{a}}b=x, тогда \ \displaystyle {{a}^{x}}=b\)

В таком случае:

\(\displaystyle {{\log }_{{{a}^{n}}}}b={{\log }_{{{a}^{n}}}}{{a}^{x}}={{\log }_{{{a}^{n}}}}{{a}^{\frac{x\cdot n}{n}}}={{\log }_{{{a}^{n}}}}{{\left( {{a}^{n}} \right)}^{\frac{x}{n}}}=\frac{x}{n}=\frac{1}{n}\cdot {{\log }_{a}}b\)

Свойство доказано.

Свойство 6: В том случае. когда основание и аргумент логарифма содержат степени, показатели данных степеней можно вынести за знак логарифма:

\(\displaystyle {{\log }_{{{a}^{n}}}}{{b}^{m}}=\frac{m}{n}\cdot {{\log }_{a}}b\)

Свойство справедливо и в том случае, когда степени одинаковые:

\(\displaystyle {{\log }_{{{a}^{n}}}}{{b}^{n}}={{\log }_{a}}b\)

Свойство 7: В том случае, когда основания логарифмов неодинаковые, то для дальнейшего решения уравнения целесообразно привести логарифмы к одному основанию:

\(\displaystyle {{\log }_{a}}b=\frac{{{\log }_{c}}b}{{{\log }_{c}}a}\text{ }\left( c>0;\text{ }\ne \text{1} \right)\)

Предположим, что:

\(\displaystyle {{\log }_{a}}b=x, тогда \ \displaystyle {{a}^{x}}=b\)

Таким образом:

\(\displaystyle \frac{{{\log }_{c}}b}{{{\log }_{c}}a}=\frac{{{\log }_{c}}{{a}^{x}}}{{{\log }_{c}}a}=\frac{x{{\log }_{c}}a}{{{\log }_{c}}a}=x={{\log }_{a}}b\)

В результате свойство доказано.

Свойство 8: Основание и аргумент логарифма допустимо переставлять. В результате выражение будет «перевернутым», то есть логарифм встанет на место знаменателя:

\(\displaystyle {{\log }_{a}}b=\frac{1}{{{\log }_{b}}a},\text{ }\left( b\ne 1 \right).\)

Данная закономерность является частным случаем Свойства 7. При подстановке выражения:

\(\displaystyle c=b\)

В результате получим:

\(\displaystyle {{\log }_{a}}b=\frac{{{\log }_{b}}b}{{{\log }_{b}}a}=\frac{1}{{{\log }_{b}}a}.\)

Свойство доказано.

В качестве примера рассмотрим решение распространенных математических задач.

Решение:

В данном случае целесообразно применить Свойство 2:

\(\displaystyle {{\log }_{5}}75+{{\log }_{5}}\frac{1}{3}={{\log }_{5}}\left( 75\cdot \frac{1}{3} \right)={{\log }_{5}}25=2\)

Ответ: 2

Решение:

Благодаря упрощению выражения с использованием Свойства 3 и 4, получим:

\(\displaystyle lo{{g}_{3}}36-2\overbrace{{{\log }_{3}}2={{\log }_{3}}36-lo{{g}_{3}}{{2}^{2}}}^{\text{по}\ \text{правилу}\ \text{4}}\underset{\text{по}\ \text{правилу 3}}{\mathop{=}}\,\text{ }{{\log }_{3}}\frac{36}{4}={{\log }_{3}}9=2\)

Ответ: 2

 

Решение

В данном случае необходимо воспользоваться Свойством 7 и перейти к основанию 2:

\(\displaystyle {{\log }_{8\sqrt[5]{4}}}\left( 32\sqrt[5]{2} \right)=\frac{{{\log }_{2}}\left( 32\sqrt[5]{2} \right)}{{{\log }_{2}}\left( 8\sqrt[5]{4} \right)}\underset{правило 2}{\mathop{=}}\,\frac{{{\log }_{2}}32+{{\log }_{2}}\sqrt[5]{2}}{{{\log }_{2}}8+lo{{g}_{2}}\sqrt[5]{4}}\)\(\displaystyle=\frac{{{\log }_{2}}{{2}^{5}}+{{\log }_{2}}{{2}^{\frac{1}{5}}}}{{{\log }_{2}}{{2}^{3}}+{{\log }_{2}}{{2}^{\frac{2}{5}}}}\underset{правило 1}{\mathop{=}}\,\frac{5+\frac{1}{5}}{3+\frac{2}{5}}=\frac{26}{17}\)

Ответ: \(\frac{26}{17}\)

Решение:

\(\displaystyle \frac{\log _{5}^{2}25\sqrt{10}-\log _{5}^{2}\sqrt{10}}{{{\log }_{5}}250}\)\(\displaystyle=\frac{{{\log }_{5}}\left( 25\sqrt{10}\cdot \sqrt{10} \right)\cdot \log \frac{25\sqrt{10}}{\sqrt{10}}}{{{\log }_{5}}250}=\frac{{{\log }_{5}}250\cdot {{\log }_{5}}{{5}^{2}}}{{{\log }_{5}}250}=2\)

 

Как посчитать логарифм, операции, все формулы

Логарифм представляет собой степень, в которую необходимо возвести основание, чтобы получить аргумент. На калькуляторе расчет будет иметь следующий вид:  \(2,321928\ldots\) и т.д. Данное число является иррациональным. По-другому выражение можно записать так:

\(\displaystyle {{\log }_{2}}5\)

Второй случай значительно удобнее, чем первое выражение. Произношение такого значения: «Решением уравнения два в степени икс равно пяти является логарифм по основанию два от пяти».

Степень числа и логарифма в любом случае имеет основание, которое расположено внизу. Вверху у степени есть показатель, а у логарифма – аргумент. Уравнение:

\(\displaystyle {{2}^{3}}=8\)

записывают в таком виде:

\(\displaystyle {{\log }_{2}}8=3\)

Прочитать полученное равенство можно так: «Логарифм по основанию два от восьми равен трем».

Обобщенная запись:

Читаться данное выражение будет так: «Логарифм по основанию a от b равен c»,

и означает: «Чтобы получить число b, нужно число a возвести в степень c»:

По-другому,\( \displaystyle {{\log }_{a}}b\) является степенью, в которую нужно возвести a, чтобы получить b.

Решение:

\(\displaystyle {{\log }_{2}}4=2\), так как число 2 нужно возвести в степень 2, чтобы получить 4

Решение

Исходя из того, что: \(\displaystyle 8={{2}^{3}}\)

Получим:

\(\displaystyle \frac{1}{8}=\frac{1}{{{2}^{3}}}={{2}^{-3}}\)

Таким образом, 2 нужно возвести в степень -3, чтобы получить \(\displaystyle \frac{1}{8}\)

В результате:

\(\displaystyle {{\log }_{2}}\frac{1}{8}=-3\)

В данном случае нужно рассмотреть основание. Есть ли при этом возможность представить 0,25 в виде 2 в определенной степени. Следует записать число, как обычную дробь:

\(\displaystyle 0,25=\frac{1}{4}=\frac{1}{{{2}^{2}}}={{2}^{-2}}\)

Таким образом:

\(\displaystyle {{\log }_{2}}0,25=-2\)

Не во всех случаях представляется возможным подобрать нужную степень. Тогда целесообразно представить ответ в виде логарифма. Оставить такое решение без изменений не корректно. Следует выполнить ряд преобразований. Для этого выражение упрощают и записывают, как иррациональное число. При этом необходимо учитывать область допустимых значений переменных или ОДЗ. Существуют определенные ограничения:

Таким образом, согласно правилам, значение аргумента и основания должно быть больше нуля, а основание не должно быть равно 1. Данные положения достаточно просто доказать. Предположим, что a=1. В этом случае логарифм не будет существовать по причине того, что число 1, возведенное в любую степень, будет равно 1. Кроме того:

\(\displaystyle {{\log }_{1}}b\) не существует ни при каком \(\displaystyle b\ne 1\)

Однако:\( \displaystyle {{\log }_{1}}1\) может принимать любые значения.

В связи с этим, объект не интересен в плане решения уравнений и не применяется в математике. Аналогичная ситуация с a=0. При этом 0 в любой положительной степени равен 0. В отрицательную степень 0 возводить нельзя, так как недопустимо делить на ноль.

Если a<0, то станет проблематично возвести число в дробную степень, которая будет записываться, как корень:

\(\displaystyle {{a}^{\frac{m}{n}}}=\sqrt[n]{{{a}^{m}}}\)

К примеру, выражение не будет существовать:

\(\displaystyle {{\log }_{4}}2=\frac{1}{2} (то \ есть \ \displaystyle {{4}^{\frac{1}{2}}}=\sqrt{4}=2), а \ вот \ \displaystyle {{\log }_{-4}}2\)

В связи с этим, с отрицательными основаниями не принято работать при решении уравнений. Так как основание а является положительным, то при возведении его в любую степень получается также положительное число. Таким образом, аргумент должен соответствовать положительному значению. К примеру:

\(\displaystyle {{\log }_{2}}\left( -4 \right)\) не будет существоаать по причине, что 2 ни в какой степени не будет отрицательным числом (и даже нулем, поэтому \(\displaystyle {{\log }_{2}}0\) тоже не существует).

Начинать решение задач на логарифмы следует с записи ОДЗ. Например, дано уравнение:

\(\displaystyle {{\log }_{x}}\left( x+2 \right)=2\)

Согласно определению, логарифм \(\displaystyle {{\log }_{x}}\left( x+2 \right)\) представляет собой степень, в которую необходимо возвести основание х, чтобы получить аргумент \(\displaystyle \left( x+2 \right)\)

Согласно условию задачи, степень равна 2:

\(\displaystyle {{x}^{2}}=x+2\)

В результате можно записать стандартное квадратное уравнение в виде:

\(\displaystyle {{x}^{2}}-x-2=0\)

Решить данное выражение целесообразно с помощью теоремы Виета: корни в сумме составляют 1, а произведение равно -2. Подбором получим числа 2 и -1. Одновременно два этих ответа предлагать недопустимо. При подстановке корней в начальное уравнение получим:

\(\displaystyle x=2\text{: }{{\log }_{2}}\left( 2+2 \right)={{\log }_{2}}4=2\)

Данное равенство справедливо.

\(\displaystyle x=-1\text{: }{{\log }_{-1}}\left( -1+2 \right)=2\)

В этом случае запись неверна, так как основание не может быть отрицательным, то есть корень \(x=-1\)  является «сторонним».

Исключить подобные ответы можно, если записывать ОДЗ на первом шаге решения уравнений:

\(\displaystyle \left\{ \begin{array}{l}x>0\\x\ne 1\\x+2>0\end{array} \right.\text{ }\Leftrightarrow \text{ }\left\{ \begin{array}{l}x>0\\x\ne 1.\end{array} \right.\)

Таким образом, при расчете корней \(x=2 \ и \ x=-1\), можно сразу исключить корень -1, и записать правильный ответ.

Наиболее простым логарифмическим уравнением является уравнение в виде:

\(\displaystyle lo{{g}_{a}}~x~=~b\)

Решить какое-либо логарифмическое уравнение можно с помощью приведения его к виду:

\(\displaystyle lo{{g}_{a}}\left( f\left( x \right) \right)~=~lo{{g}_{a}}\left( g\left( x \right) \right)\)

Далее выполняют преобразования полученного равенства для получения уравнения без логарифмов:

\(\displaystyle f\left( x \right)=g\left( x \right)\)

 

В процессе решения логарифмических уравнений используют несколько основных методов:

На основании определения логарифма:\( \displaystyle lo{{g}_{a}}~f(x)=b\ \Leftrightarrow \ ~f(x)={{a}^{b}},\ \ \ a>0,\ a\ne 1\)

Применение свойств логарифма

Ввод новой переменной: при замещении\( \displaystyle lo{{g}_{a}}x~=~t\) можно упростить логарифмическое уравнение относительно t

Переход на новое основание:\( \displaystyle {{\log }_{a}}b=\frac{{{\log }_{c}}b}{{{\log }_{c}}a}\text{ }\left( c>0;\text{ }\ne \text{1} \right) получим \ \displaystyle {{\log }_{a}}b=\frac{1}{{{\log }_{b}}a},\text{ }\left( b\ne 1 \right).\)

Логарифмирование: используется логарифм от правой и левой частей уравнения

Мини-максный: в том случае, когда \(\displaystyle a>1\) функция\( \displaystyle f(x)=lo{{g}_{a}}x\) представляет собой монотонно возрастающую, если \(\displaystyle 0<a<1\), то функция \(\displaystyle f(x)=lo{{g}_{a}}x\) имеет вид монотонно убывающей.

Последний способ решения логарифмических уравнений, то есть мини-максный, можно доказать, таким образом:

\(\displaystyle \left\{ \begin{array}{l}f\left( x \right)=g\left( x \right)\\f\left( x \right)\ge A\\g\left( x \right)\le A\end{array} \right.\Leftrightarrow \left\{ \begin{array}{l}f\left( x \right)=A\\g\left( x \right)=A\end{array} \right..\)

Решать логарифмические уравнения можно разными методами, включая разделение выражения по множителям, потенциирование и замену. Однако алгоритм основан на одном правиле. Смысл упрощения заключается в сведении логарифмического уравнения к упрощенному варианту. К примеру:

\(lo{{g}_{a}}\left( f\left( x \right) \right)~=~lo{{g}_{a}}\left( g\left( x \right) \right)\)

Далее можно продолжать решение без логарифмов:

\(f\left( x \right)=g\left( x \right).\)

Правило можно сформулировать следующим образом: в том случае, когда уравнение имеет с левой и правой стороны от знака «равно» логарифмы, обладающие одним основанием, данные логарифмы допустимо исключить и решать уравнение без них.

В этом правиле есть некоторое условие. Важно учитывать, что логарифм \(lo{{g}_{a}}\left( f\left( x \right) \right)\) определен только тогда, когда \(f\left( x \right)>0\)

После того, как найдены корни логарифмического уравнения, следует выполнить проверку.

Способ 1. Правило умножения на единицу разберемо с помощью примера:

\(lo{{g}_{2}}\left( 4-x \right)=7\)

Можно заметить, что в левой части есть логарифм, а в правой – он отсутствует. Необходимо выполнить преобразования уравнения, таким образом, чтобы в правой части тоже было выражение с логарифмом по основанию \(\displaystyle 2.\) При таком условии получится исключить логарифмы и существенно упростить решение. Следует умножить \( \displaystyle 7 \ на \ \displaystyle 1\). В результате:

\(\displaystyle 7\cdot 1\)

Но в этом случае логарифм не получен. Известно, что:

\(\displaystyle lo{{g}_{a}}a=1~(a>0,a\ne 1)\)

В данном случае требуется основание \displaystyle 2. Поэтому целесообразно взять \(\displaystyle a=2\). В таком случае получим:

\(\displaystyle 1=lo{{g}_{2}}2\)

\(\displaystyle 7=7\cdot 1=7\cdot ~lo{{g}_{2}}2\)

Далее необходимо выражение \displaystyle 7 занести в логарифм. Такая операция возможна, если воспользоваться правилом:

\(\displaystyle c\cdot lo{{g}_{a}}b=lo{{g}_{a}}{{b}^{c}}\)

Если применить данное правило к условиям задачи, получим:

\(\displaystyle 7\cdot ~lo{{g}_{2}}2=lo{{g}_{2}}{{2}^{7}}=lo{{g}_{2}}128\)

В этом случае исходное логарифмическое уравнение примет следующий вид:

\(\displaystyle lo{{g}_{2}}\left( 4-x \right)=lo{{g}_{2}}128\)

Далее можно исключить логарифмы и получить упрощенное уравнение:

\(\displaystyle 4-x=128\)

\(\displaystyle x=-124\)

В заключении необходимо выполнить проверку:

\(\displaystyle lo{{g}_{2}}\left( 4-\left( -124 \right) \right)=7\)

\(\displaystyle lo{{g}_{2}}128=7,~\)

Исходя из того, что \(\displaystyle {{2}^{7}}=128\), последнее уравнение будет справедливым, а \(\displaystyle x=-124\) является корнем.

Ответ: \(\displaystyle -124\)

Способ 2. Правило «превращения единицы» можно рассмотреть на примере вычисления данного уравнения:

\(lo{{g}_{5}}\left( 7-x \right)=\text{ }\!\!~\!\!\text{ }lo{{g}_{5}}\left( 3-x \right)+1\)

В данном случае целесообразно применить правило с названием «превращение единицы». Такая закономерность работает следующим образом:

\(1=lo{{g}_{5}}5\)

Преобразованное исходное логарифмическое уравнение в виде многочлена можно записать следующим образом:

\(lo{{g}_{5}}\left( 7-x \right)=\text{ }\!\!~\!\!\text{ }lo{{g}_{5}}\left( 3-x \right)+lo{{g}_{5}}5\)

Можно отметить, что одна часть уравнения содержит сумму или разность логарифмов, которые обладают одним основанием. Тогда применима формула, рассмотренная ранее:

\(lo{{g}_{a}}b+lo{{g}_{a}}c=lo{{g}_{a}}\left( bc \right)\)

Если использовать данную закономерность в решении задачи, то начальное уравнение можно для сравнения записать в таком виде:

\(lo{{g}_{5}}\left( 7-x \right)=\text{ }\!\!~\!\!\text{ }lo{{g}_{5}}5\left( 3-x \right)\)

Получим, что в левой и правой частях уравнения есть логарифмы. Далее их можно исключить и записать линейное уравнение:

\(7-x=5\left( 3-x \right)\)

\(7-x=15-5x\)

\(4x=8\)

\(x=2\)

В конце требуется проверка:

\(lo{{g}_{5}}\left( 7-2 \right)=lo{{g}_{5}}\left( 3-2 \right)+1\)

\(lo{{g}_{5}}5=lo{{g}_{5}}1+1\)

\(1=0+1\)

\(1=1\)

Правильность решения доказана.

Следует учитывать, что наличие ноля в правой части выражения объясняется следующим равенством:

\(lo{{g}_{a}}1=0,~a>0,a\ne 1\)

Ответ: 2

Способ 3. Использование свойств логарифма рассмотрим на примере задачи:

\(lo{{g}_{8}}{{2}^{8{x} -4}}=4\)

В данном случае есть два варианта решения:

• воспользоваться правилом умножения на единицу;
• использовать свойства логарифма.

Второй вариант:

\(c\cdot lo{{g}_{a}}b=lo{{g}_{a}}{{b}^{c}}\)

Считать следует, начиная с правой стороны:

\(lo{{g}_{8}}{{2}^{8{x} -4}}=\left( 8{x} -4 \right)lo{{g}_{8}}2\)

Далее необходимо разобраться с числом:

\(lo{{g}_{8}}2\)

В данном случае потребуется применить свойство:

\(lo{{g}_{{{a}^{c}}}}b=\frac{1}{c}lo{{g}_{a}}b\)

Исходя из того, что:

\(\displaystyle 8={{2}^{3}}\)

Получим:

\(\displaystyle lo{{g}_{8}}2=lo{{g}_{{{2}^{3}}}}2=\frac{1}{3}lo{{g}_{2}}2=\frac{1}{3}\cdot 1=\frac{1}{3}\)

В таком случае левая часть примет вид:

\(\displaystyle \frac{1}{3}\cdot \left( 8{x} -4 \right)=4\)

\(\displaystyle 8{x} -4=12\)

\(\displaystyle 8x=16\)

\(\displaystyle x=2\)

Далее необходимо проверить полученный результат:

\(\displaystyle lo{{g}_{8}}{{2}^{8\cdot 2-4}}=4\)

\(\displaystyle lo{{g}_{8}}{{2}^{12}}=4\)

\(\displaystyle lo{{g}_{8}}{{2}^{3\cdot 4}}=4\)

\(\displaystyle lo{{g}_{8}}{{8}^{4}}=4\)

\(\displaystyle 4lo{{g}_{8}}8=4\)

\(\displaystyle 4=4.\)

Ответ: 2

Существует ряд обязательных формул, которые необходимы для решения логарифмических уравнений:

• \(lo{{g}_{{{a}^{c}}}}b=\frac{1}{c}lo{{g}_{a}}b\)
• \(c\cdot lo{{g}_{a}}b=lo{{g}_{a}}{{b}^{c}}\)
• \(lo{{g}_{a}}b+lo{{g}_{a}}c=lo{{g}_{a}}\left( bc \right)\)
• \(lo{{g}_{a}}b-lo{{g}_{a}}c=lo{{g}_{a}}\left( \frac{b}{c} \right)\)
• \(lo{{g}_{a}}1=0,~a>0,a\ne 1\)
• \(lo{{g}_{a}}a=1~(a>0,a\ne 1)\)

Примеры деления и умножения

В задачах на логарифмы нередко встречаются уравнения с операциями умножения и деления. Правила работы с такими примерами можно записать в виде справедливых равенств:

\(loga(bc)=logab+logac(a>0,a≠1,b>0,c>0)\)

\(logabc=logab−logac(a>0,a≠1,b>0,c>0)\)

Выражение \(loga(f(x)g(x))\) будет определяться только в двух ситуациях:

• когда обе функции строго положительны;
• когда f(x) и g(x) обе меньше нуля.

Данное уравнение можно преобразовать и записать, как сумму: logaf(x)+logag(x), при условии, что \(f(x)>0 \ и \ g(x)>0\). Таким образом, ОДЗ сужается, что может привести к потере решений. Аналогично и со вторым уравнением для преобразования разности.

Решение:

Следует применить формулу суммы логарифмов и воспользоваться определением десятичного логарифма:

\(lg2 + lg50 = lg100 = 2\)

Ответ: 2

\(lg125/lg5\)

Решение:

С помощью формулы перехода к новому основанию запишем решение:

\(lg125/lg5 = log5125 = 3\)

Ответ: 3