Параллельные прямые: свойства и признаки

Что такое параллельные прямые

Основные признаки:

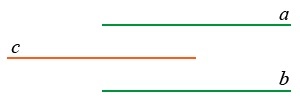
1. В случае, если две прямые параллельны третьей, они являются параллельными между собой. Так, если а || c и также b || c, то и a || b.
2. Если они перпендикулярны по отношению к третьей, то они не пересекаются: т.е., если а ⊥ с  и  b ⊥ c,  то  a || b.

Свойства параллельных прямых с доказательством

Они обладают следующими свойствами:

1. Через любую точку, которая, что немаловажно, не лежит на прямой, можно провести параллель, притом лишь одну. Данное утверждение является Евклидовой аксиомой. 
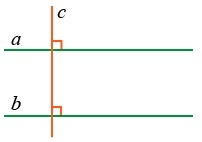
2. Если прямая, лежащая на плоскости, перпендикулярна одной из параллельных прямых, то она перпендикулярна и другой: если  a || b  и  c ⊥ a,  то  c ⊥ b.

Дано:  a || b  и  c ⊥ a

Доказать: c ⊥ b

Доказательство:

1. с пересекает а, следовательно, с пересекает также прямую, параллельную а, т.е. b.
2. Исходя из этого, можно утверждать, что с — это секущая по отношению к а и b.
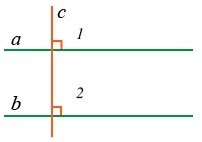
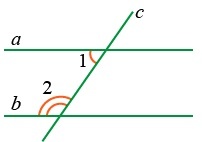
3. При секущей с ∠1 и ∠2 являются накрест лежащими.
4. Из свойств углов при параллельных прямых, пересеченных секущей, нам известно о равенстве накрест лежащих углов: следовательно, ∠1 = ∠2.
5. Как следствие, ∠2 = 90 градусов, что означает, что c ⊥ b. Что и требовалось доказать.

Признаки при пересечении секущей

Рассмотрим признаки, которые характерны для параллельных прямых при пересечении их секущей.

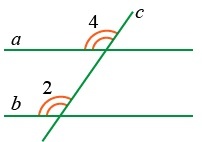
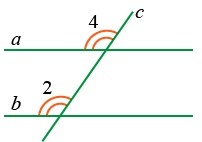
Если соответственные углы равны, то прямые не пересекаются. Если ∠2 = ∠4,  следовательно,  a || b.

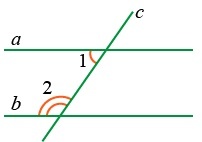
Если сумма внутренних односторонних углов равняется 180 градусам, то прямые являются параллельными. Если  ∠1 + ∠2 = 180°,  следовательно,  a || b.

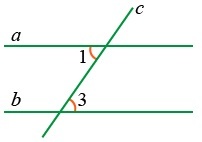
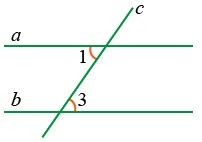
Если внутренние накрест лежащие углы равны, то прямые также являются параллельными. Если  ∠1 = ∠3,  следовательно,  a || b.

Свойства углов при параллельных прямых и секущей

Кроме того, следует охарактеризовать основные свойства углов, образованных при пересечении секущей прямой. Данные свойства являются обратными рассмотренным выше признакам.

При пересечении двух параллельных прямых третьей, сумма внутренних односторонних углов, образованных ими, равняется 180 градусам: если  a || b,  то  ∠1 + ∠2 = 180°.

В случае, когда две параллельные прямые пересечены третьей, соответственные углы, образованные ими, равны: если  a || b,  то  ∠2 = ∠4.

Если две параллельные прямые пересекаются третьей, накрест лежащие углы, образованные ими, равны: если  a || b,  то  ∠1 = ∠3.