Равнобедренный треугольник: определение, теорема о свойстве высоты
Что такое равнобедренный треугольник
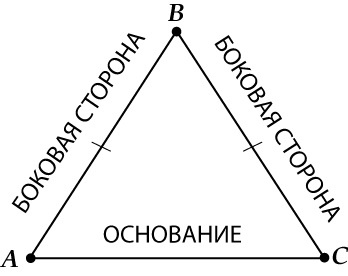
Равнобедренным называется тот треугольник, в котором две стороны равны.
Равные стороны называются боковыми, а третья – основанием.
Признаки равнобедренного треугольника
- треугольник является равнобедренным, если два его угла равны;
- треугольник, в котором высота и медиана, высота и биссектриса, биссектриса и медиана, проведенные к одной стороне, совпадают, является равнобедренным, а эта сторона – основанием.
Свойства равнобедренного треугольника
Свойство первое
В равнобедренном треугольнике углы при основании равны.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Доказательство теоремы:
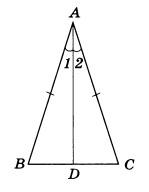
Дан равнобедренный ΔABC, в котором AB = AC. К его основанию проведена биссектриса AD.
Так как AD является биссектрисой, соответственно, угол ∠1 будет равен углу ∠2. Сторона AD – общая для ΔADB и ΔADC. Следовательно, они равны по первому признаку. Тогда верно утверждение, что угол ∠B равен углу ∠C.
Свойство второе
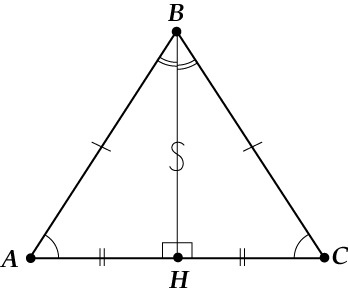
В равнобедренном треугольнике биссектриса, опущенная к основанию, является медианой и высотой.
Доказательство теоремы:
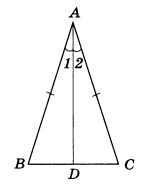
Дан равнобедренный ΔABC, в котором AB = AC. К его основанию проведена биссектриса AD.
Так как AD является биссектрисой, соответственно, угол ∠1 будет равен углу ∠2. Сторона AD – общая для ΔADB и ΔADC. Тогда эти треугольники равны по первому признаку. Тогда BD = DC. Следовательно, AD – медиана.
Сумма углов треугольника равна 180°, то есть ∠A + ∠B + ∠C = 180°. Так как AD – биссектриса, то угол ∠A = 2*∠1.
То есть
2*∠1 + 2*∠2 = 180°
∠1 + ∠2 = 90°
В ΔACD ∠CDA + ∠1 + ∠2 = 180°, следовательно, ∠CDA = 90°.
Тогда AD – высота.
Свойство третье
В равнобедренном треугольнике медианы (соответственно, высоты и биссектрисы), проведенные из вершин при основании, равны.
Доказательство теоремы:
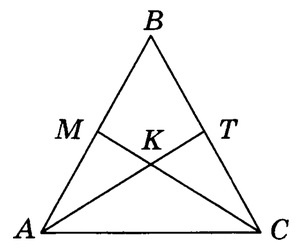
Дан равнобедренный ΔABC, в котором AB = AC.
∠BAT = ∠BCM, так как AT и MC – биссектрисы равных углов. ∠B – общий для ΔABT и ΔCBM. Следовательно, ΔABT и ΔCBM равны по второму признаку. Тогда AT = CM.
Формулы для равнобедренного треугольника
Формулы площади
\(S=\frac{1}{2}b\sqrt{\left(a+\frac{1}{2}b\right)\left(a-\frac{1}{2}b\right)}\)
\(S=\frac{1}{2}a^2\sin B\)
\(S=\frac{1}{2}ab\sin A\)
\(S=\frac{b^2}{4\tan\left(\frac{B}{2}\right)} \)
\(S=\frac{bh}{2} \)
\(S=\frac{b}{4}\sqrt{4a^2-b^2}\)
Формулы для нахождения стороны
\(a=\frac{b}{2\cos A}\)
\(b=a\sqrt{2\left(1-\cos B\right)}\)
\(b=2a\sin\left(\frac{B}{2}\right)\)
\(b=2a\cos A\)
Формулы для нахождения радиуса вписанной окружности
\(r=\frac{b}{2}\sqrt{\frac{2a-b}{2a+b}}\)
\(r=\frac{bh}{b+\sqrt{4h^2+b^2}}\)
\(r=\frac{h}{1+\frac{a}{\sqrt{a^2-h^2}}}\)
\(r=\frac{b}{2}\tan\left(\frac{A}{2}\right)\)
\(r=a\cos A\tan\left(\frac{A}{2}\right)\)
Пример решения задачи
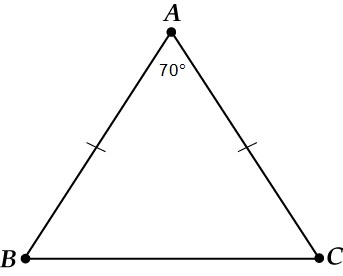
Дан равнобедренный ΔBAC, в котором угол ∠А = 70°. Найти угол ∠В.
Решение:
∠А + ∠В + ∠С = 180°.
Так как ΔBAC – равнобедренный, следовательно, ∠В = ∠С.
Тогда
∠А + 2*∠В = 180°, 70° + 2*∠В = 180°
2∠В = 180° - 70° = 110°
∠В = 55°
Ответ: ∠В = 55°
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так