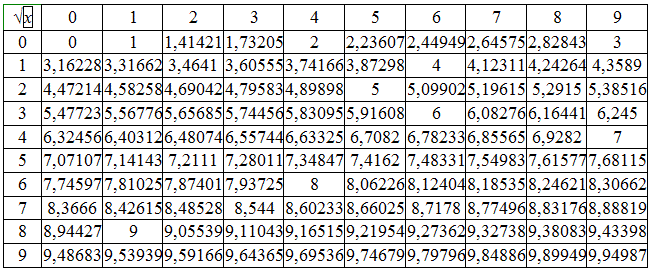
Таблица квадратных и кубических корней

Извлечение корней при помощи таблицы

Квадратные корни

\(t^2=a \)

Существуют способы вычислить корень неотрицательного числа вручную. Например, можно разложить число на квадратные множители и найти корни из них. Однако такое решение работает не для всех чисел, у большинства корень не будет натуральным числом. Для точного вычисления пользуются калькулятором или таблицей корней. 

С ее помощью можно найти корень любого числа от 0 до 99. В строках таблицы указываются десятки, в столбцах — единицы. Графа таблицы, где пересекаются нужные значения, и будет искомым числом. 

Кубические корни

\(t^3=a\)

В отличие от квадратного корня, в решении корней кубических ответ всегда один. Если исходное число положительное, то и корень будет положительным. Если кубический корень извлечен из отрицательного числа, то и он сам будет отрицательным.

Для нахождения кубических корней тоже есть таблицы. Они бывают разных масштабов, но чаще всего используют стандартную для чисел от 0 до 99. В ней также десятки расположены в строках, а единицы — в столбцах.

Помимо таблиц корней второй и третьей степени существуют таблицы для более высоких степеней, но обычно при вычислениях ими не пользуются.

Особенности использования для квадратных и кубических корней

Таблицы квадратных и кубических корней используются по одному принципу. Однако, так как одна степень — четная, а другая нет, существуют различия в том, как решать выражения с этими корнями.

Из определения арифметического квадратного корня следует, что подкоренное число не может быть отрицательным. Это ввели для того, чтобы сделать понятие корня однозначным. Однако есть более широкое понятие алгебраического квадратного корня.

При работе с таблицей стоит учитывать, какой именно квадратный корень нужно найти — арифметический или алгебраический.

В первом случае достаточно взять значение из таблицы корней без дополнительных действий.

В задаче с алгебраическим корнем ответ зависит от того, какое число стоит под корнем. Если подкоренное число больше нуля, то корня будет два — положительный и отрицательный. Если возведенное в степень число отрицательно, то задача не имеет решения. Вторая степень является четной, поэтому нет такого числа, которое в квадрате дало бы отрицательное значение. 

Кубический корень — степень нечетная, поэтому подкоренное значение может быть и отрицательным, и положительным. Такое же значение будет иметь и ответ. То есть к результату из таблицы нужно лишь добавить минус, если искомый корень возведен в число меньше нуля. 

Примеры с описанием

Поиск квадратных корней

В числе 84 количество десятков — 8, поэтому по таблице квадратов ищем строку, обозначенную слева цифрой 8. Нужное количеств единиц — 4, значит, нужен столбец с цифрой 4 наверху. Находим ячейку, где эти столбец и строка пересекаются. Там находится число 9.16515, оно и будет искомым ответом. Если требуется, его можно округлить до сотых (9.17) или десятых (9,2).

В таких случаях квадратный корень обычно принимается за алгебраический, поэтому смотрим на подкоренное число. Оно положительное, поэтому ответа будет два. Находим по таблице строку с количеством десятков, равным 1, и столбец, где число единиц — 7. В их пересечении находится ячейка с числом 4.12311. Для арифметического корня этого было бы достаточно, для алгебраического мы приводим два ответа: x=4.12311 и x=–4.12311. При необходимости округляем до сотых (4.12, –4.123) или десятых (4.1, –4.1). Оба этих числа при возведении в квадрат будут равны 17. 

Ищем по таблице ячейку, в которой пересекутся строка со значением 2 и столбец со значением 3. В ней указано число 4.79583. Однако обращаем внимание, что подкоренное число меньше нуля, поэтому найденный результат ответом не будет. В решении указываем:
\(\sqrt[{}]{-23}\neq4.79583\\\sqrt{-23}\neq-4.79583\)

Поиск кубических корней

В таблице кубических корней ищем строку с десятками, равными 5, и столбец, где значение единиц — 5. Они пересекаются в ячейке с числом 3.80295. Так как подкоренное число положительное, то и ответ будет с таким же знаком. Искомое значение x — 3.80295 (или 3.8).

Находим по таблице графу, где пересекаются строка с обозначением 4 и столбец с цифрой 8. В ней располагается число 3.63424. Смотрим на число, которое был возведено в куб, — оно отрицательное. Значит, и ответ будет с минусом. Таким образом, x=–3.63424.