Таблица квадратов натуральных чисел
Что такое таблица квадратов натуральных чисел
Квадрат чисела — это число, возведенное во вторую степень, то есть умноженное само на себя.
\(a^2=a\cdot a\)
Эта операция называется так, потому что аналогична вычислению площади квадрата.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
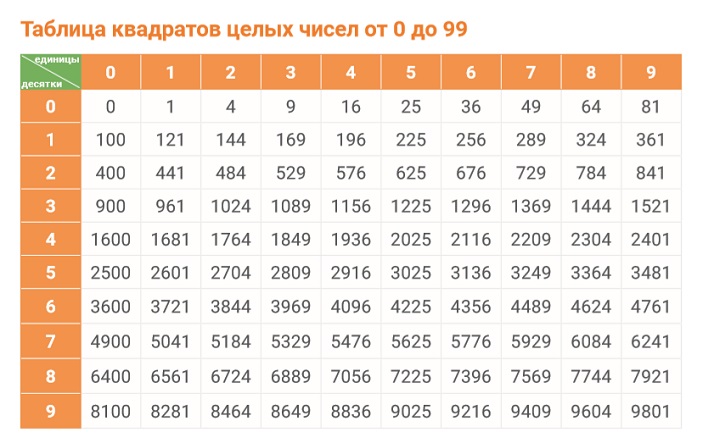
Таблица квадратов — это таблица, в которой содержатся квадраты чисел.
С помощью таблицы в алгебре решают квадратные уравнения: возводят числа в квадрат и вычисляют квадратный корень. В геометрии ей пользуются при решении задач с теоремой Пифагора или теоремой косинусов.
Как правило, в таблице по вертикали указаны десятки, а по горизонтали — единицы. На пересечении находится квадрат искомого числа.
Особенности использования для вычисления квадратов
Благодаря таблице можно выделить особенности квадрата целого числа.
- Последняя цифра квадрата может быть равна 0, 1, 4, 5, 6 или 9. Квадрат не оканчивается цифрами 2, 3, 7 и 8.
- Количество нулей на конце квадрата всегда четное.
- Квадрат натурального числа либо делится на 4, либо при делении на 8 дает остаток 1.
- Квадрат натурального числа либо делится на 9, либо при делении на 3 дает остаток 1.
Примеры возведения двухзначных и трехзначных чисел
Рассмотрим пример вычисления квадрата двузначного числа по таблице.
Задача 1
Вычислить \(38^2\).
Решение
Можно умножить число 38 на себя, а можно воспользоваться таблицей и сразу записать значение.
Ответ: \(38^2\;=\;1444\)
Рассмотрим пример решения геометрической задачи по теореме Пифагора.
Задача 2
Один из катетов прямоугольного треугольника равен 12. Другой катет равен 9. Найти гипотенузу.
Решение
Согласно теореме Пифагора, квадрат гипотенузы равен сумме квадратов катетов. Исходя из таблицы, \(12^2=144\), а \(9^2=81\). Сумма квадратов катетов равна 225. Исходя из таблицы, \(\sqrt{225}=15\).
Ответ: гипотенуза равна 15.
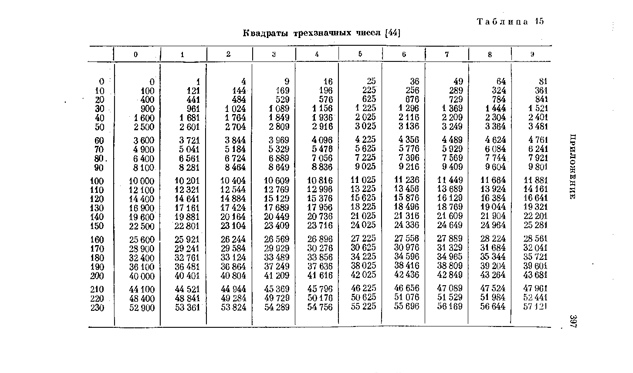
Существуют и расширенные таблицы, в том числе — для вычисления квадратов трехзначных чисел.
Задача 3
Вычислить квадрат числа 123.
Решение
Можно умножить число 123 на себя, а можно воспользоваться таблицей и сразу записать значение. Необходимо найти пересечение ряда 120 и столбца 3.
Ответ: 15129.
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так