Таблица косинусов
Что такое таблица косинусов
В таблице косинусов содержатся посчитанные значения косинусов углов.
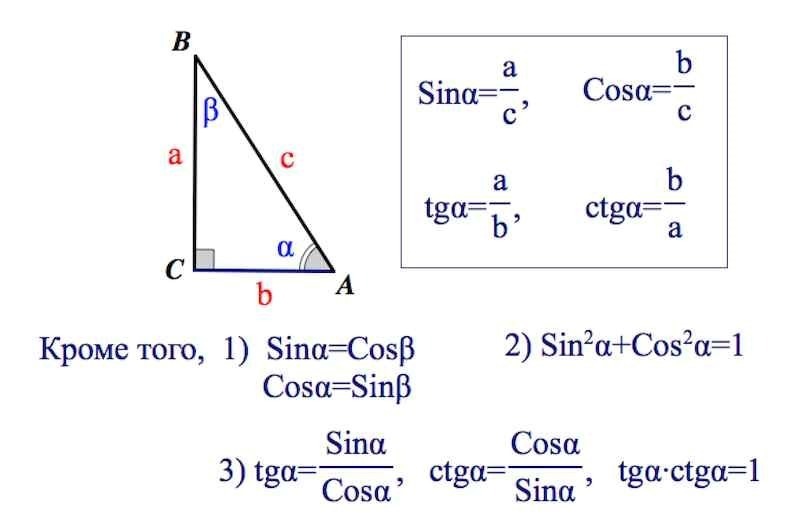
Косинус в тригонометрии (cosα) — это отношение прилежащего катета к гипотенузе. Важно помнить, что его значение может варьироваться от -1 до 1.
Таблица позволит узнать значение косинуса от любого угла без применения инженерного калькулятора.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Варианты таблиц
Есть несколько вариантов подобных таблиц.
Таблица косинусов углов в радианах и градусах
Радиан — это величина центрального угла, который опирается на дугу, равную радиусу окружности.
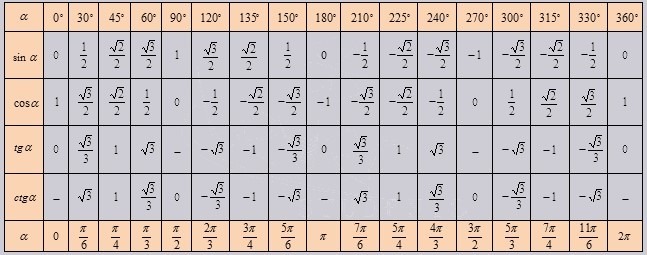
Также есть расширенный вариант таблицы, основанный на свойстве периодичности.
Периодическая функция повторяет свои значения через некоторый регулярный интервал аргумента.
Для косинусов и тангенсов углов значения функции повторяются с отрицательным знаком через каждые 180°. То есть если при 0° косинус угла равен 1, то при 180° он будет равен -1.
Таблица Бардиса
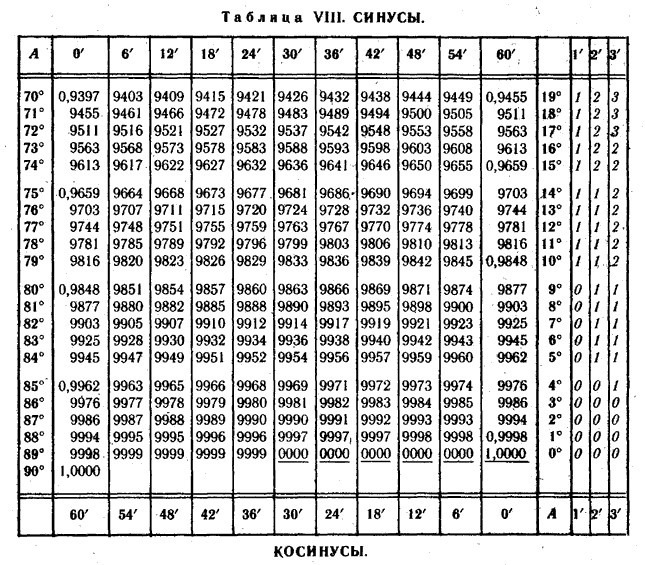
Она позволяет определить косинус угла с точностью до 4 знаков после запятой. В ней содержатся значения углов в градусах и минутах.
Для косинуса: значение угла в градусах находятся в таблице справа, в минутах — снизу.
Для синуса, наоборот, градусы — слева, минуты — сверху.
Например, косинус угла в 10°12', нужно искать на пересечении значения в 10° (4 справа столбик под обозначением «А») и 12' (самая нижняя строка таблицы). Косинус равен 0,9842.
В таблице представлены только углы, кратные шести минутам. Поэтому если нужного значения нет в таблице, надо работать с поправками в 1,2,3 минуты.
Необходимо найти косинус угла, равного 15°7'.
В таблице находим косинус угла 15°6': он равен 0,9655. И прибавляем необходимую поправку в 1'.
\(\cos15^\circ7'\;=\;0,9655\;+\;0,0001\;=\;0,9656\)
Как легко запомнить таблицу
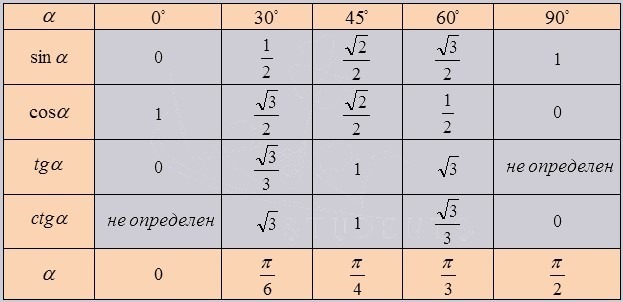
Рассмотрим вариант запоминания обычной таблицы синусов и косинусов в радианах и градусах.
Важно запомнить соответствия значений углов в радианах и градусах:
- 0 радиан = 0°.
- П/6 = 30°.
- П/4 = 45°.
- П/3 = 60°.
- П/2 = 90°.
Чтобы легче запомнить, вместо П можно подставлять 180°.
В строке таблицы с заголовком sin нужно записать числа от 0 до 4 по порядку и извлечь из них корень, а затем разделить на 2.
Если не извлекаются полные числа, то нужно оставить как есть. Например, sin 45° = √2/2. Это значение останется неизменным.
Получаются следующие значения:
0, 1/2, √2/2, √3/2, 1.
Значения косинусов такие же, только в обратном порядке:
1, √3/2, √2/2,1/2, 0.
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так