Таблица синусов Брадиса

Как пользоваться таблицей Брадиса

Математик Владимир Модестович Брадис в начале ХХ века изобрел метод, значительно упрощающий и сокращающий громоздкие вычисления. Инновационный подход облегчил работу инженерным специалистам и стал наиболее эффективным решением до разработки калькуляторов.

В сборнике представлено 19 табличных форм, в том числе, математические инструменты для вычисления синусов углов. Пособия обладают идентичной структурой для каждой из тригонометрических функций. В процессе определения искомой величины следует найти значение, записанное в клетку, которая лежит на пересечении колонки и строки, задающих характеристику аргументу. С помощью функциональных массивов данных допустимо вычислять две пары значащих цифр какой-либо функции.

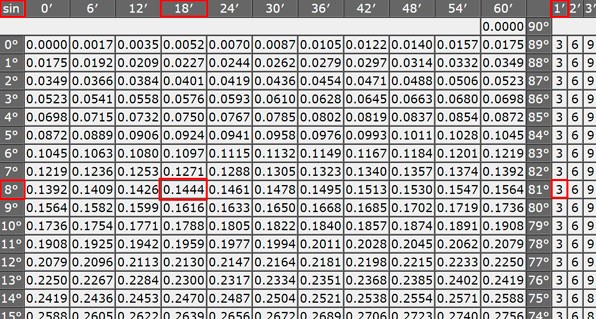
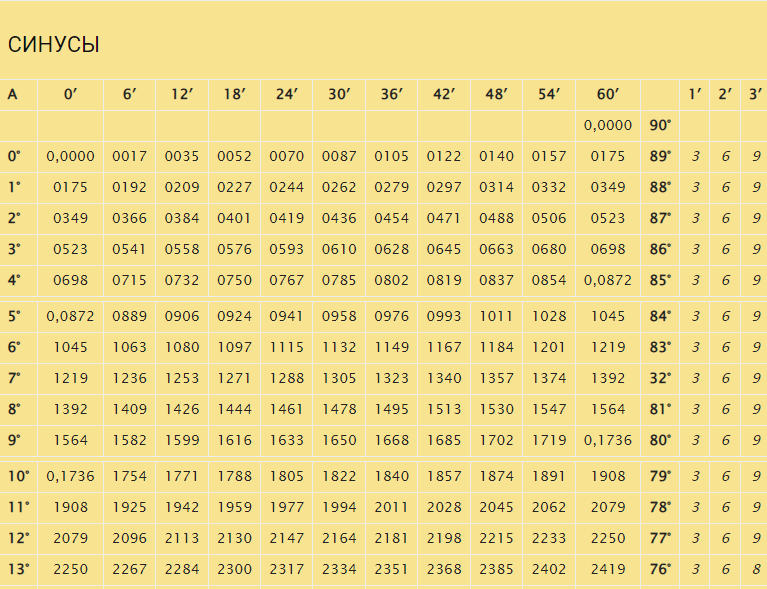
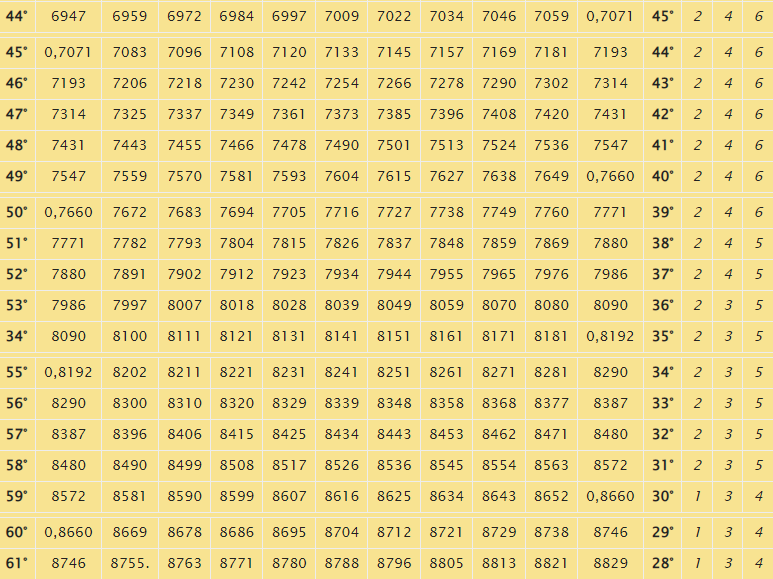
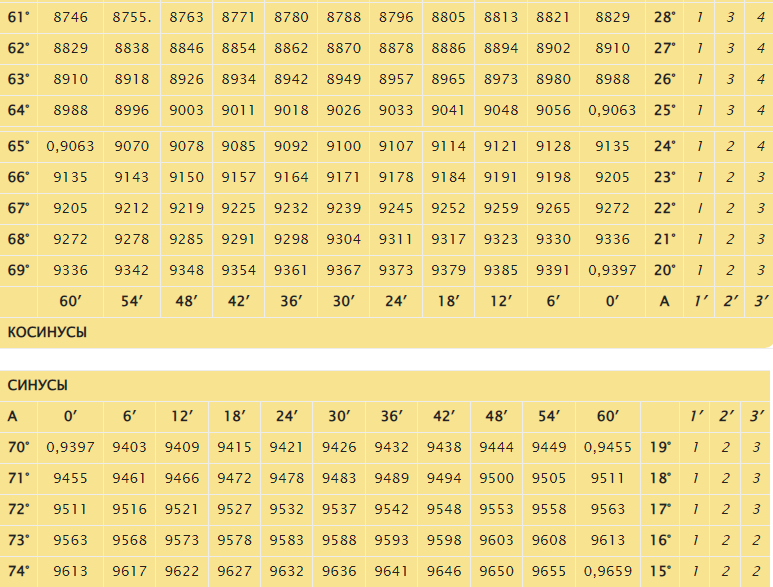
В таблице перечислены величины углов, которые кратны 6 минутам. При разборе задач по тригонометрии нередко возникают сложности, связанные с отсутствием нужного угла. Простым решением подобных примеров служит выбор максимально близкого значения и последующего суммирования или вычитания из найденного числа разницы в минутах. По стандартной схеме синус определяют в соответствии с градусной мерой угла:

• градусы записаны в колонке с левой стороны;
• сверху строкой перечислены минуты.

Представим, что по заданию необходимо вычислить синус угла, равного 8°19′. Ознакомившись с табличной формой, можно сделать вывод об отсутствии заданного значения. По этой причине следует ориентироваться на близлежащие величины, то есть для конкретного случая подходит 8°18′. Исходя из табличных сведений, получим:

sin(8°18′)=0,1444

На следующем этапе вычислений нужно применить поправочные значения. Заметим, что разница между sin(8°18′) и sin(8°19′) равна одной минуте(1′) по направлению к увеличению. Таким образом, целесообразно использовать в дальнейших расчетах значение в 1 минуту, соответствующее числу 3. Перед записью окончательного ответа к 0.1444 прибавим 0,0003. В результате sin(8°19′) равен 0,1447.

Источник: urokmatematiki.ru

Таблица синусов углов от 0° до 180°

В настоящее время таблицы с итогами озвученных расчетов не утратили актуальность. Пособия, обладающие прикладной ценностью, отправлены в печать еще в советское время. Массивы данных публиковали в формате компактных брошюр. Справочные материалы незаменимы при работе с примерами, содержащими комбинированные и нетривиальные функции, удобны и эффективны в использовании.

Источник: tablici.info

Таблица синусов углов от 181° до 360°

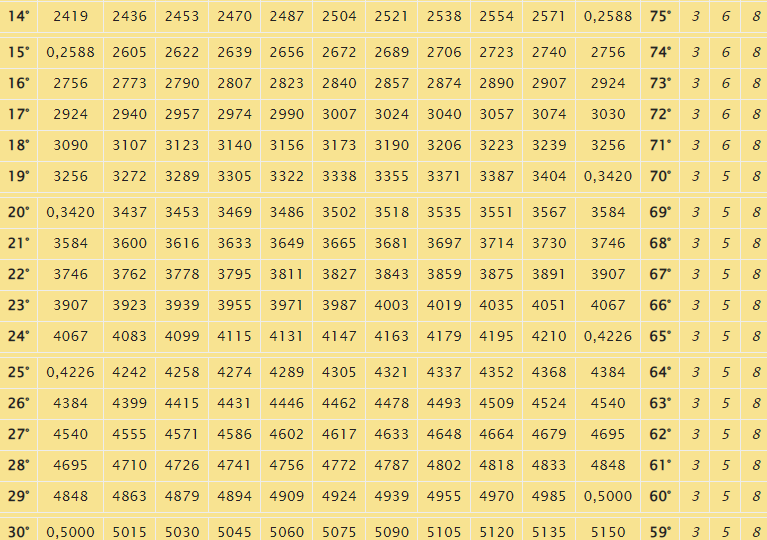
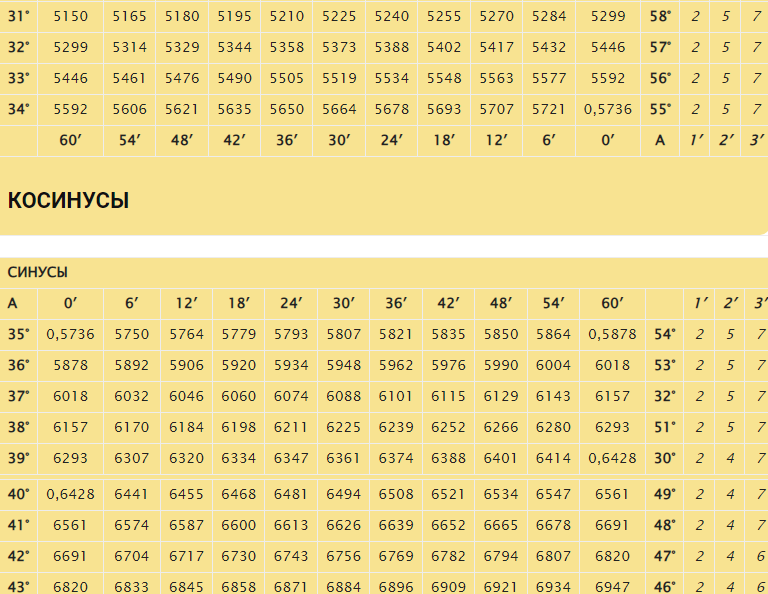
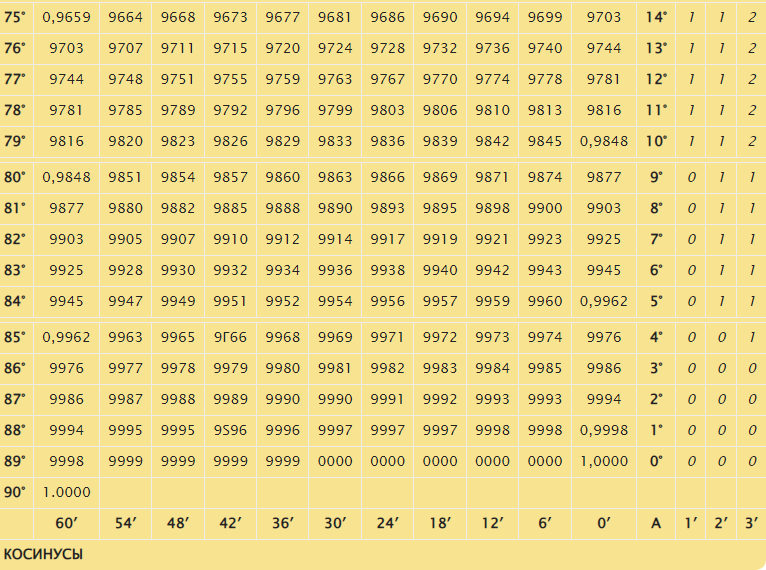
При известном синусе для какого-либо острого угла несложно вычислить значение для прочих углов. В табличной форме предусмотрены величины синусов применительно для каждого интервала:

1. менее 90°;
2. 91°-180°;
3. 181°-270°;
4. 271°-З60°.

Когда по условиям задания требуется определить, чему равен синус угла, соответствующего интервалу 91°-180°, из величины развернутого угла вычитают заданный угол, чтобы рассчитать синус. Решим в качестве наглядной задачи следующий пример:

sin(179°)=sin(180°-179°)=sin(1°)=0,0175

Существует еще один полезный способ решения тригонометрических заданий с помощью таблицы Брадиса. Данный метод состоит в поиске величины угла, равного значению из интервала 181°-270°. В процессе решения нужно от 181° отнять известный угол и определить синус со знаком минуса. Подобный принцип удобно проанализировать на таком примере:

sin(181°)=sin(180°-181°)=sin(-1°)=-sin(1°)=-0,0175

Вычисление угла из интервала от 271° до З60° включает в себя действия по вычитанию величины в З60° из заданного по условию задачи угла и расчете синуса, значение которого принадлежит множеству отрицательных чисел. Продемонстрируем на практике особенности вычислений:

sin(З59°)=sin(З59°-З60°)=sin(-1°)=-sin(1°)=-0,0175.

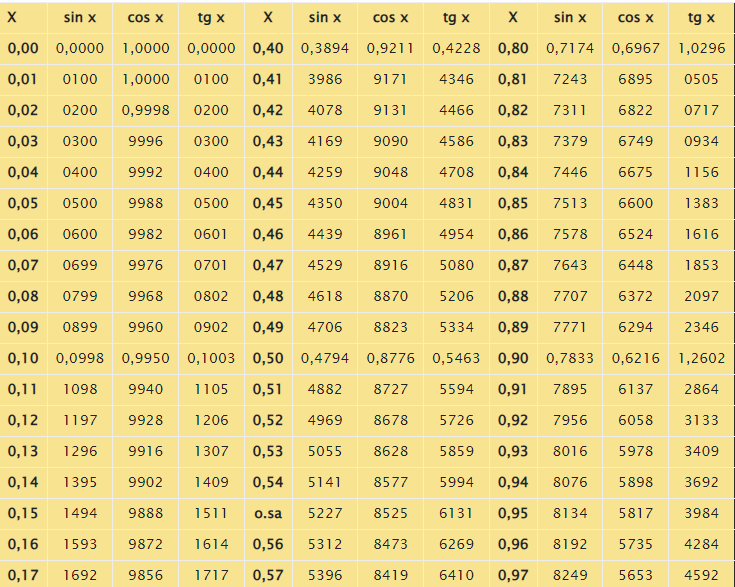
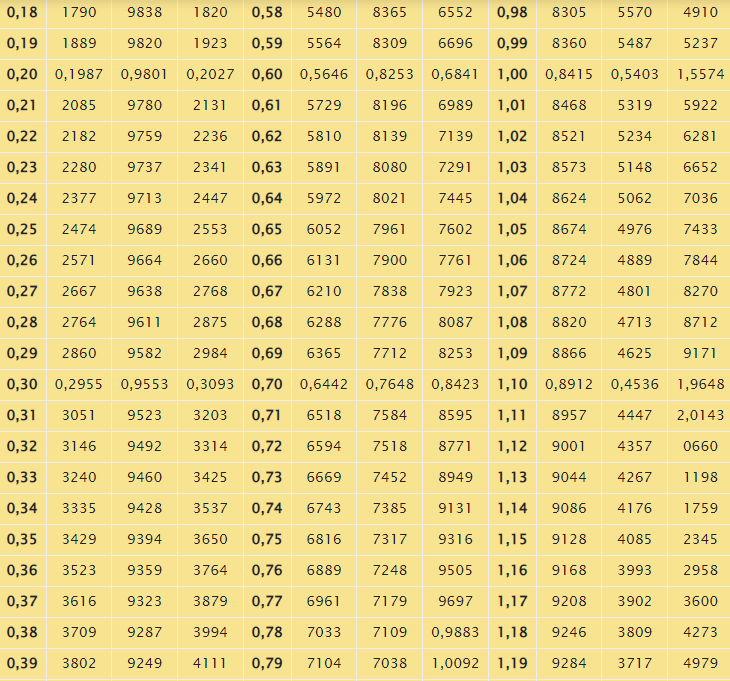
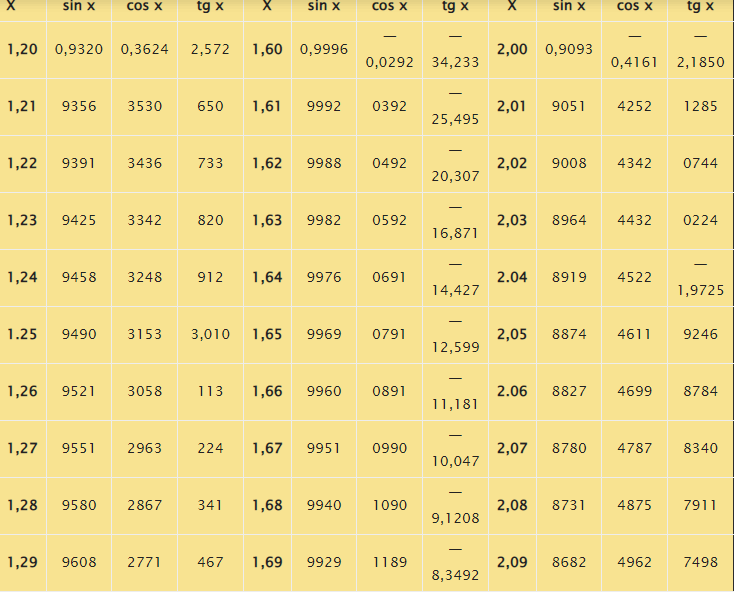
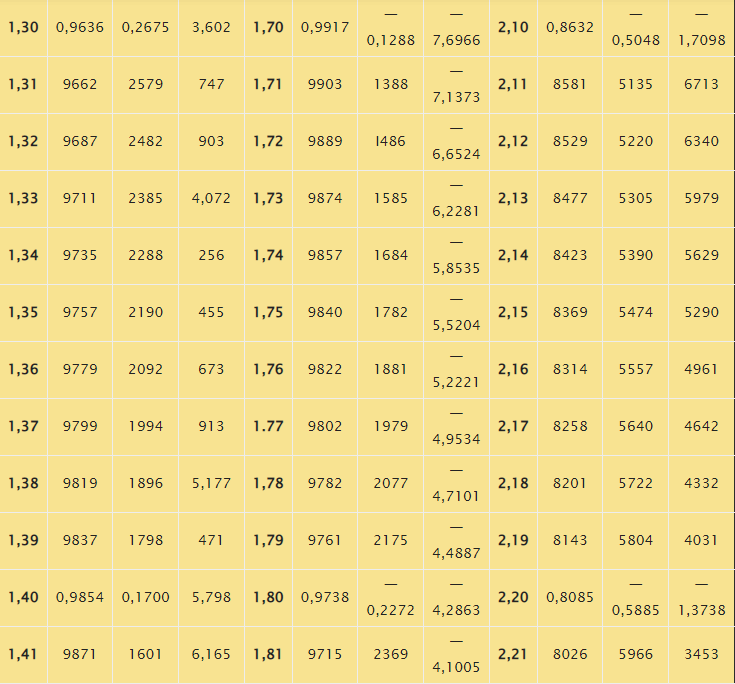
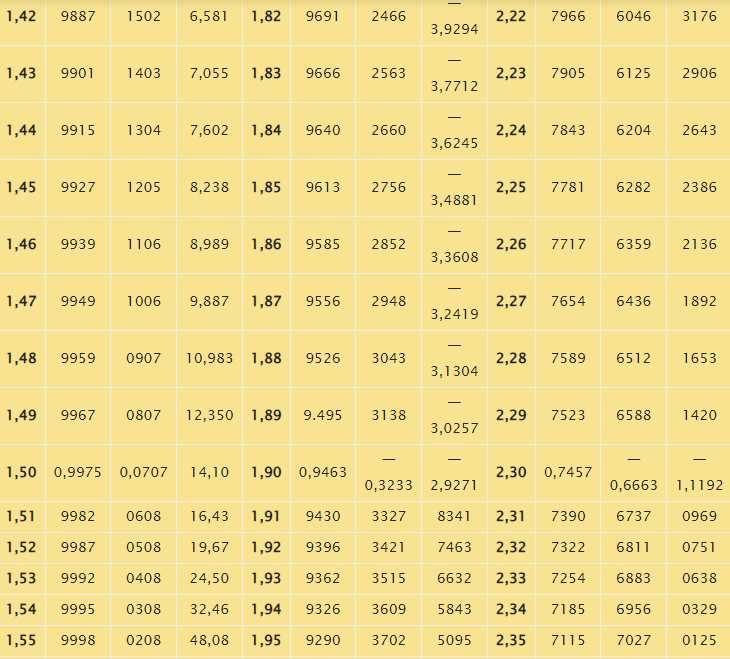
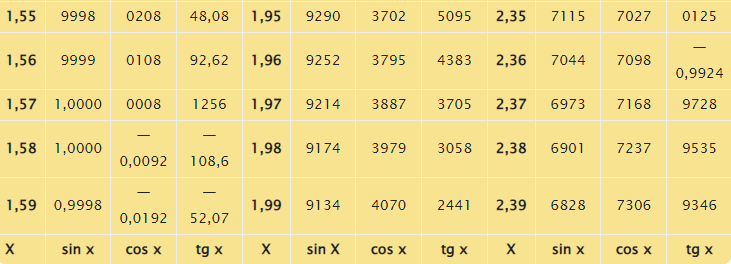
Таблица синусов в радианах

Заметим, что с целью записи аргументов в табличных формах Брадиса использованы градусные меры углов. В случае необходимости перевода таких величин в радианы необходимо выполнить умножение на 180 и деление полученного результата на число, равное З,1415926. Справочник содержит соответствующую таблицу, представленную ниже.

 

Источник: tablici.info