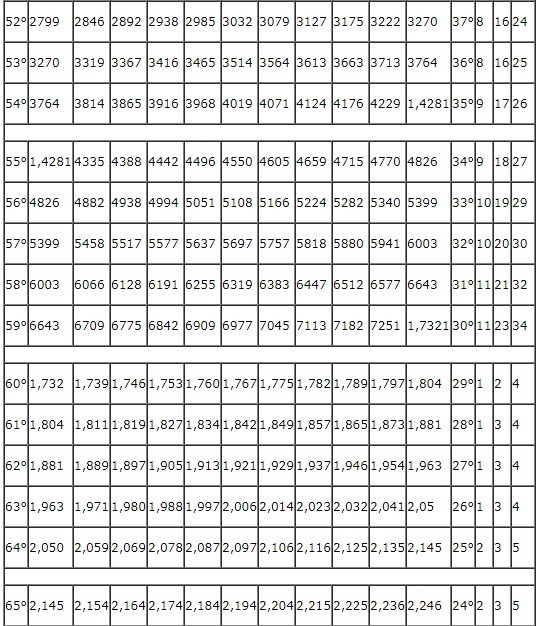
Тригонометрическая таблица Брадиса для тангенса и котангенса

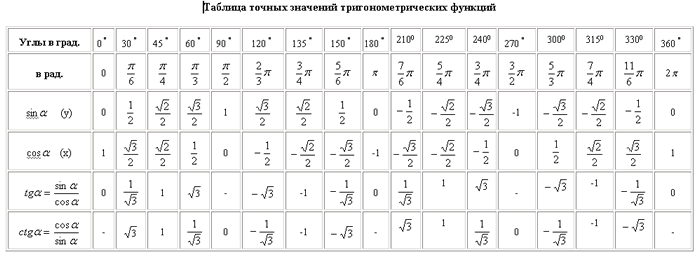
Таблица основных тригонометрических функций для углов 0, 30, 45, 60, 90, ..., 360 градусов

По определению, которому соответствует синус, косинус, тангенс и котангенс, достаточно просто рассчитать данные функции для углов 0 и 90 градусов. Значения будут записаны таким образом:

sin 0=0; cos 0=1; tg 0=0; tg 0=0; ctg 0 не обозначен;

sin 90°=1; cos 90°=0; сtg 90°=0; tg 90° не обозначен.

Величины синусов, косинусов, тангенсов и котангенсов в науке геометрии рассчитывают, как соотношения сторон, которыми обладает прямоугольный треугольник с углами в 30, 60 и 90 градусов, а также 45, 45 и 90 градусов.

Тригонометрические функции, если угол острый в прямоугольном треугольнике, определяют таким образом:

• синусом является отношение противоположного катета и гипотенузы;
• тангенс рассчитывают с помощью отношения противоположного катета к прилегающему;
• косинус представляет собой отношение прилегающего катета к гипотенузе;
• котангенс в виде отношения прилегающего катета к противоположному.

Исходя из определений, можно записать вычисления функций, включая дроби и корни. Одной из значимых характеристик, которыми обладают функции в тригонометрии, является периодичность. Данное свойство позволяет существенно увеличить число вариаций формул приведения. Точные малые значения представлены в таблице:

Применять таблицу для решения задач достаточно просто. Принцип работы с данными интуитивно понятен. Место, где пересекаются строка и столбец, указывает на полное значение функции для определенного угла.

Таблица Брадиса для тангенса и котангенса

Владимир Модестович Брадис  (1890 – 1975) был советским математиком-педагогом, а с 1954 года являлся членом-корреспондентом АПН СССР. Брадис разработал таблицы четырехзначных логарифмов и натуральных тригонометрических величин, которые были опубликованы впервые в 1921 году.

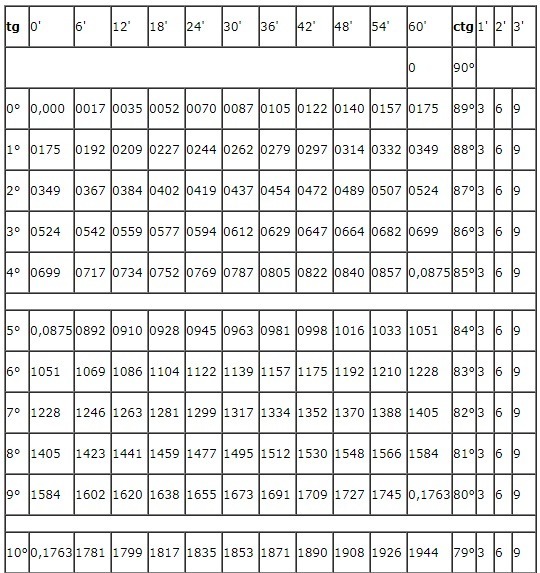
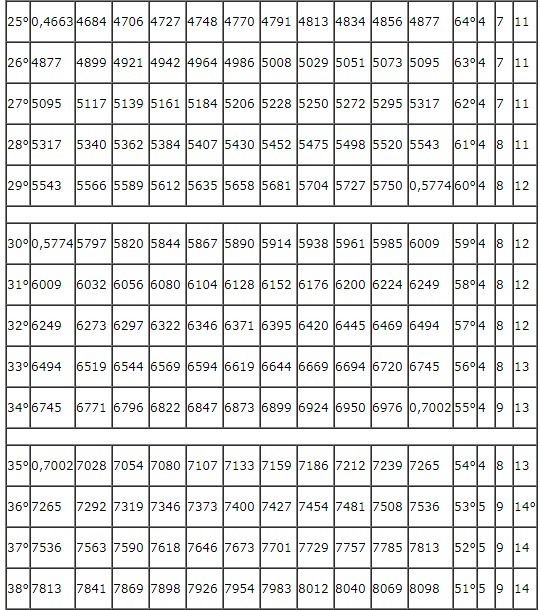
Таблица состоит из двух частей. Первая структура содержит тангенсы от 0 до 75 градусов и котангенсы от 15 до 90 градусов. Они определены по средствам специальных столбцов для 1, 2 и 3 минут. Вторая часть включает тангенсы от 75 до 90 градусов и котангенсы от 0 до 15 градусов, точность записи которых соответствует 1 минуте угла. Таблица Брадиса:

 

 

Как пользоваться таблицами Брадиса

Определить тангенс и котангенс угла с помощью табличных данных достаточно просто. Рассмотрим конкретный пример:

$$tg\;10^\circ\;=\;0,1763$$

Используя специальные колонки, можно определить:

\(tg\;10^\circ\;12'\;=\;0,1799,\;tg\;10^\circ\;24'\;=\;0,1835\)

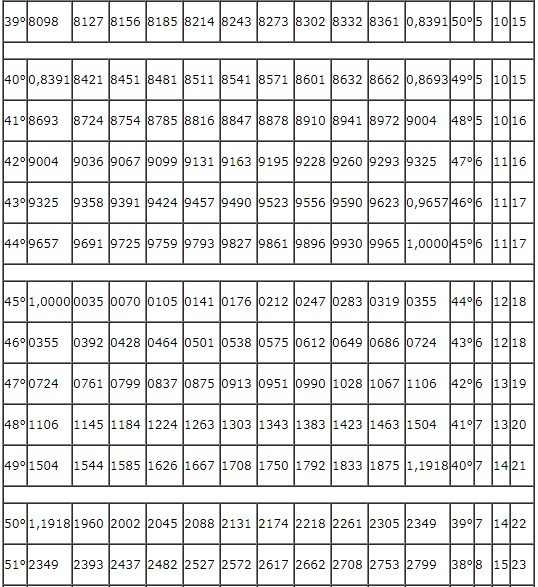
\(tg\;50^\circ\;=\;1,1918\)

С помощью дополнительной колонки можно определить, что:

\(tg\;50^\circ\;12'\;=\;1,2002,\;tg\;50^\circ\;24'\;=\;1,2088\)

Получить более точные показатели достаточно просто, необходимо применить поправочные коэффициенты.

\(tg\;10^\circ\;15'\;=\;tg\;10^\circ\;12'\;+\;0,0009\;=\;0,1799\;+\;0,0009\;=\;0,1808\)

\(tg\;50^\circ\;22'\;=\;tg\;50^\circ\;24' -0,0014\;=\;1,7705-0,0004\;=\;0,7701\)

В правом столбце таблицы Брадиса, где указаны тангенсы, можно определить котангенс. В качестве альтернативы можно вычислить его с помощью тангенса угла, который дополняет искомый до 90°:

\(ctg\;10^\circ\;=\;tg\;80^\circ\;=\;5,671\)

Благодаря дополнительным столбцам можно определить:

\(сtg\;10^\circ\;12'\;=\;5,558,\;сtg\;10^\circ\;24'\;=\;5,449\)

Таким же образом можно получить результат, если посмотреть тангенс дополняющих углов: 79° 48' и 79° 36' соответственно.

\(ctg\;50^\circ\;=\;0,8391\)

В дополнительной колонке можно увидеть, что:

\(ctg\;50^\circ\;12'\;=\;0,8332,\;ctg\;50^\circ\;24'\;=\;0,8273\)

Другой способ — узнать тангенс дополняющих углов 39° 48' и 39° 36'.

Особенность таблицы заключается в том, что тангенсы и котангенсы записаны в двух таблицах:

• тангенсы углов от 0° до 76° (и котангенсы от 90° до 24°);
• тангенсы от 76° до 90° (и котангенсы от 24° до 0°).

• \(tg\;80^\circ\;(\;ctg\;10^\circ)\;=\;5,671\)
• \(tg\;80^\circ\;1'\;(\;ctg\;10^\circ\;59')\;=\;5,681\)
• \(tg\;80^\circ\;2'\;(\;ctg\;10^\circ\;58')\;=\;5,\;691\)
• и далее таким же образом.

Тангенс и котангенс можно вычислить с помощью таблицы Брадиса с синусами и косинусами. Для этого предусмотрены специальные уравнения:

• \(tg\;\alpha\;=\;\sin\;\alpha\;/\;\cos\;\alpha\)
• \(ctg\;\alpha\;=\;\cos\;\alpha\;/\;\sin\;\alpha\)

После того, как нужные значения подставлены в формулы, получим результат:

• \(tg\;10^\circ\;=\;0,1736\;/\;0,9848\;=\;0,1763\)
• \(ctg\;50^\circ\;=\;0,6428\;/\;0,7660\;=\;8391\)