Все о таблице Брадиса: синусы, косинусы, тангенсы, котангенсы

Что такое таблица Брадиса 

Использование калькуляторов при сложных расчетах (например, формулах с применением логарифмов) сегодня считается стандартом по умолчанию. Но еще 20-30 лет назад, когда вычислительная техника была распространена не так сильно, на помощь приходили другие способы вычислений — с помощью специальных таблиц, логарифмической линейки или арифмометра.

Свое название они получили от брошюры «Четырехзначные математические таблицы», составленной Владимиром Брадисом. Книга неоднократно переиздавалась в советское время большими тиражами (до 500 000 экземпляров) и широко использовалась в учебном процессе — на уроках алгебры, геометрии и физики.

Функциональные возможности таблицы

Самыми распространенными являются таблицы, содержащие тригонометрические функции (например, синус, косинус, тангенс, котангенс и арктангенс).

В целом, в сборнике Брадиса содержалось более 20 таблиц, в том числе, помогавшие найти значения:

• значение дробей вида 1/n;
• квадратов;
• квадратных корней;
• площади круга определенного диаметра;
• радианной меры;
• мантиссы десятичных логарифмов;
• номограммы для решения отдельных уравнений.

Таблица синусов и косинусов

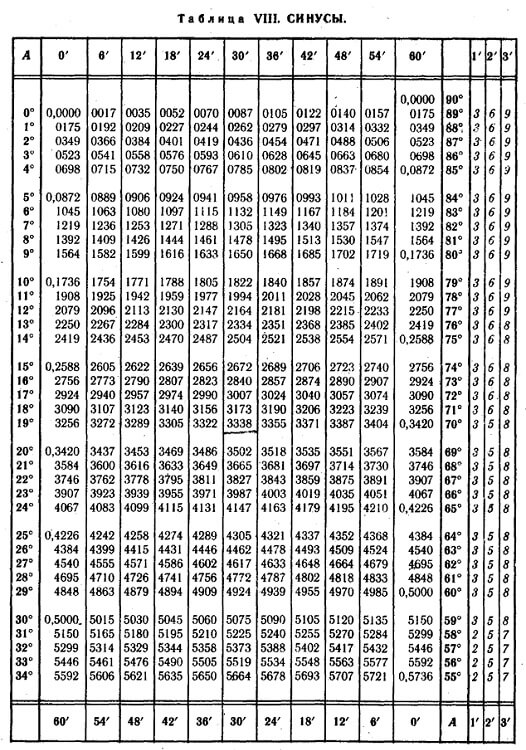
В силу широкого использования синусов и косинусов в учебных задачах, это самая распространенная из таблиц Брадиса. Она дает значение этих тригонометрических функций для любого острого угла от 0° до 90°. С помощью дополнительных колонок можно находить и более точные спецификации. Это 6', 12',18, 24', 30', 36', 42', 48' и 54' для углов указанного диапазона, например:

• \(\sin\;10^\circ\;=\;0,1736\). С помощью дополнительных колонок находим — \(\sin\;10^\circ\;12'\;=\;0,1771,\;\sin\;10^\circ\;24'\;=\;0,1805\);
• \(\sin\;50^\circ\;=\;0,7660\). Обращаясь к дополнительной колонке выясняем, что \(\sin\;50^\circ\;12'\;=\;0,7683,\;\sin\;50^\circ\;24'\;=\;0,7705\).

Если нужны еще более точные показатели, то нужно использовать поправочные коэффициенты, отнимая и прибавляя их к ближайшему табличному значению минут. Используя их, находим:

• \(\sin\;10^\circ\;15'\;=\;\sin\;10^\circ\;12'\;+\;0,0009\;=\;0,1771+0,0009\;=\;0,1780\);
• \(\sin\;50^\circ\;22'\;=\;\sin\;50^\circ\;24'-0,0004\;=\;0,7705-0,0004\;=\;0,7701\).

Для нахождения косинусов можно использовать значения в правой колонке, но куда удобнее вычислять через синус угла, дополняющего до 90°. В этом случае:

• \(\cos\;10^\circ\;=\;\sin\;80^\circ\;=\;0,9848;\)
• \(\cos\;50^\circ\;=\;\sin\;40^\circ\;=\;0,6428.\)

Аналогично проводят и более точные вычисления, в том числе — с использованием поправочных коэффициентов:

• \(\cos\;10^\circ\;12'\;=\;\sin\;79^\circ\;48'\;=\;0,9842;\)
• \(\cos\;10^\circ\;15'\;=\;\sin\;79^\circ\;45'\;=\;\sin\;79^\circ\;48'-0,0002\;=\;0,9842-0,002\;=\;0,9840;\)
• \(\cos\;50^\circ\;24'\;=\;\sin\;39^\circ\;36'\;=\;0,6374;\)
• \(\cos\;50^\circ\;22'\;=\;\sin\;39^\circ\;38'\;=\;\sin\;39^\circ\;36'\;+\;0,0004\;=0,6374\;+\;0,0004\;=\;0,6380.\)

 Таблица для тангенсов и котангенсов

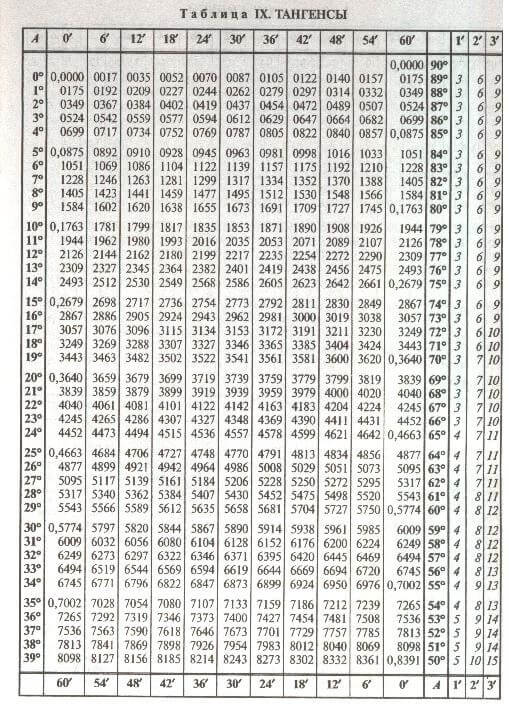
Аналогичным образом с помощью соответствующей таблицы Брадиса можно найти значения тангенса:

• \(tg\;10^\circ\;=\;0,1763\). Прибегая к помощи дополнительных колонок находим — \(tg\;10^\circ\;12'\;=\;0,1799,\;tg\;10^\circ\;24'\;=\;0,1835\);
• \(tg\;50^\circ\;=\;1,1918\). Заглянув в дополнительную колонку выясняем, что \(tg\;50^\circ\;12'\;=\;1,2002,\;tg\;50^\circ\;24'\;=\;1,2088\).

Для более точных показателей применяем поправочные коэффициенты (аналогично, как для таблиц синуса и косинуса):

• \(tg\;10^\circ\;15'\;=\;tg\;10^\circ\;12'\;+\;0,0009\;=\;0,1799\;+\;0,0009\;=\;0,1808\);
• \(tg\;50^\circ\;22'\;=\;tg\;50^\circ\;24' -0,0014\;=\;1,7705-0,0004\;=\;0,7701\).

С помощью правой колонки таблицы Брадиса со значением тангенсов можно найти котангенс. Альтернативный вариант — вычисление через тангенс угла, дополняющего искомый до 90°:

• \(ctg\;10^\circ\;=\;tg\;80^\circ\;=\;5,671\). Прибегая к помощи дополнительных колонок находим — \(сtg\;10^\circ\;12'\;=\;5,558,\;сtg\;10^\circ\;24'\;=\;5,449\) (аналогичные результаты могут быть получены, если посмотреть в значение тангенса дополняющих углов — 79° 48' и 79° 36' соответственно);
• \(ctg\;50^\circ\;=\;0,8391\). Заглянув в дополнительную колонку выясняем, что \(ctg\;50^\circ\;12'\;=\;0,8332,\;ctg\;50^\circ\;24'\;=\;0,8273\) (как вариант, можно уточнить значение тангенса дополняющих углов — 39° 48' и 39° 36').

Важно отметить, что значения тангенсов (и соответствующих им котангенсов) распределены по двум таблицам:

• тангенсы углов от 0° до 76° (и котангенсы от 90° до 24°);
• tg от 76° до 90° (и ctg от 24° до 0°).

Например, в отдельных строках таблицы, без применения поправочных величин, приводятся:

• \(tg\;80^\circ\;(и\;ctg\;10^\circ)\;=\;5,671\);
• \(tg\;80^\circ\;1'\;(и\;ctg\;10^\circ\;59')\;=\;5,681\);
• \(tg\;80^\circ\;2'\;(и\;ctg\;10^\circ\;58')\;=\;5,\;691\);
• и так далее.

Величину тангенса и котангенса можно узнать и имея в наличии только таблицу Брадиса по синусам и косинусам. Для этого надо воспользоваться формулами:

• \(tg\;\alpha\;=\;\sin\;\alpha\;/\;\cos\;\alpha\)
• \(ctg\;\alpha\;=\;\cos\;\alpha\;/\;\sin\;\alpha\).

Подставляя необходимые значения получим:

• \(tg\;10^\circ\;=\;0,1736\;/\;0,9848\;=\;0,1763\);
• \(ctg\;50^\circ\;=\;0,6428\;/\;0,7660\;=\;8391\).

Значения от 181 до 360 градусов

Таблицы Брадиса дают значения для углов от 0° до 90°. Остальные величины можно легко найти с помощью формул приведения. В этом случае угол, величину которого необходимо узнать, представляется как сумма (или разность) угла, кратного 90° и острого угла, например, для 140° это будет:

• 90° + 50°;
• 180° - 40°.

Формулы приведения, которые используются в этом случае, имеют вид:

• \(\sin\;(90^\circ\;+\;a)\;=\;\cos\;a,\;\sin\;(180^\circ\;-\;\beta)\;=\;\sin\;a\);
• \(\cos\;(90^\circ\;+\;a)\;=\;-\sin\;a,\;\cos\;(180^\circ\;-\;\beta)\;=\;-\cos\;a\);
• \(tg\;(90^\circ\;+\;a)\;=\;-ctg\;a,\;tg\;(180^\circ\;-\;\beta)\;=\;-tg\;a\);
• \(ctg\;(90^\circ\;+\;a)\;=\;-tg\;a,\;ctg\;(180^\circ\;-\;\beta)\;=\;-ctg\;a\).

Для примера можно провести расчет для ситуации, когда угол в 140° представлен как 90° + 50°:

• \(\sin\;(90^\circ\;+\;50^\circ)\;=\;\cos\;50^\circ\;=\;0,6428\);
• \(\cos\;(90^\circ\;+\;50^\circ)\;=\;-\sin\;50^\circ\;=\;-0,7660\);
• \(tg(90^\circ+50^\circ)=-ctg50^\circ=-0,8391\);
• \(ctg\;(90^\circ\;+\;50^\circ)\;=\;tg\;50^\circ\;=\;1,1918\).

Практические примеры использования таблицы

Таблицам Брадиса легко можно найти применение в современном учебном процессе, например, выполняя школьные уроки.

Задача №1

10-метровая лестница опирается на здание таким образом, что имеет угол наклона 35°. Необходимо узнать расстояние от земли до ее вершины.

Решение

Имеем треугольник, где угол BСA = 90°, BАC = 30°. По определению^

sin ВАС = ВС /АВ

где ВС — высота лестницы, которую нужно найти, а АВ — известная из условия длина.

Таким образом:

\(ВС\;=\;АВ\;х\;\sin\;ВАС\).

Узнав из таблицы Брадиса нужный синус и подставив все известные значения в формулу, можно найти ответ:

ВС (высота лестницы) = 10 м х 0,5736 =  5,736 метров.

Задача №2

Найдете длину тени от маяка высокой 30 м, если солнце находится в 60° над горизонтом.

Решение

Схематически условия задачи можно представить в виде треугольника, с прямым углом ВСА, и ВАС = 55°. По определению:

\( tg\;ВАС\;=\;АВ\;/\;СВ\)

где АВ — высота маяка, а СВ — длина тени.

Отсюда \(СВ\;=\;АВ\;/\;tg\;ВАС\).

Определив по таблице Брадиса нужную величину и подставив в формулу все известные значения, получим:

СВ (длина тени) = 30 м / 1,732 = 17,32 метра.