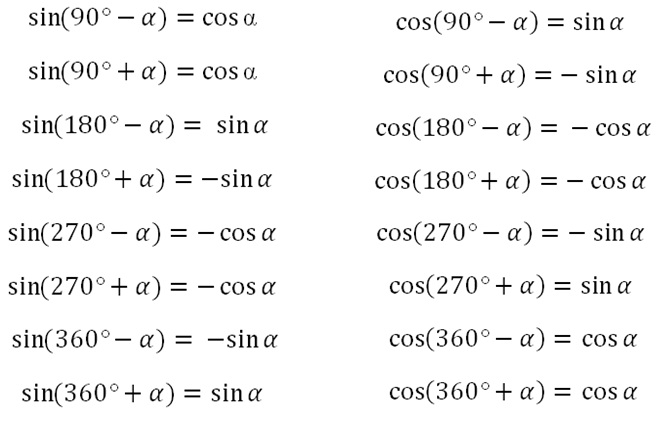Таблицы тригонометрических функций

Что такое таблицы тригонометрических функций

Для определения неизвестных элементов треугольника (сторон или углов), необходимо использовать известные элементы и правила зависимости между ними. Подобные зависимости называют также тригонометрическими функциями. Таким образом, зная значения некоторого угла или стороны, пользуясь тригонометрическими функциями можно найти неизвестные углы и стороны треугольника. Именно поэтому, без знаний тригонометрии решать геометрические задачи не представляется возможным.

Основные тригонометрические функции:

1. Синус — отношение противолежащего катета к гипотенузе.
2. Косинус — отношение прилежащего катета к гипотенузе.
3. Тангенс — отношение противолежащего катета к прилежащему. Также равен частному от деления синуса определенного угла на его косинус.
4. Котангенс — отношение прилежащего катета к противолежащему. Также равен частному от деления косинуса определенного угла на его синус.

Вычисленные тригонометрические функции (синус, косинус и тангенс) представляют в виде специальных таблиц, которые можно использовать при решении задач — это и есть таблицы тригонометрических функций. В них приведены значения тригонометрических функций углов от 0° до 360°.

Для прямоугольных треугольников в диапазоне углов от 30° до 90° тригонометрические функции равняются следующим значениям:

sin 30° = 1/2, cos 30° = √3/2, tg 30° = √3/3, ctg 30° = √3
sin 45° = √2/2, cos 45° = √2/2, tg 45°= 1, ctg 45° = 1
sin 60° = √3/2, cos 60° = 1/2, tg 60° =√3 , ctg 60° = √3/3

Как выглядит для значений, синуса, косинуса, тангенса и котангенса

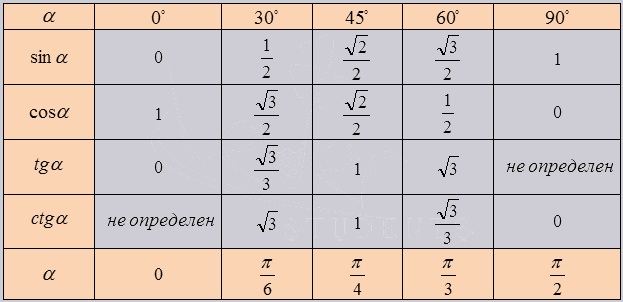
Таблица тригонометрических функций выглядит следующим образом:

Значение аргумента α задано в верхней строке задано в градусах (от 0° до 90°), во второй строке — в радианах (0, π/6, π/4, π/3, π/2 радиан). Иногда в таблице присутствуют значения только в радианах. Для перевода в градусы необходимо подставить число π = 180°, например, π/6 = 180/6 = 30°.

Обозначение «не определен» в таблице (тангенс 90° и котангенс 0°) означает, что функция является неопределенной.

Таблицы Брадиса основных тригонометрических функций

Для нахождения более точных значений тригонометрических функций острых углов (с точностью до четырех знаков после запятой) можно использовать таблицы Брадиса. За счет своей точности таблицы могут применяться как для простых задач, так и для сложных математических вычислений.

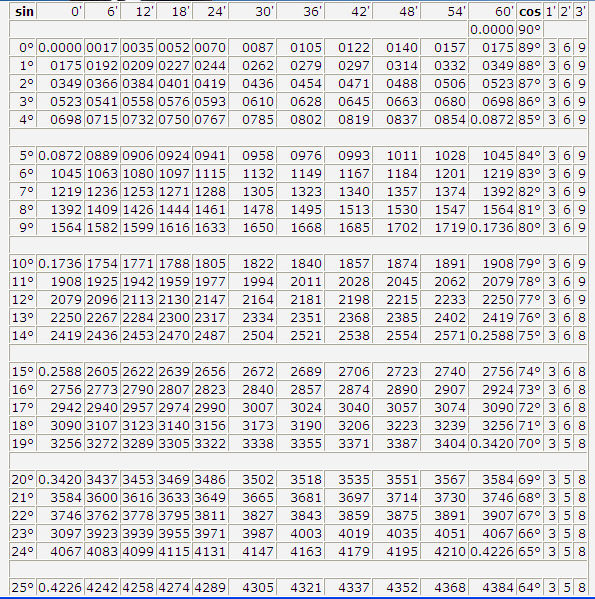
Таблица Брадиса выглядит следующим образом:

Как правильно пользоваться

Данные таблицы разделяются на несколько таблиц — отдельно для синуса, косинуса, тангенса и котангенса. С помощью, так называемых, поправок можно найти значения синусов и косинусов, не вошедшие в таблицу.

Строки таблицы показывают градусы, столбцы — доли градусов, также называемые минутами (1 градус ° равняется 60 минутам´). Таким образом, чтобы найти значение тригонометрической функции для угла X°Y´, необходимо найти пересечение строки X° и столбца Y´. В найденной ячейке будет находиться искомое значение.

В крайних правых столбцах таблицы находятся столбцы с поправками. Данные поправки используются в случае, если искомый угол отсутствует в таблице (разница — 1-3´). Чтобы найти подобный угол, необходимо найти в таблице угол, наиболее близкий к искомому, и к значению тригонометрической функции для него прибавить (для синусов) или отнять (для косинусов) значение поправки.

Так же, как и в случае с простыми таблицами тригонометрических функций, для нахождения значений функций для углов больше 90°, сначала необходимо воспользоваться формулами приведения.

Формулы приведения тригонометрических функций, таблица

Тригонометрические функции обладают свойством периодичности. Это позволяет сделать более полной таблицу со значениями от 0° до 90° с помощью формул приведения и находить значения тригонометрических функций для произвольно выбранных углов. Использование формул приведения сводится к переходу от произвольно выбранного угла к углу меньше 90°, значения которых уже можно легко найти в обычной таблице.

Формул приведения довольно много, и заучивать их, в основном, не требуют. В данных формулах аргументами тригонометрических функций обычно являются углы следующего вида:

• ±α+2π·z;
• π/2±α+2π·z;
• π±α+2π·z;
• 3π/2±α+2π·z, где z — любое натуральное число, а альфа — произвольный угол поворота.

Список формул приведения выглядит следующим образом:

В них можно использовать как градусы, так и радианы. 

Для работы с формулами приведения необходимо представить искомый угол в виде одного из перечисленных выше аргументов и подставить в формулу приведения.

Пример

Для примера возьмем угол, равный 16π/3. Его можно представить в виде π+ π/3+2 π·2, а также несколькими другими способами. Косинус данного угла в таком случае будет равен:

cos(16π/3) = cos(π+ π/3+2 π·2) = cos(π/3)

Данное значение мы уже можем найти в обычной таблице тригонометрических функций, значение cos(π/3) = 1/2.

На основе формул приведения можно составить расширенную таблицу тригонометрических функций. В расширенную таблицу входят значения тригонометрических функций для углов 0°, 30°, 60°, ...,120°, 135°, 150°, 180°, ..., 360° (им соответствуют значения 0, π/6, π/3, π/2, …, 2π радиан).