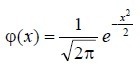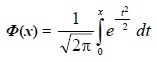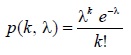Применение локальной и интегральной теоремы Муавра-Лапласа

Локальная и интегральная теоремы Муавра-Лапласа

В том случае, когда количество манипуляций достаточно большое, применять формулу Бернулли становится нецелесообразно. Упростить решение задачи или доказательство выражения можно с помощью локальной и интегральной теорем Лапласа. Данные закономерности позволяют получить результат испытаний, приближенный к итогам вычислений по формуле Бернулли, и характеризуются меньшими расчетами.

Рассматриваемые теоремы активно применяют в решении задач по данным большого количества экспериментов для нахождения приближенного значения вероятности. С помощью локальной теоремы можно вычислить определенное число явлений. Благодаря интегральной теореме Муавра-Лапласа, достаточно просто найти ответ при заданном диапазоне вероятного количества возникновения событий.

Локальная теорема Лапласа

В данном случае\( x=\frac { k-n\cdot p } { \sqrt { n\cdot p\cdot q } }\)

Из выражения можно сделать вывод:

\(label { eq2 } P_n ( k )\approx \frac { 1 } { \sqrt { n\cdot p\cdot q } } \cdot \varphi ( x )\)

где \(x=\frac { k-n\cdot p } { \sqrt { n\cdot p\cdot q } }\)

Следует отметить, что функция \(\varphi ( x )=\varphi ( { -x } )\) является четной.

Свойства представленной функции:

• функция является четной;
• если аргумент обладает значением больше, чем 4, то функция будет сколь угодно мала.

Интегральная предельная теорема Муавра-Лапласа

В смысле данной формулировки,\( x_1 =\frac { k_1 -n\cdot p } { \sqrt { n\cdot p\cdot q } }\) , \(x_2 =\frac { k_2 -n\cdot p } { \sqrt { n\cdot p\cdot q } }\)

Следует отметить, что \(\Phi ( x )=\frac { 1 } { \sqrt { 2\cdot \pi } } \int { e^ { - { z^2 } / 2 } dz }\) можно определить с помощью специальных табличных схем.

\(\Phi ( { -x } )=-\Phi ( x )\) является нечетной функцией.

Рассматриваемая функция обладает следующими основными свойствами:

• функция является нечетной;
• если аргумент больше, чем 5, то значение функции составляет 0,5.

Таблица значений для вычисления определителей

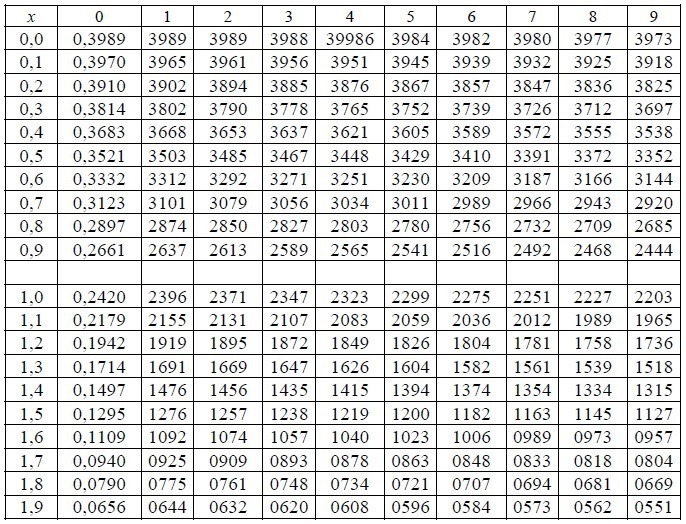
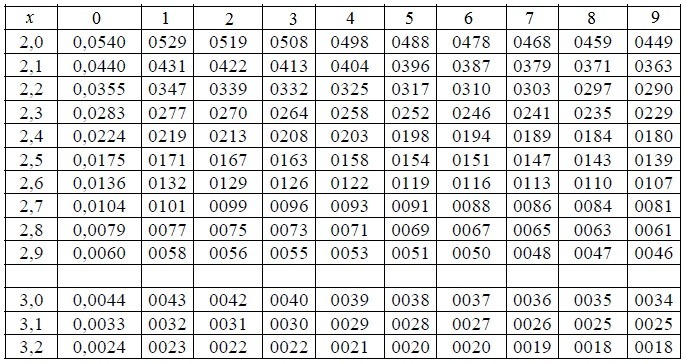
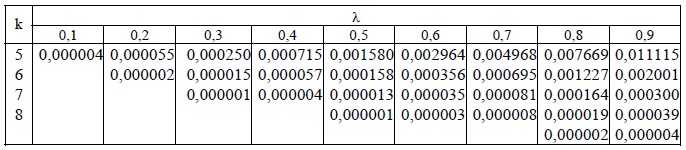
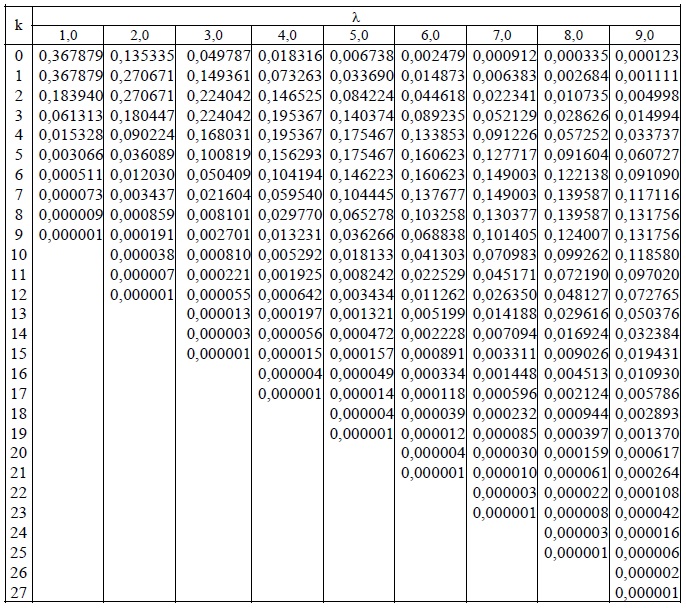
В случае применения локальной теории Лапласа целесообразно использовать специальные таблицы:

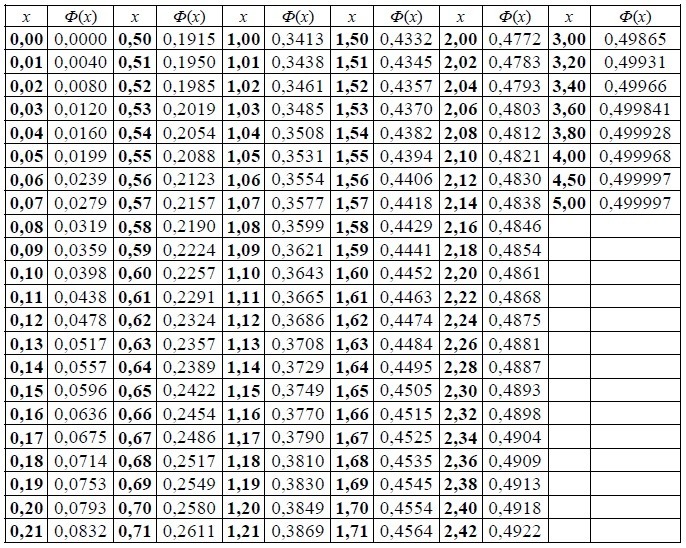
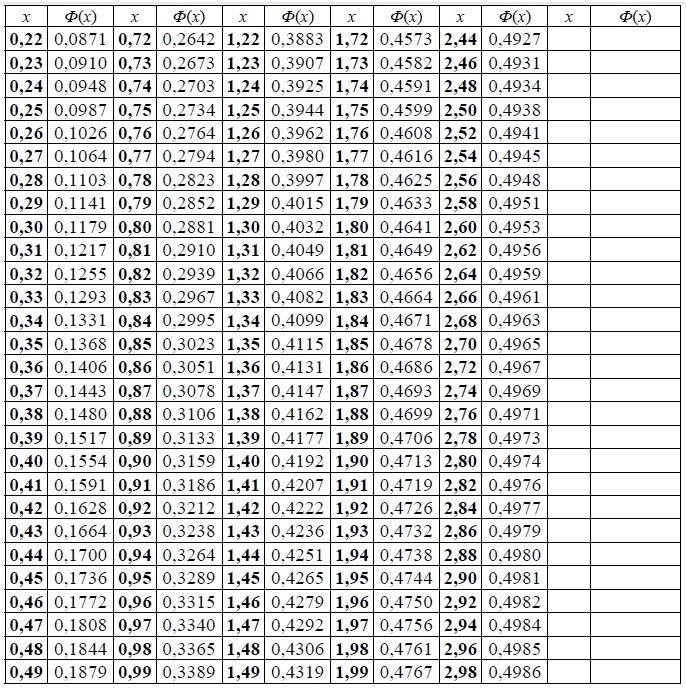
Таблица значений интегральной функции Лапласа имеет следующий вид:

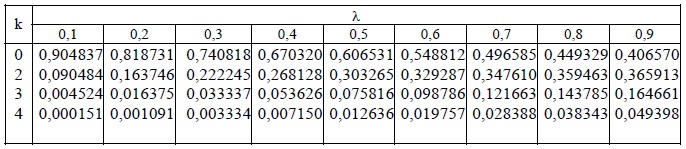
Применительно к вероятностям распределения Пуассона сформирована таблица:

Источник: ekonomika-st.ru

Источник: ekonomika-st.ru

Источник: ekonomika-st.ru

Источник: ekonomika-st.ru

Пример решения задачи

Решение:

В том случае, когда р = 0,2: q = 1 – p = 1 – 0,2 = 0,8

Таким образом:

\(P_ { 400 } ( { 80 } )\approx \frac { 1 } { \sqrt { n\cdot p\cdot q } } \varphi ( x )\,,\,\)

где \(x=\frac { k-n\cdot p } { \sqrt { n\cdot p\cdot q } }\)

В таком случае:

\(\begin{array} { l } x=\frac { k-n\cdot p } { \sqrt { n\cdot p\cdot q } } =\frac { 80-400\cdot 0,2 } { \sqrt { 400\cdot 0,2\cdot 0,8 } } =\frac { 80-80 } { \sqrt { 400\cdot 0,16 } } =0 \\ \varphi ( 0 )=0,3989\,,\,P_ { 400 } ( { 80 } )\approx \frac { 0,3989 } { 20\cdot 0,4 } =\frac { 0,3989 } { 8 } =0,0498 \\ \end{array}\)

Ответ: вероятность равна 0,0498

Решение:

В том случае, когда брак составляет 10% от изделий, то качественные экземпляры должны определяться, как 90%. При таком условии:

\(n=625, \ p=0,9, \ q=0,1, \ k_1 =550,\ k_2 =575\)

Тогда:

\(n\cdot p=625\cdot 0,9=562,5\)

Исходя из полученного выражения, определим:

\(\begin{array} { l } P_ { 625 } (550,575)\approx \Phi ( { \frac { 575-562,5 } { \sqrt { 625\cdot 0,9\cdot 0,1 } } } )- \Phi ( { \frac { 550-562,5 } { \sqrt { 626\cdot 0,9\cdot 0,1 } } } )\approx \Phi (1,67)- \Phi (-1,67)=2 \Phi (1,67)=0,9052 \\ \end{array}\)

Ответ: вероятность составит 0,9052