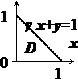Вычисление тройного интеграла
Что такое тройной интеграл
В процессе решения задач по алгебре, геометрии, физике и другим дисциплинам часто встречается такое понятие как интеграл. С помощью интегрирования можно упростить достаточно громоздкие и сложные расчеты. Отдельно стоит рассмотреть тройной интеграл. При формулировке термина и расшифровке его смысла целесообразно воспользоваться алгоритмом действий, аналогичным введению понятия двойного интеграла.
Предположим, что имеется некоторая функция. Обозначим ее как \(u=f\left( x;\ y;\ z \right)\). Введем условие, по которому область определения рассматриваемой функции соответствует ограниченной области \(\Omega\) в трехмерном измерении и декартовой системой с координатами по осям \(Oxyz\). В замкнутом пространстве можно выделить некоторое количество фрагментов, равное n частям \({{\Omega }_{i}}\). Эти сегменты не обладают едиными точками внутри области, а для вычисления их объемов стоит воспользоваться соотношением:
\(\Delta {{V}_{i}},\ i=\overline{1;\ n}\).
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
На следующем шаге необходимо отметить в каждой из выделенных ранее частей какую-либо точку \({{P}_{i}}\left( {{x}_{i}};\ {{y}_{i}};\ {{z}_{i}} \right)\). Используя записанное выражение, несложно сформулировать соотношение для интегральной суммы в случае конкретной функции \(u=f\left( x;\ y;\ z \right)\) по области \(\Omega\). Выражение примет следующий вид:
\(\sum\limits_{i=1}^{n}{f\left( {{x}_{i}};\ {{y}_{i}};\ {{z}_{i}} \right)\Delta {{V}_{i}}}\)
Рассмотрим детально фрагменты ограниченного пространства, которые записаны как \({{\Omega }_{i}}\). Эти простейшие части имеют точки, которые ранее были обозначены, удаленные друг от друга на расстояние, вычисляемое по формуле:
\(\lambda =\underset{1\le i\le n}{\mathop{\max }}\,d\left( {{\Omega }_{i}} \right)\)
Допустим, что имеется некий предел: \(\underset{\lambda \to 0}{\mathop{\lim }}\,\sum\limits_{i=1}^{n}{f\left( {{x}_{i}};\ {{y}_{i}};\ {{z}_{i}} \right)\Delta {{V}_{i}}}.\)
Этот предел определен вне зависимости от метода деления области пространства \(\Omega\) на простейшие части \({{\Omega }_{i}}\). Значение также не имеет обозначение в рассматриваемых фрагментах точек \({{P}_{i}}\). Если перечисленные условия выполнимы, то записанный предел является тройным интегралом по области \(\Omega\). При обозначении данного понятия целесообразно обратиться к такому соотношению:
\(\iiint\limits_{\Omega }{f(x;y;z)dV} \text{ }\text{ } , \text{ }\text{ } \iiint\limits_{\Omega }{f(x;y;z)dxdydz}\)
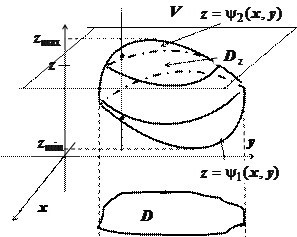
Из уже рассмотренного примера можно заключить, что область \Omega ограничена в пространстве. Представим, что на нижней и верхней границе расположены следующие поверхности:
- \(z={{\phi }_{1}}\left( x;\ y \right)\);
- \(z={{\phi }_{2}}\left( x;\ y \right)\).
В соответствии с этой информацией \(({{\phi }_{2}}\left( x;\ y \right)\ge {{\phi }_{1}}\left( x;\ y \right))\). С боковых сторон относительно исследуемой области находится поверхность в форме цилиндра, образующие которой расположены параллельно по отношению к оси Oz. В плоскости D можно наблюдать изменения переменных х и у. Данную плоскую область допустимо считать проекцией \(\Omega\) на плоскость с координатами Оху.
С целью определения элемента объема dv в условиях декартовой координатной системы стоит воспользоваться следующим соотношением: \(dv=dxdydz\). Таким образом, в случае рассматриваемого ограниченного пространства \(\Omega\) тройной интеграл соответствует справедливому равенству:
\(\iiint\limits_{\Omega}{f(x; y; z)dxdydz}=\iint\limits_{D}{dxdy}\int\limits_{{{\phi }_{1}}\left( x \right)}^{{{\phi }_{2}}\left( x \right)}{f\left( x;\ y;\ z \right)dz}\)
Заметим, что интеграл внутри выражения \(\int\limits_{{{\phi }_{1}}\left( x \right)}^{{{\phi }_{2}}\left( x \right)}{f\left( x;\ y;\ z \right)dz}\) зависит и рассчитывается с учетом значения, которое принимает z. При этом х и у не меняют свои значения. В итоге операции интегрирования получают функцию переменных х и у, которую можно обозначить за \(F\left( x;y \right)\) . Таким образом, алгоритм определения тройного интеграла представляет собой процесс расчета двойного интеграла \(\iint\limits_{D}{F\left( x;\ y \right)dxdy}\). Стоит отметить, что допустимо нахождение внутреннего интеграла по х или по у, что формирует определенный порядок действий при интегрировании.
Свойства тройного интеграла
Тройной интеграл обладает рядом характерных свойств. Такие закономерности позволяют существенно упростить и сократить объем расчетов в процессе интегрирования. Каждая из характеристик сопровождается формулой или соотношением. Сформулированные математические записи применимы к условиям какой-либо задачи. При поиске ответа нужно лишь привести расчеты под установленный формат записи или подставить в готовую формулу известные значения для вычисления искомых величин.
Тройной интеграл имеет следующие свойства:
- Линейность. Когда некоторая функции \(\mathbf { \textit { f } } (\mathbf { \textit { x } }, \mathbf { \textit { y } }, \mathbf { \textit { z } } ), \mathbf { \textit { g } } (\mathbf { \textit { x } }, \mathbf { \textit { y } }, \mathbf { \textit { z } } )\) можно найти через интегралы по ограниченному пространству \(\mathbf { \textit { V } }\), линейная комбинация рассматриваемых функций \(\alpha f(x,y,z)+\beta g(x,y,z)\) аналогично поддается интегрированию по \(\mathbf { \textit { V } }, а также \iiint\limits_V { \,\left[ { \alpha f(P)+\beta g(P) }\right]dv } = \alpha \iiint\limits_V { f(P)dv } +\beta \iiint\limits_V { g(P)dv }.\)
- Аддитивность. При условии, что некоторое ограниченное пространство \(\mathbf { \textit { V } }\) представляет собой совмещение пары областей \(\mathbf { \textit { V } } _ { 1 } и \mathbf { \textit { V } } _ { 2 }\) , которые не обладают едиными точками, выполняется следующее равенство: \(\iiint\limits_V { f(P)dv } =\iiint\limits_ { V_1 } { f(P)dv } +\iiint\limits_ { V_2 } { f(P)dv }\).
- Интеграл от единичной функции по области можно рассчитать, используя такое соотношени \(\mathbf { \textit { V } } \quad \textbf { равен объёму этой области: } \iiint\limits_V { dv } =v(V)\textbf { . }\)
- Интегрирование неравенств. Представим, что для каких-либо точек \(P\in V\) справедливо выражение со знаком неравенства \(f(P)\leqslant g(P)\), а также функции \(\mathbf { \textit { f } } (\mathbf { \textit { P } } ), \mathbf { \textit { g } } (\mathbf { \textit { P } } ) \) можно интегрировать относительно ограниченного пространства \(\mathbf { \textit { V } }\). В таком случае \(\iiint\limits_V { f(P)dv } \leqslant \iiint\limits_V { g(P)dv }\).
- Теоремы об оценке интеграла. В той ситуации, когда функция \(\mathbf { \textit { f } } (\mathbf { \textit { P } } )\)имеет интеграл по некоторому ограниченному пространству \(\mathbf { \textit { V } }\), а также при условии \(\forall P\in V \) справедливо, что \(m\leqslant f(P)\leqslant M\), работает следующее соотношение \(m\cdot v(V)\leqslant \iiint\limits_V { f(P)dv } \leqslant M\cdot v(V)\). При условии, что функцию \(\mathbf { \textit { f } } (\mathbf { \textit { P } } )\) допустимо интегрировать по области \(\mathbf { \textit { V } }\) , можно записать такое выполняемое выражение \(\left| { \iiint\limits_V { f(P)dv } }\right|\leqslant \iiint\limits_V { \,\vert f(P)\vert dv }\).
- Теорема о среднем. Когда исследуемая функция \(\mathbf { \textit { f } } (\mathbf { \textit { P } } )\) не прерывается на области \(\mathbf { \textit { V } }\), можно говорить о существовании некоторой точки \(P_0 \in V\), при наличии которой выполняется следующее равенство \(\iiint\limits_V { f(P)dv } =f(P_0 )\cdot v(V)\).
Геометрический смысл тройного интеграла, как вычислить
Заметим, что в процессе определения тройного интеграла речь идет о поиске числа, выражающего объем некоторой фигуры V, то есть фактически ограниченного пространства V. В этом заключается геометрический смысл тройного интеграла. С помощью рассмотренного ранее понятия достаточно просто вычислить объем какого-то тела, относительно которого рассчитывается этот интеграл.
Процесс интегрирования очень интересен с прикладной точки зрения. Например, рассмотреть понятие можно с помощью изучения работы органов дыхания человека, а именно, легких. Известно, что эти функциональные и жизненноважные структуры включают в себя более семи сотен миллионов альвеол, которые представляют собой пузырьки, защищенные капиллярными сетками. Данные образования обеспечивают необходимый газовый обменный процесс.
Представим, что объем газообразного вещества во внутреннем пространстве легких является какой-то ограниченной областью с компактными размерами. В этот объем включено некоторое количество объемов габаритами поменьше, то есть альвеол. Смысл этого сравнения заключается во множестве пузырьковых образований, составляющих объем дыхательных органов. Таким образом, большое число малостей с точки зрения математики определяет значение термина тройного интеграла.
Предположим, что имеется некоторое замкнутое пространство с границами. Обозначим его как V. Такая область считается простейшей правильной при выполнении пары условий:
- проекция \(\mathbf { \textit { V } }\) на некоторую плоскость с координатами, в том числе, \(\mathbf { \textit { Оху } }\), представляет собой простую область \(\mathbf { \textit { D } }\);
- произвольная прямая линия, расположенная перпендикулярно относительно рассматриваемой плоскости, пересекает точку \(\mathbf { \textit { V } }\)внутри области и границу \(\mathbf { \textit { V } }\) в паре точек.
Тогда справедливым является следующее выражение:
\(V=\left( { (x,y,z)\vert (x,y)\in D,\;\psi _1 (x,y)\leqslant z\leqslant \psi _2 (x,y) }\right)\)
При этом целесообразно выделить пару граничных поверхностей:
- \(z=\psi _1 (x,y)\);
- \(z=\psi _2 (x,y)\).
Источник: 3dstroyproekt.ru
При условии наличия некоторой примитивной области \(\mathbf { \textit { V } }\), граница которой является кусочно-гладкой, а функция \(\mathbf { \textit { f } } (\mathbf { \textit { P } } )\) не прерывается, можно заключить, что: \(\iiint\limits_V { f(P)dv } =\iint\limits_D { dxdy\int\limits_ { \psi _1 (x,y) } ^ { \psi _2 (x,y) } { f(x,y,z)dz } }\) .
Исходя из записанной теоремы и полезных свойств, перечисленных ранее, допустимо представить следующую формулу для расчета тройного интеграла:
\(\iiint\limits_V { f(P)dv } =\iint\limits_D { dxdy\int\limits_ { \psi _1 (x,y) } ^ { \psi _2 (x,y) } { f(x,y,z)dz } } =\int\limits_a^b { dx\int\limits_ { \varphi _1 (x) } ^ { \varphi _2 (x) } { dy\int\limits_ { \psi _1 (x,y) } ^ { \psi _2 (x,y) } { f(x,y,z)dz } } }.\)
Если при решении задачи требуется сформулировать тройной интеграл через двойной, но при измененном порядке интегрирования, то целесообразно обратиться к такому соотношению:
\(\iiint\limits_V { f(P)dv } =\int\limits_ { z_ { \min } } ^ { z_ { \max } } { dz\iint\limits_ { D_z } { f(x,y,z) } } dxdy.\)
В теоретическом материале достаточно емко изложен смысл тройного интеграла. Однако при решении практических заданий порой сложно сразу сориентироваться в применении той или иной формулы интегрирования. Важно владеть основными приемами вычисления тройного интеграла и помнить о характерных для этого понятия свойствах, которые помогают справиться с самыми сложными примерами.
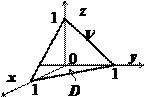
С применением понятия и свойств интегрирования необходимо вычислить следующий пример: \(I=\iiint\limits_V { \frac { dxdydz } { \left( { 1+x+y+z }\right)^3 } } ,\;V:\left[{ \begin{array} { l } x=0,\;y=0,\;z=0, \\ x+y+z=1. \\ \end{array} }\right.\)
К заданию прилагается рисунок для наглядной демонстрации описанных в задаче величин:
Источник: 3dstroyproekt.ru
Решение
Заметим, что при проектировании фрагмента ограниченного пространства \(\mathbf { \textit { V } }\) на плоскость \(\mathbf { \textit { Оху } }\) получается геометрическая фигура в виде треугольника \(D:\left[{ x=0,\;y=0,\;x+y=1 }\right]\). Исходя из этого, запишем следующее справедливое соотношение:
\(I=\iiint\limits_V { \frac { dxdydz } { \left( { 1+x+y+z }\right)^3 } } =\iint\limits_D { dxdy\int\limits_0^ { 1-x-y } { \frac { dz } { (1+x+y+z)^3 } } } =\iint\limits_D { \left. { \left[ { -\frac { 1 } { 2 } \cdot \frac { 1 } { (1+x+y+z)^2 } }\right] }\right|_0^ { 1-x-y } dxdy }\)
Для наглядности представим такое изображение:
Источник: 3dstroyproekt.ru
Продолжим вычисления:
\(I=-\frac { 1 } { 2 } \int\limits_0^1 { dx } \int\limits_0^ { 1-x } { \left[ { \frac { 1 } { 4 } -\frac { 1 } { (1+x+y)^2 } }\right]dy } =-\frac { 1 } { 2 } \int\limits_0^1 { \left. { \left[ { \frac { y } { 4 } +\frac { 1 } { 1+x+y } }\right] }\right|_0^ { 1-x } dx } =-\frac { 1 } { 2 } \int\limits_0^1 { \left[ { \frac { 1-x } { 4 } +\frac { 1 } { 2 } -\frac { 1 } { 1+x } }\right]dx } = \\ =-\frac { 1 } { 2 } \int\limits_0^1 { \left[ { \frac { 1-x } { 4 } +\frac { 1 } { 2 } -\frac { 1 } { 1+x } }\right]dx } =-\frac { 1 } { 2 } \left( { \frac { 3x } { 4 } -\frac { x^2 } { 8 } -\ln (1+x) }\right)_0^1 =-\frac { 1 } { 2 } \left( { \frac { 3 } { 4 } -\frac { 1 } { 8 } -\ln 2 }\right)=\frac { 1 } { 2 } \left( { \ln 2-\frac { 5 } { 8 } }\right)\)
Ответ: \(\frac { 1 } { 2 } \left( { \ln 2-\frac { 5 } { 8 } }\right)\).
Известно, что ограниченный фрагмент пространства обозначен за \(\Omega\). Эта область имеет форму геометрической фигуры тетраэдра, граница которого представляет собой плоскость \(2x+2y+z-6=0\). Остальные границы являются плоскостями с координатами. Требуется определить значение тройного интеграла: \(I=\iiint\limits_{\Omega }{xdxdydz}\) I
Решение
\(I=\int\limits_{0}^{3}{dx}\int\limits_{0}^{3-x}{dy}\int\limits_{0}^{6-2x-2y}{xdz}=\int\limits_{0}^{3}{xdx}\int\limits_{0}^{3-x}{\left. z_{{}}^{{}} \right|_{0}^{6-2x-2y}dy}=\int\limits_{0}^{3}{xdx}\int\limits_{0}^{3-x}{\left( 6-2x-2y \right)dy}= \int\limits_{0}^{3}{x\left. \cdot \left( 6y-2xy-{{y}^{2}} \right) \right|_{0}^{3-x}dx}=\int\limits_{0}^{3}{x\left( 6\left( 3-x \right)-2x\left( 3-x \right)-{{\left( 3-x \right)}^{2}} \right)dx=} \int\limits_{0}^{3}{\left( {{x}^{3}}-6{{x}^{2}}+9x \right)dx=}\left. \left( \frac{{{x}^{4}}}{4}-\frac{6{{x}^{3}}}{3}+\frac{9{{x}^{2}}}{2} \right) \right|_{0}^{3}=\frac{81}{4}-54+\frac{81}{2}=\frac{27}{4}.\)
Ответ: \(\frac{27}{4}\).
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так