Возрастание и убывание функции
Что такое возрастающие и убывающие функции
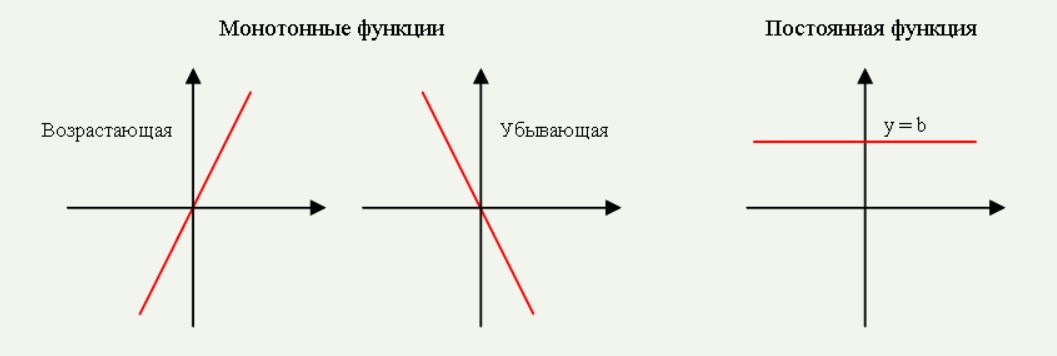
Монотонная функция — функция, изменяющаяся исключительно в одном и том же направлении.
И убывающая, и возрастающая функции относятся именно к понятию монотонной.
Возрастающая функция — линейная функция, возрастающая при увеличении значения аргумента.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Убывающая функция — линейная функция, убывающая при увеличении значения аргумента.
Также важно знать, что существует постоянная функция, значение которой не меняется на всем промежутке графика.
Свойства и признаки, пример
Достаточными условиями для возрастания или убывания функций являются следующие признаки:
- Если производная y=f(x)>0 для любого x из интервала X, то f возрастает на X.
- Если производная y=f(x)<0 для любого x из интервала X, то f убывает на X.
Кроме этого, у монотонных функций есть характерные особенности, называемые свойствами. Они помогают в решении задач различной сложности: начиная от функций с логарифмами и заканчивая неравенствами с функциями. Свойства:
- Если функции f и g возрастают/убывают на интервале (a,b), то их сумма также возрастает/убывает на этом интервале.
- Если функция f возрастает/убывает на интервале (a,b), то функция -f убывает/возрастает на этом интервале.
- Если функция f возрастает/убывает на интервале (a,b), то функция \frac1f убывает/возрастает на этом интервале.
- Если функции f и g возрастают/убывают на интервале (a,b), а f≥0, g≥0, то f\times g также возрастает/убывает на этом интервале.
- Если функция g возрастает/убывает на интервале (a,b), а функция f возрастает/убывает на интервале (c,d), где g:(a,b)\(\rightarrow\)(c,d), то сложная функция y=f(g(x)) также возрастает/убывает на интервале (a,b).
Пример:
Рассмотрим пример-доказательство для убывающей функции:
Доказать, что f(x)=x2+1 возрастает при \(x\geq0\).
Возьмем точки x1 и x2, чтобы \(0\leq x_1\leq x_2.\) Посмотрим на разность значений функции в данных точках.
\(f(x_2)-f(x_1)=({x^2}_2+1)-({x^2}_1+1)={x^2}_2-x_1^2=(x_2-x_1)\times(x_2+x_1).\)
Видим, что \(x_2-x_1>0 \) и \( x_2+x_1>0\). Следовательно, \(f(x)=x^2+1\) — возрастающая.
ЧТД.
Возрастающими являются также следующие функции:
- \(y=a(x), (a>0);\)
- \(y=a^x, (a>1);\)
- \(y=\log_a\left(x\right), (a>1).\)
Убывающими же являются функции:
- \(y=a(x), (a<0);\)
- \(y=a^x, (0<a<1);\)
- \(y=\log_a\left(x\right), (0<a<1).\)
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так