Как найти угол между векторами
Угол между векторами
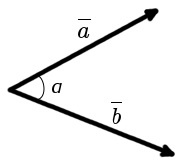
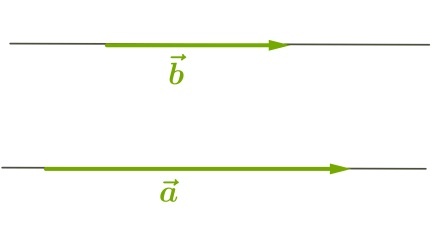
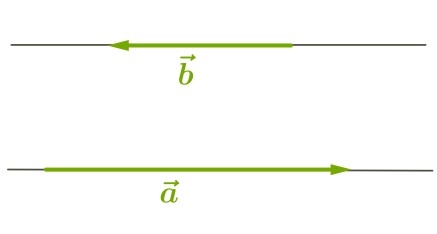
Угол между векторами — это угол между отрезками, которые изображают эти две направляющие и которые отложены от одной точки пространства. Другими словами — это кратчайший путь, на который можно повернуть один из векторов вокруг его начала до положения общей направленности со вторым.
На изображении это α, который также можно обозначить следующим образом:
\(\left(\widehat{\overrightarrow a;\overrightarrow b}\right)\)
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Как и любой другой угол, векторный может быть представлен в нескольких вариациях.
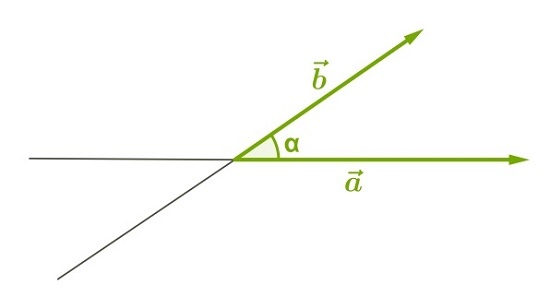
Острый:
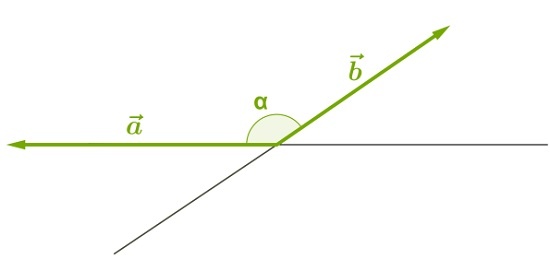
Тупой:
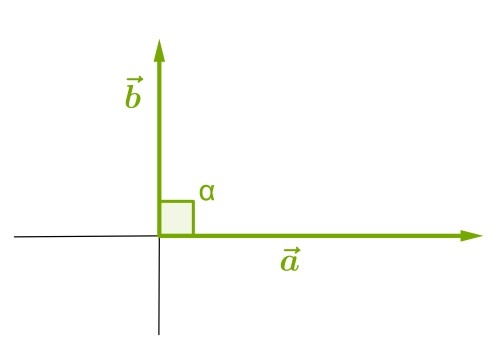
Прямой:
С величиной \(0^\circ\) (то есть, векторы сонаправлены):
С величиной \(180^\circ\) (векторы направлены в противоположные стороны):
Нахождение угла между векторами
Как правило, угол между \( \overrightarrow a\) и \(\overrightarrow b\) можно найти с помощью скалярного произведения или теоремы косинусов для треугольника, который был построен на основе двух этих направляющих.
Скалярное произведение — это число, которое равно произведению двух направляющих на косинус угла между ними.
Формула скалярного произведения:
\(\left(\overrightarrow a;\overrightarrow b\right)=\left|\overrightarrow a\right|\times\left|\overrightarrow b\right|\times\cos\left(\widehat{\overrightarrow a;\overrightarrow b}\right)\)
- Если α — острый, то СП (скалярное произведение) будет положительным числом (cos острого угла — положительное число).
- Если векторы имеют общую направленность, то есть угол между ними равен \(0^\circ\), а косинус — 1, то СП будет тоже положительным.
- Если α — тупой, то скалярное произведение будет отрицательным (cos тупого угла — отрицательное число).
- Если α равен \(180^\circ\), то есть векторы противоположно направлены, то СП тоже отрицательно, потому что cos данного угла равен 1.
- Если α — прямой, то СП равно 0, так как косинус \(90^\circ\) равен 0.
В случае, если \overrightarrow a и \overrightarrow b не нулевые, можно найти косинус α между ними, опираясь на формулу:
\(\cos\left(\widehat{\overrightarrow a;\overrightarrow b}\right)=\frac{\left(\overrightarrow a;\overrightarrow b\right)}{\left|\overrightarrow a\right|\times\left|\overrightarrow b\right|}\)
Расчет угла, если вектор задан координатами
В случае, когда направляющие расположены на двухмерной плоскости с заданными координатами в виде \(\overrightarrow a=\left(a_x;a_y\right)\) и \(\overrightarrow b=\left(b_x;b_y\right)\), то угол между ними можно найти следующим образом:
\(\cos\left(\widehat{\overrightarrow a;\overrightarrow b}\right)=\frac{\left(\overrightarrow a;\overrightarrow b\right)}{\left|\overrightarrow a\right|\times\left|\overrightarrow b\right|}=\frac{a_x\cdot b_x+a_y\cdot b_y}{\sqrt{a_x^2+a_y^2}\cdot\sqrt{b_x^2+b_y^2}}\)
Если же координаты находятся в трехмерном пространстве и заданы в виде:
\(\overrightarrow a=\left(a_x;a_y;a_z\right)\)
\( \overrightarrow b=\left(b_x;b_y;b_z\right)\)
то формула принимает такой вид:
\(\cos\left(\widehat{\overrightarrow a;\overrightarrow b}\right)=\frac{\left(\overrightarrow a;\overrightarrow b\right)}{\left|\overrightarrow a\right|\times\left|\overrightarrow b\right|}=\frac{a_x\cdot b_x+a_y\cdot b_y+a_z\cdot b_z}{\sqrt{a_x^2+a_y^2+a_z^2}\cdot\sqrt{b_x^2+b_y^2+b_z^2}}\)
Расчет угла, если заданы три точки в прямоугольной системе координат
В этом случае проще будет разобраться с объяснениями сразу на примере.
Допустим, нам известны три точки и их координаты: A(3,-2), B(2,1), C (6,-1). Нужно найти косинус угла между \(\overrightarrow{AC}\) и \(\overrightarrow{BC}\).
Решение
Для начала найдем их координаты по известным координатам заданных точек:
\(\overrightarrow{AC}=(6-3, -1-(-2))=(3,1)\)
\(\overrightarrow{BC}=(6-2, -1-1)=(4,-2)\)
После этого уже можем применить формулу для определения косинуса угла на плоскости и подставить известные значения:
\(\cos\left(\widehat{\overrightarrow{AC};\overrightarrow{BC}}\right)=\frac{(\overrightarrow{AC};\;\overrightarrow{BC})}{\left|\overrightarrow{AC}\right|\cdot\left|\overrightarrow{BC}\right|}=\frac{3\cdot4+1\cdot(-2)}{\sqrt{3^2+1^2}\cdot\sqrt{4^2+{(-2)}^2}}=\frac{10}{\sqrt{10}\cdot2\sqrt5}=\frac{10}{10\sqrt2}=\frac1{\sqrt2}\)
Ответ: \(\cos\left(\widehat{\overrightarrow{AC};\overrightarrow{BC}}\right)=\frac1{\sqrt2}.\)
Примеры решения задач
Для наглядности, взглянем на примеры решения задач по данной теме.
Задача 1
Известно, что \(\overrightarrow a\) и \(\overrightarrow b\). Их длины равны 3 и 6 соответственно, а скалярное произведение равно -9. Нужно найти cos угла между векторами и его величину.
Решение
Применим формулу:
\( \cos\left(\widehat{\overrightarrow a;\overrightarrow b}\right)=\frac{\left(\overrightarrow a;\overrightarrow b\right)}{\left|\overrightarrow a\right|\times\left|\overrightarrow b\right|}\)
Подставим известные значения:
\(\cos\left(\widehat{\overrightarrow a;\overrightarrow b}\right)=\frac{-9}{3\cdot6}=-\frac12\)
Далее найдем угол между данными векторами:
\(arc\cos\left(-\frac12\right)=\frac{3\pi}4\)
Ответ: \(\left(\widehat{\overrightarrow a;\overrightarrow b}\right)=-\frac12,\;\left(\widehat{\overrightarrow a;\overrightarrow b}\right)=\frac{3\pi}4.\)
Задача 2
В пространстве даны координаты \(\overrightarrow a=(8; -11; 7)\) и \(\overrightarrow b=(-2; -7; 8)\). Вычислить угол α между ними.
Решение
Используем формулу для нахождения косинуса угла между направляющими в трехмерной системе координат:
\(\cos\left(\widehat{\overrightarrow a;\overrightarrow b}\right)=\frac{\left(\overrightarrow a;\overrightarrow b\right)}{\left|\overrightarrow a\right|\times\left|\overrightarrow b\right|}=\frac{a_x\cdot b_x+a_y\cdot b_y+a_z\cdot b_z}{\sqrt{a_x^2+a_y^2+a_z^2}\cdot\sqrt{b_x^2+b_y^2+b_z^2}}\)
Подставляем значения и получаем:
\(\cos\left(\alpha\right)=\frac{8\cdot(-2)+(-11)\cdot(-7)+7\cdot8}{\sqrt{8^2+{(-11)}^2+7^2}\cdot\sqrt{{(-2)}^2+{(-7)}^2+8^2}}=\frac{117}{\sqrt{234}\cdot\sqrt{117}}=\frac{\sqrt{117}}{\sqrt{234}}=\frac1{\sqrt2}=\frac2{\sqrt2}\)
Теперь находим угол α:
\(\alpha=arc\cos\left(\frac2{\sqrt2}\right)=45^\circ\)
Ответ: \(45^\circ\).
Задача 3
Известны \(\overrightarrow a=(3; 4)\) и \(\overrightarrow b=(2; 5)\). Найти угол между ними.
Решение
Для расчета используем формулу:
\(\cos\left(\widehat{\overrightarrow a;\overrightarrow b}\right)=\frac{\left(\overrightarrow a;\overrightarrow b\right)}{\left|\overrightarrow a\right|\times\left|\overrightarrow b\right|}=\frac{a_x\cdot b_x+a_y\cdot b_y}{\sqrt{a_x^2+a_y^2}\cdot\sqrt{b_x^2+b_y^2}}\)
Подставим известные значения и получим:
\(\cos\left(\widehat{\overrightarrow a;\overrightarrow b}\right)=\frac{\left(\overrightarrow a;\overrightarrow b\right)}{\left|\overrightarrow a\right|\times\left|\overrightarrow b\right|}=\frac{a_x\cdot b_x+a_y\cdot b_y}{\sqrt{a_x^2+a_y^2}\cdot\sqrt{b_x^2+b_y^2}}=\frac{3\cdot2+4\cdot5}{\sqrt{3^2+4^2}\cdot\sqrt{2^2+5^2}}=\frac{26}{\sqrt{25}\cdot\sqrt{29}}=\frac{26}{5\sqrt{29}}\)
Ответ: \(\cos\left(\widehat{\overrightarrow a;\overrightarrow b}\right)=\frac{26}{5\sqrt{29}}\)
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так