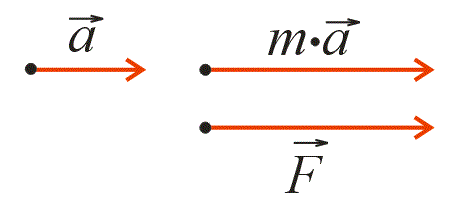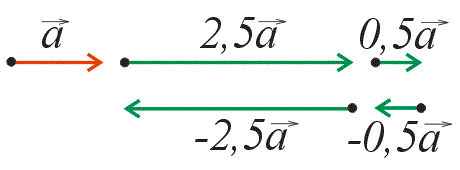Умножение вектора на число

Возможно ли умножение вектора на число

Произведением вектора \(\bar{a}\), не равного нулю, на число \(\lambda \ne 0\) является вектор \(\lambda \bar{a},\) коллинеарный заданному, то есть он будет сонаправлен данному вектору \(\bar{a}\), если \(\lambda>0\), и противоположно направленным — если \(\lambda<0\), а его модуль равен модулю данного вектора, умноженному на модуль числа:

\(\lambda >0:\lambda \bar{a}\uparrow \uparrow \bar{a}\)

\(\lambda <0:\lambda \bar{a}\uparrow \downarrow \bar{a}\)

\(\left|\lambda \bar{a}\right|=\left|\lambda \right|\cdot \left|\bar{a}\right|\)

В том случае, когда вектор \(\bar{a}\ne \bar{0}\) задают с помощью координат, то произведение этого вектора на число \(\lambda \ne 0\) является вектором \(\lambda \bar{a}\) с координатами, равными соответствующим координатам заданного вектора \(\bar{a}\), умноженным на число \(\lambda:\)

\(\bar{a}=\left(a_{1} ;\; a_{2} ;\; a_{3} \right)\Rightarrow \lambda \bar{a}=\left(\lambda a_{1} ;\; \lambda a_{2} ;\; \lambda a_{3} \right)\)

Особенность такого действия, как умножение вектора на число заключается в том, что число является простой численной формой величины, для которого отсутствует направление, а вектор определяется в качестве направленного отрезка, обладающего численным измерением и направлением.

Подобная операция, как и вычитание, нередко используется при решении задач в математике, геометрии и физике.

Произведение ненулевого вектора \(\vec{a}\) на число k является таким вектором \(\vec{b}\), длина которого составляет \(\left| \vec{b}\right|=\left|k \right|*\left|\vec{a} \right|\). При этом векторы \(\vec{a}\) и \(\vec{b}\) сонаправлены, если k больше или равно нулю, и противоположно направлены, когда k меньше нуля. Произведение нулевого вектора на любое число в результате позволяет получить ненулевой вектор.

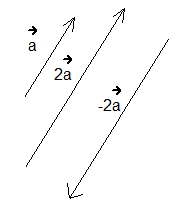
Предположим, что существует некий вектор \(\vec{a}\). В таком случае вектор \(\vec{2a}\) является вектором, направленным в ту же сторону, но с длиной, которая в 2 раза превышает длину вектора \(\vec{a}\). Длина его в два раза больше. Вектор \(\vec{-2a}\) является вектором, который направлен противоположно вектору \(\vec{a}\) и длиннее его в 2 раза.

Геометрическая и алгебраическая интерпретация умножения

Алгебраическая интерпретация: произведение ненулевого вектора на число представляет собой вектор с координатами, равными соответствующим координатам данного вектора, умноженным на число.

Яркий пример умножения вектора на число является второй закон Ньютона, который часто применяют при решении задач в физике. Если умножить обе части закона Ньютона на массу тела, то формула примет следующий вид:

\(m*\vec{a}=\vec{F}\)

После того, как умножили массу данного тела в виде скаляра m на ускорение тела, выраженного вектором \(\vec{a}\), в результате получили вектор \(m*\vec{a}\). Данный вектор можно обозначить, как \(\vec{F}\), который будет называться силой. Таким образом, под действием силы тело приобретает ускорение.

Рассматриваемая формула записана в векторном виде:

\(m*\vec{a}=\vec{F}\)

В таком случае говорят не только о модулях, то есть длинах векторов. С помощью векторного вида можно определить направление вектора. Согласно рассмотренному ранее определению произведения вектора на число, результат подобной операции не влияет на направление вектора. Его нельзя повернуть на какой-либо угол путем умножения на число. Результат произведения отличается лишь длиной вектора. Таким образом, векторы \(\vec{a}\) и \(\vec{F}\) характеризуются одинаковым направлением, но отличается по длине. В данном случае длина векторов отличается в m раз.

Понятие, основные свойства

В том случае, когда вектор \(\vec{b}\) равен произведению ненулевого числа k и ненулевого вектора \(\vec{a}\), то есть \(\vec{b}=k*\vec{a}\), справедливы следующие утверждения:

• \(\vec{a}\parallel\vec{b}\), то есть рассматриваемые вектора параллельны;
• \(\vec{a}\) и \(\vec{b}\) обладают одинаковым направлением при k больше нуля;
• \(\vec{a}\) и \(\vec{b}\) обладают разными направлениями при k меньше нуля.

Вектор можно умножить на число в виде скалярной величины. При этом в результате получится тоже вектор. После операции умножения длина заданного вектора изменится:

• длина вектора будет увеличена при умножении на число, модуль которого больше 1;
• длина вектора уменьшится в том случае, когда модуль числа меньше 1.

Если вектор умножить на положительное число, полученный вектор будет обладать таким же направлением, что и первоначальный. В том случае, когда предполагается произведение вектора на отрицательное число, полученный в результате вектор будет направлен в противоположную сторону.

В том случае, когда есть информация о координатах вектора, при умножении его на число следует умножить каждую координату рассматриваемого вектора на данное число.

\(\vec{a}=\left\{a_{x};a_{y} \right\}\)

Данная запись представляет собой координаты вектора \(\vec{a}.\)

\(k*\vec{a}=\left\{k*a_{x};k*a_{y} \right\}\)

Формулы применяющиеся при перемножении вектора и числа

В случае умножения вектора на число удобно использовать формулу умножения, предназначенную для решения плоских задач. При этом произведение вектора \(\vec{a}=\left\{a_{x};a_{y} \right\}\) и какого-то числа k вычисляют по формуле:

\(k*\vec{a}=\left\{k*a_{x};k*a_{y} \right\}\)

Если предполагается решить задачу пространственного типа на произведение вектора \(\vec{a}=\left\{a_{x};a_{y}; a_{z} \right\}\) и числа, то целесообразно воспользоваться следующей закономерностью:

\(k*\vec{a}=\left\{k*a_{x};k*a_{y}; k*a_{z} \right\}\)

Предусмотрена формула умножения n-мерного вектора. Когда n-мерный вектор \(\vec{a}=\left\{a_{1};a_{2};…; a_{n} \right\}\) умножают на число k, целесообразно воспользоваться формулой:

\(k*\vec{a}=\left\{k*a_{1};k*a_{2};…; k*a_{n} \right\}\)

Примеры задач с решением 

Задача 1

Дан вектор \(\vec{a}=\left\{1;2 \right\}\). Необходимо найти произведение этого вектора на 3.

Решение

В данном случае целесообразно воспользоваться формулой для решения плоских задач:

\(k*\vec{a}=\left\{k*a_{x};k*a_{y} \right\}\)

Таким образом:

\(3*\vec{a}=\left\{3*1;3*2 \right\}=\left\{3;6 \right\}\)

Ответ: \(\left\{3;6 \right\}\)

Задача 2

Задан пространственный вектор \(\vec{a}=\left\{1;2;-5 \right\}\). Данный вектор необходимо умножить на число -2.

Решение

В случае пространственной задачи следует воспользоваться следующей формулой:

\(k*\vec{a}=\left\{k*a_{x};k*a_{y}; k*a_{z} \right\}\)

Подставив числовые значения, получим:

\((-2)*\vec{a}=\left\{(-2)*1;(-2)*2; (-2)*(-5) \right\}=\left\{-2;-4;10 \right\}\)

Ответ: \(\left\{-2;-4;10 \right\}\)

Задача 3

Существует некий вектор \(\bar{a}=\left(-1;\; 2;\; 3\right)\). Требуется найти произведение этого вектора на число 2.

Решение

Исходя из определения, для умножения заданного вектора на число \(\lambda =2\) требуется каждую координату вектора \(\bar{a}\) умножить на это число. Таким образом:

\(2\bar{a}=2\cdot \left(-1;\; 2;\; 3\right)=\left(2\cdot \left(-1\right);\; 2\cdot 2;\; 2\cdot 3\right)=\left(-2;\; 4;\; 6\right)\)

Ответ: \(2\cdot \bar{a}=\left(-2;\; 4;\; 6\right)\)

Задача 4

Задан вектор \(\bar{a}=\left(-2;\; 4\right)\). Необходимо определить вектор \(-3\bar{a}\).

Решение

В том случае, когда требуется найти искомое произведение, следует умножить каждую координату заданного вектора \(\bar{a}\) на число \(\lambda =-3\). В результате умножения вектора на число получим:

\(-3\bar{a}=-3\cdot \left(-2;\; 4\right)=\left(-3\cdot \left(-2\right);\; -3\cdot 4\right)=\left(6;\; -12\right)\)

Ответ: \(-3\bar{a}=\left(6;\; -12\right)\)

Задача 5

Согласно анализу рассмотренных закономерностей, действия с векторами аналогичны действиям с алгебраическими выражениями. По этому принципу требуется упростить следующую запись:

\(\vec{p}=2(\vec{a}-\vec{b})+(\vec{c}+\vec{a})-3(\vec{b}-\vec{c}+\vec{a})\)

Решение

В первую очередь следует раскрыть скобки:

\(\vec{p}=2\vec{a}-2\vec{b}+\vec{c}+\vec{a}-3\vec{b}+3\vec{c}-3\vec{a}\)

Далее необходимо привести подобные:

\(\vec{p}=2\vec{a}+\vec{a}-3\vec{a}-2\vec{b}-3\vec{b}+\vec{c}+3\vec{c}=-5\vec{b}+4\vec{c}\)

Ответ: \(-5\vec{b}+4\vec{c}\)

Задача 6

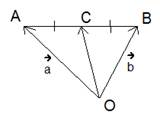
Имеется некий отрезок АВ. Точка С является серединой данного отрезка, точка О представляет собой произвольную точку плоскости. Также \(\vec{OA}=\vec{a}\) и \(\vec{OB}=\vec{b}.\) Требуется доказать, что:

\(\vec{OC}=1/2(\vec{a}+\vec{b})\)

Решение 1

Используя правило треугольника, можно выразить вектор \(\vec{OC}\) в виде суммы двух векторов:

\(\vec{OC}=\vec{a}+\vec{AC}\)

Кроме того, следует отметить, что:

\(\vec{OC}=\vec{b}+\vec{BC}\)

В результате получилась система двух уравнений:

\(\vec{OC}=\vec{a}+\vec{AC}\)

\(\vec{OC}=\vec{b}+\vec{BC}\)

Далее необходимо сложить уравнения системы:

\(2\vec{OC}=\vec{a}+\vec{AC}+\vec{b}+\vec{BC}=\vec{a}+\vec{b}+\vec{AC}+\vec{BC}\)

\(\vec{AC}+\vec{BC}=\vec{0}\)

Исходя из того, что С является серединой АВ, следует вывод: модули данных векторов равны, но они обладают разными направлениями. Таким образом, сумма векторов является нулевым вектором. В результате:

\(2\vec{OC}=\vec{a}+\vec{b}\)

При делении обеих частей уравнения на 2 получим:

\(\vec{OC}=1/2(\vec{a}+\vec{b})\)

Уравнение доказано.

Решение 2

\(\vec{OC}=\vec{a}+\vec{AC}=\vec{a}+1/2\vec{AB}=\vec{a}+1/2(\vec{b}-\vec{a})\)

Следует раскрыть скобки и привести подобные:

\(\vec{OC}=\vec{a}+1/2\vec{b}-1/2\vec{a}=\vec{a}-1/2\vec{a}+1/2\vec{b}=1/2(\vec{a}+\vec{b})\)

Уравнение доказано.

Задача 7

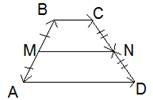
Требуется доказать, что средняя линия трапеции и ее основания параллельны друг другу, а также средняя линия трапеции равна половине суммы оснований.

Решение

Известно, что средней линией трапеции соединены ее боковые стороны. Основания трапеции параллельны друг другу. Согласно правилу многоугольника, можно выразить вектор \vec{MN} как сумму векторов:

\(\vec{MN}=\vec{MB}+\vec{BC}+\vec{CN}\)

С другой стороны:

\(\vec{MN}=\vec{MA}+\vec{AD}+\vec{DN}\)

В результате получена система уравнений:

\(\vec{MN}=\vec{MB}+\vec{BC}+\vec{CN}\)

\(\vec{MN}=\vec{MA}+\vec{AD}+\vec{DN}\)

Следует сложить уравнения системы:

\(2\vec{MN}=\vec{MB}+\vec{BC}+\vec{CN}+\vec{MA}+\vec{AD}+\vec{DN}=\vec{MB}+\vec{MA}+\vec{BC}+ \vec{AD}+\vec{CN}+\vec{DN}\)

Векторы \(\vec{MB}\) и \(\vec{MA}\) обладают противоположными направлениями и в сумме дают нулевой вектор, так как М — середина АВ, то есть модули данных векторов равны, кроме того, они противонаправлены. Аналогично векторы \(\vec{CN}\) и \(\vec{DN}\) дают в сумме нулевой вектор. Таким образом, получаем:

\(2\vec{MN}=\vec{BC}+\vec{AD}\)

Затем можно поделить обе части уравнения на 2:

\(\vec{MN}=1/2(\vec{BC}+\vec{AD})\)

В результате получено доказательство того, что средняя линия равна половине суммы оснований. Кроме того, прямая MN параллельна основаниям трапеции.