Произведение векторов друг на друга

Что такое произведение векторов

Это одна из основных операций над векторами в векторной алгебре. Вектор, в отличие от обычного отрезка, имеет не только длину, но и направление в пространстве.

Основные типы перемножения векторов

В математике есть два основных вида умножения векторов: скалярное и векторное. Результатом первого является число, результатом второго — вектор. Оба произведения применяются к двум векторам. Также выделяют смешанное произведение векторов, которое является комбинацией двух вышеописанных. Оно применяется, когда необходимо узнать результат умножения трех векторов.

Скалярное

Записывается скалярное произведение двумя способами: \( (\overline a,\;\overline b) \) или \( \overline a\cdot\overline b.\)

Алгебраические свойства скалярного произведения

1. Перестановочность. Произведение не меняется от перемены мест множителей: \(\overline a\cdot\overline b=\overline b\cdot\overline a.\)
2. Сочетательность относительно числа. Умножение одного из векторов на число равносильно умножению обоих векторов на это число: \((\lambda\overline a)\cdot\overline b=\lambda(\overline a\cdot\overline b)(\lambda\overline a)\cdot(\mu\overline b)=(\lambda\mu)(\overline a\cdot\overline b).\)
3. Распределительный закон. Скалярное произведение суммы двух векторов на третий равносильно сумме скалярных произведений этих векторов на третий вектор: \((\overline a+\overline b)\cdot\overline c=\overline a\cdot\overline c+\overline b\cdot\overline c.\)

Геометрические свойства скалярного умножения

1. Скалярное произведение вектора на него же равняется квадрату его модуля: \(\overline a\cdot\overline a=\overline a^2=\overline{\left|a\right|}\cdot\overline{\left|a\right|}\cdot\cos\left(0\right)=\left|\overline a^2\right|.\)
2. Если угол между векторами острый (меньше \(90^\circ\)), то скалярное произведение этих векторов больше нуля.
3. Если угол между векторами тупой (больше \(90^\circ\)), то их скалярное произведение меньше нуля.
4. Если вектора перпендикулярны (угол равен \(90^\circ\)), то их скалярное произведение будет равняться нулю.
5. Если координаты перемножаемых векторов известны, то их скалярное произведение будет равняться сумме произведений соответствующих координат:\( \overline a\cdot\overline b=a_x\cdot b_x+a_y\cdot b_y+a_z\cdot b_z.\)

Геометрический смысл

Скалярное произведение двух векторов равно произведению модуля одного из них на проекцию второго вектора на первый.

\(\overline a\cdot\overline b=\left|\overline a\right|\cdot пр_\overline a\overline b=\overline{\left|b\right|}\cdot пр_\overline b\overline a\)

\(пр_\overline b\overline a=\frac{\overline a\cdot\overline b}{\left|\overline b\right|}\)

Физический смысл

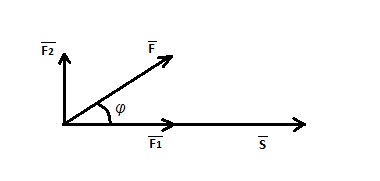
Скалярное произведение применяется для расчета работы, выполняемой при перемещении материальной точки вдоль вектора \(\overline s\) под действием силы \(\overline F\), приложенной под некоторым углом \(\varphi.\)

Рисунок 1. Физический смысл скалярного произведения

Силу \(\overline F\) необходимо разложить на ортогональные компоненты \(\overline{F_1}\) и \(\overline{F_2}.\) Тогда \(\overline{F_1}\) будет являться проекцией силы \(\overline F\) на вектор \(\overline s:\)

\(\left|\overline{F_1}\right|=\left|\overline F\right|\cdot\cos\left(\varphi\right).\)

В свою очередь, работа A вычисляется по формуле:

\(A=\left|\overline{F_1}\right|\cdot\left|\overline S\right|.\)

Соединив данные формулы получим:

\(A=\left|\overline F\right|\cdot\left|\overline S\right|\cdot\cos\left(\varphi\right),\)

что является скалярным произведением векторов \(\overline F\) и \(\overline s:\)

\(A=\overline F\cdot\overline S.\)

Векторное

Упорядоченная тройка некомпланарных векторов называется правой, если с конца третьего вектора кратчайший поворот от первого ко второму совершается против часовой стрелки. В противном случае такая тройка называется левой.

Три вектора называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях.

Векторное произведение может выражаться в записи двумя способами: \(\overline a\times\overline b\) и \(\lbrack\overline a,\overline b\rbrack.\)

Алгебраические свойства

1. Антиперестановочность. В отличие от скалярного произведения, в векторном при перемене мест множителей знак меняется на противоположный: \(\overline a\times\overline b=-(\overline b\times\overline a)\)
2. Сочетательность относительно числа. Как и в случае со скалярным умножением, произведение числа на один из векторов равняется произведению его на другой или на оба вектора: \((\lambda\overline a)\times\overline b=\overline a\times(\lambda\overline b)=\lambda(\overline a\times\overline b).\)
3. Распределительный закон. Векторное произведение суммы двух векторов на третий равносильно сумме векторных произведений этих векторов на третий вектор: \((\overline a+\overline b)\times\overline c=\overline a\times\overline c+\overline b\times\overline c.\)

Из этого следует, что при выполнении алгебраических действий, связанных с векторным произведением, скобки можно раскрывать так же, как при работе с числами, с поправкой на правило антиперестановочности.

Геометрические свойства

1. Если вектора \(\overline a\) и \(\overline b\) параллельны, то их векторное произведение равняется нулю.
2. Векторное произведение векторов с известными координатами выражается в матричном виде: \(\overline a\times\overline b=\begin{vmatrix}i&j&k\\a_x&a_y&a_z\\b_x&b_y&b_z\end{vmatrix}=\left(\begin{vmatrix}a_y&a_z\\b_y&b_z\end{vmatrix};\;-\begin{vmatrix}a_x&a_z\\b_x&b_z\end{vmatrix};\;\begin{vmatrix}a_x&a_y\\b_x&b_y\end{vmatrix}\right).\)

Геометрический смысл

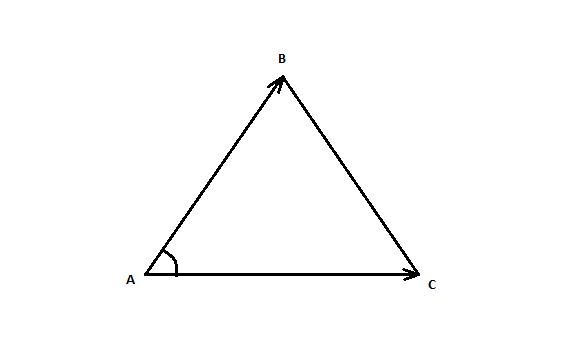
Модуль векторного произведения двух векторов равняется площади параллелограмма, сторонами которого являются эти вектора.

Рисунок 2. Геометрический смысл векторного произведения

Из определения векторного умножения следует, что модуль полученного вектора равняется произведению модулей исходных векторов на синус угла между ними:

\(\left|\overline c\right|=\left|\overline a\right|\cdot\left|\overline b\right|\cdot\sin\left(\varphi\right)\)

Площадь параллелограмма вычисляется так:

\(S=\left|\overline a\right|\cdot h, где h=\left|\overline b\right|\cdot\sin\left(\varphi\right).\)

Таким образом, получаем:

\(S=\left|\overline a\right|\cdot\left|\overline b\right|\cdot\sin\left(\varphi\right)=\left|\overline a\times\overline b\right|\)

Отсюда следует формула для площади треугольника:

\(S_\bigtriangleup=\frac12\left|\overline a\times\overline b\right|\)

Физический смысл

В физике векторное произведение применяется для расчета момента силы, приложенной к одной точке относительно другой:

\(\overline M=\overline{AB}\times\overline F\)

Смешанное умножение векторов

Фактически, смешанное произведение векторов представляется как скалярное умножение одного вектора на векторное произведение двух других. Результатом смешанного произведения является число.

Свойства смешанного умножения

1. \((\overline a\times\overline b)\cdot\overline c=\overline a\cdot(\overline b\times\overline c)=\overline a\cdot\overline b\cdot\overline c.\)
2. Если \(\overline a\cdot\overline b\cdot\overline c\) больше нуля, тройка векторов — правая.
3. Если\( \overline a\cdot\overline b\cdot\overline c\) меньше нуля, тройка векторов — левая.
4. Если вектора \(\overline a, \overline b\) и \(\overline c\) компланарны, то их смешанное произведение равняется нулю.

Геометрический смысл

Если вектора \overline a, \overline b и \overline c не компланарны, то их смешанное произведение равно объему параллелепипеда, построенного на этих векторах. Число будет положительным, если тройка векторов правая, и отрицательным, если тройка левая.

\(V_{пар.}=\overline a\cdot\overline b\cdot\overline c\)

Следствием этого является формула нахождения объема пирамиды:

\(V_{пир.}=\frac16\left(\overline a\cdot\overline b\cdot\overline c\right)\)

Произведение векторов, примеры и решения

Задача №1

Даны вектора \(\overline a=(-1,\;0,\;3) и \overline b=(2,\;-3,\;1).\)

Найти их скалярное произведение.

Решение

Возьмем формулу скалярного произведения для векторов с известными координатами:

\(\overline a\cdot\overline b=a_x\cdot b_x+a_y\cdot b_y+a_z\cdot b_z\) и подставим имеющиеся значения:

\(\overline a\cdot\overline b=(-1)\cdot2+0\cdot(-3)+3\cdot1=1\)

Задача №2

Найти площадь треугольника с известными координатами угловых точек

Координаты точек: \(A(-1,\;2,\;3), B(0,\;-2,\;1), C(1,\;2,\;1)\)

Решение

Для решения этой простейшей задачи из геометрии воспользуемся следствием геометрического смысла векторного произведения:

\(S_\bigtriangleup=\frac12\left|\overline a\times\overline b\right|\)

В данном случае треугольник построен на векторах\( \overline{AB}\) и \(\overline{AC}\). Чтобы рассчитать их координаты, необходимо вычесть из координат конечной точки координаты начальной:

\(\overline{AB}=(0-(-1),\;(-2)-2,\;1-3)=(1,\;-4,\;-2)\)

\(\overline{AC}=(1-(-1),\;2-2,\;1-3)=(2,\;0,\;-2)\)

Векторное произведение векторов с известными координатами выполняется в матричном виде:

\(\overline a\times\overline b=\begin{vmatrix}i&j&k\\a_x&a_y&a_z\\b_x&b_y&b_z\end{vmatrix}=\left(\begin{vmatrix}a_y&a_z\\b_y&b_z\end{vmatrix};\;-\begin{vmatrix}a_x&a_z\\b_x&b_z\end{vmatrix};\;\begin{vmatrix}a_x&a_y\\b_x&b_y\end{vmatrix}\right)\)

Подставляем значения векторов\( \overline{AB}\) и \(\overline{AC}\) в матрицу и производим вычисления:

\(\overline{AB}\times\overline{AC}=\begin{vmatrix}i&j&k\\1&-4&-2\\2&0&-2\end{vmatrix}=\left(i\begin{vmatrix}-4&-2\\0&-2\end{vmatrix};\;-j\begin{vmatrix}1&-2\\2&-2\end{vmatrix};\;k\begin{vmatrix}1&-4\\2&0\end{vmatrix}\right)=8i-2j+8k\)

Подставляем полученное значение в формулу вычисления площади треугольника, учитывая, что в ней фигурирует модуль произведения:

\(S_\bigtriangleup=\frac12\left|\overline{AB}\times\overline{AC}\right|=\frac12\sqrt{8^2+{(-2)}^2+8^2}=\sqrt{132}=11.49\)