Решение уравнений четвертой степени

Что относят к уравнениям четвертой степени, график

Рассматриваемые алгебраические соотношения относят к самой высокой категории, для которой применим способ вычисления в радикалах в обобщенном формате, то есть коэффициенты при этом могут иметь какое-либо значение без ограничений. Таким образом, образованная записанным выражением функция представляет собой многочлен 4 степени. Для нее характерен одинаковый предел в процессе продвижения от отрицательной к положительной бесконечности.

В том случае, когда а имеет значение больше нуля, можно наблюдать рост функции до положительной бесконечности с каждой из ее сторон. Исходя из этого, допустимо сформулировать вывод о наличии глобального минимума для этой функции. Таким же способом целесообразно рассмотреть ситуацию, при которой а меньше про сравнению с нулем. Тогда функция является убывающей в пространстве до отрицательной бесконечности с каждой из сторон, то есть обладает глобальным максимальным значением.

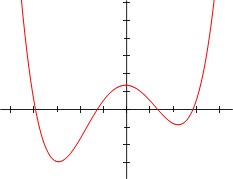
Изучить расположение и характер поведения функции можно с помощью наглядной схемы:

 

Источник: ru.wikipedia.org

Как решать

Существует несколько способов поиска корней, записи в упрощенном виде, доказательства справедливости уравнений в степени четыре. Знание таких методик позволит существенно сократить расчеты. Важно следовать стандартному алгоритму и внимательно относиться к преобразованию громоздких соотношений, особенно, в процессе раскрытия скобок.

Метод Феррари: формула

Предположим, что в качестве примера для выполнения решения представлено следующее алгебраическое выражение:

\(x^{4}+ax^{3}+bx^{2}+cx+d=0\)

Данное уравнение можно решить, прибегая к методике Феррари. С этой целью примем за  \(y_1\) какой-либо из корней записанного ниже уравнения 3 степени:

\(y^{3}-by^{2}+(ac-4d)y-a^{2}d+4bd-c^{2}=0\)

Таким образом, две пары решений начального выражения допустимо вычислить с помощью алгоритма, аналогичного схеме вычисления ответа для пары уравнений второй степени, а именно:

\(x^{2}+{\frac {a}{2}}x+{\frac {y_{1}}{2}}=\pm {\sqrt {\left({\frac {a^{2}}{4}}-b+y_{1}\right)x^{2}+\left({\frac {a}{2}}y_{1}-c\right)x+{\frac {y_{1}^{2}}{4}}-d}}\)

В данном примере запись, расположенная под знаком корня с правой стороны, представляет собой полный квадрат.

Теорема Виетта

Согласно закономерности Виетта, корни уравнения, имеющего формат 4 степени, а именно: \(x_{1}, x_{2},x_{3}, x_{4}\); объединены связью со следующими коэффициентами a, b, c, d, e, которую допустимо описать с помощью такого алгебраического соотношения:

\(x_{1}+x_{2}+x_{3}+x_{4}=-{\frac {b}{a}}\),

\(x_{1} x_{2}+x_{1} x_{3}+x_{1} x_{4}+x_{2} x_ {3}+x_{2} x_{4}+x_{3} x_{4}={\frac {c}{a}},\)

\(x_{1} x_{2} x_{3}+x_{1} x_{2} x_{4}+x_{1} x_{3} x_{4}+x_{2} x_{3} x_{4}=-{\frac {d}{a}},\)

\(x_{1} x_{2} x_{3} x_{4}={\frac {e}{a}}.\)

Примеры решения задач

Решение

Проанализируем условия задания. В данном случае целесообразно воспользоваться методом Феррари, чтобы вычислить искомые значения неизвестной х. Введем необходимые обозначения:

p=0,

q=4

r=-1

При этом резольвента Феррари примет следующий вид:

\(t^3+4t-16=0\)

Можно посчитать, чему соответствует корень крайнего записанного уравнения. Получим, что:

\(t_1=2\)

Таким образом, допустимо преобразовать начальное алгебраическое соотношение в следующий вид:

\((x^2+1)^2 =\left(\sqrt{2}x- \sqrt{2}\right)^2.\)

Заметим, что записанное выражение целесообразно представить в виде пары соотношений во второй степени, а именно:

\(x^2+1=\sqrt{2} x- \sqrt{2} u x^2+1=-\sqrt{2}x + \sqrt{2} .\)

Ответ: \(\frac{1\pm \mathbf i\sqrt{\sqrt{8}+1 }}{\sqrt{2}}, \frac{-1\pm \sqrt{\sqrt{8}-1 }}{\sqrt{2}}.\)

Решение

Здесь лучше начать решение с раскрытия скобок.

\((x^2-3x)(x^2-3x+2)=24\)

Внимательно изучим полученную математическую запись. Заметим, что в достаточно сложном многочлене допустимо выделить явную переменную. Запишем ее таким образом:

\(y=x^2-3x\)

Далее методом подстановки выполним необходимые преобразования и определим решение:

\(y \cdot (y+2)=24\)

\(y^2+2y-24=0\)

\(y_1=4;y_2=-6\)

В конце остается лишь вычислить неизвестные в простых уравнениях 2 степени:

\(x^2-3x=-4\)

\(x^2-3x=-6\)

Получим, что во втором случае решения отсутствуют, а корни первого выражения соответствуют следующим значениям:

\(x_1{1,2}=4;-1\)

Ответ: \(x_1{1,2}=4;-1\), второе решений не имеет.