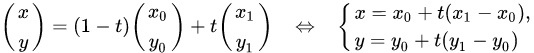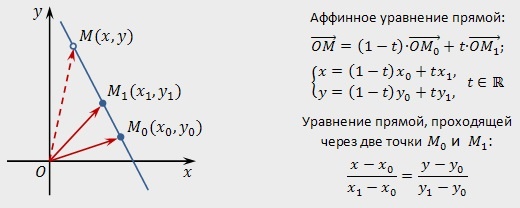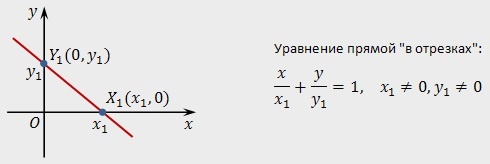Уравнение прямой, проходящей через 2 точки

Суть уравнения прямой, проходящей через две заданные точки

Можно представить, что на плоскости с координатами Oxy расположена пара точек: \(M_{0}(x_{0},y_{0})\), \(M_{1}(x_{1},y_{1})\)

Необходимо сделать вывод формулы для прямой, которая пересекает эти заданные точки.

Точка \(М (х, у)\) соответствует прямой \(M_{0} M_{1}\) только в том случае, когда ее радиус-вектор \(\vec{OM}\) соответствует следующему условию:

\(\vec{OM}=\left(1-t \right)\times \vec{OM_{0}}+t\times \vec{OM_{1}}\)

Где t является некоторым действительным числом (параметром). Координатная форма уравнения имеет следующий вид:

Данное равенство в алгебре называют аффинным уравнением прямой с пересечением двух точек в пространстве: \(M_{0}(x_{0},y_{0})\) и \(M_{1}(x_{1},y_{1})\).

Определив параметр t с помощью первого и второго уравнений системы, можно получить доказательство следующего соотношения:

\(\frac{x-x_{0}}{x_{1}-x_{0}}=t=\frac{y-y_{0}}{y_{1}-y_{0}}\)

Если исключить коэффициент t, то можно вывести уравнение прямой, проходящей через две точки: \(M_{0}(x_{0},y_{0})\) и \(M_{1}(x_{1},y_{1})\).

Формула будет иметь следующий вид:

\(\frac{x-x_{0}}{x_{1}-x_{0}}=\frac{y-y_{0}}{y_{1}-y_{0}}\)

Данное равенство вытекает из канонического уравнения, если выбрать направляющим вектором:

\(\vec{p}=a\vec{i}+b\vec{j}\)

Вектор \(\vec{M_{0}M_{1}}\) будет равен:

\(\vec{M_{0}M_{1}}=\left(x_{1}-x_{0} \right)\vec{i}+\left(y_{1}-y_{0} \right)\vec{j}\)

То есть, замещая следующие параметры:

\(a=x_{1}-x_{0}\)

\(b=y_{1}-y_{0}\)

Уравнение прямой в отрезках

Пусть координатные оси включают две точки: \(X_{1}\left(x_{1},0 \right)\) и \(Y_{1}\left(0, y_{1} \right)\)

Следует отметить следующее условие:

\(x_{1}\neq 0\)

\(y_{1}\neq 0\)

Необходимо записать уравнение прямой, которая проходит через заданные точки, подставив в формулу:

\(x_{0}=x_{1}\)

\(y_{0}=0\)

\(x_{1}=0\)

\(y_{1}=y_{1}\)

В результате уравнение принимает следующий вид:

\(\frac{x-x_{1}}{0-x_{1}}=\frac{y-0}{y_{1}-0}\Leftrightarrow -\frac{x}{x_{1}}+1=\frac{y}{y_{1}}\Leftrightarrow 1=\frac{x}{x_{1}}+\frac{y}{y_{1}}\)

Если поменять местами правую и левую части уравнения, то равенство примет такой вид:

\(\frac{x}{x_{1}}+\frac{y}{y_{1}}=1\)

\(x_{1}\neq 0\)

\(y_{1}\neq 0\)

Данную формулу называют уравнением прямой в отрезках. С помощью прямой, которая пересекает точки: \(X_{1}\left(x_{1},0 \right)\) и \(Y_{1}\left(0, y_{1} \right)\)

координатные оси делят на отрезки х₁ на оси абсцисс и у₁ на оси ординат. Длины отрезков будут рассчитаны следующим образом:

\(OX_{1}=\left|x_{1} \right|\)

\(OY_{1}=\left|y_{1} \right|\)

Как записать формулу, канонический вид

Какой-либо вектор, отличный от нуля, проходит по данной прямой или параллельно ей, называют направляющим вектором этой прямой. Для обозначения направляющего вектора произвольной прямой используют букву \(\bar{a}\)

Координаты данного вектора обозначают с помощью букв l, m, n. Таким образом, можно прийти к следующему уравнению:

\(\bar{a}=\left\{l; m; n \right\}\)

При известном значении одной точки \(M_{0}\left(x_{0};y_{0};z_{0} \right)\) и направляющего вектора \(\bar{a}=\left\{l; m; n \right\}\) прямой, то для нее будут записаны следующие уравнения:

\(\frac{x-x_{0}}{l}=\frac{y-y_{0}}{m}=\frac{z-z_{0}}{n}\)

Уравнение в таком виде называют каноническим.

Параметрическое уравнение прямой, проходящей через две точки

Канонические уравнения для прямой, которая пересекает следующие точки:

\(M_{1}\left(x_{1};y_{1};z_{1} \right)\)

\(M_{2}\left(x_{2};y_{2};z_{2} \right)\)

будет записано в следующем виде:

\(\frac{x-x_{1}}{x_{2}-x_{1}}=\frac{y-y_{1}}{y_{2}-y_{1}}=\frac{z-z_{1}}{z_{2}-z_{1}}\)

Равные отношения можно обозначить буквой t в канонических уравнениях. В итоге они приобретают такой вид:

\(\frac{x-x_{0}}{l}=\frac{y-y_{0}}{m}=\frac{z-z_{0}}{n}=t\)

Исход из этого, получается равенство:

\(x=x_{0}+lt\)

\(y=y_{0}+mt\)

\(z=z_{0}+nt\)

Данные равенства являются параметрическими уравнениями прямой, которая пересекает точку \(M_{0}\left(x_{0};y_{0}; z \right)\) в направлении вектора \(\bar{a}=\left\{l; m; n \right\}\)

В данном случае t является произвольно изменяющимся параметром, x, y, z представляют собой функции от t. Если изменяется t, то значения x, y, z также меняются. Таким образом, точка M (x; y; z) перемещается вдоль прямой. Если параметр t использовать в качестве переменного времени, а уравнения представить в виде формул, описывающих движение точки М, то с помощью данных уравнений можно определить прямолинейное и равномерное движение точки М. При t равным 0 точка М будет совпадать с точкой M₀.

Скорость V точки М обладает постоянным значением и рассчитывается по формуле:

\(V=\sqrt{l^{2}+m^{2}+n^{2}}\)

Примеры задач с решением

Задача 1

Необходимо построить прямую, которая проходит через следующие точки: А (2, 1, 1), В (3, 1, -2).

Решение

Уравнение прямой, которая проходит через точки:

\(A\left(x_{1},y_{1},z_{1} \right)\)

\(B\left(x_{2},y_{2},z_{2} \right)\)

будет иметь следующий вид:

\(\frac{x-x_{1}}{x_{2}-x_{1}}=\frac{y-y_{1}}{y_{2}-y_{1}}=\frac{z-z_{1}}{z_{2}-z_{1}}\)

После того, как координаты точек А и В будут применены к первому уравнению, оно будет записано в такой форме:

\(\frac{x-2}{3-2}=\frac{y-1}{1-1}=\frac{z-1}{-2-1}\)

После некоторых преобразований получается:

\(\frac{x-2}{1}=\frac{y-1}{0}=\frac{z-1}{-3}\)

В данном случае наличие ноля в знаменателе не обозначает деление на ноль. Параметрическое уравнение прямой будет записано таким образом:

\(t=\frac{x-2}{1}\)

\(t=\frac{ y-1}{0}\)

\(t=\frac{z-1}{-3}\)

Если выразить переменные x, y, z с помощью параметра t, в итоге получится:

\(x = t + 2\)

\(y = 1\)

\(z = -3 * t + 1\)

Ответ: каноническое уравнение прямой, проходящей через точки A(2, 1, 1), B(3, 1, -2), будет записано в следующем виде:

\(\frac{x-2}{1}=\frac{y-1}{0}=\frac{z-1}{-3}\)

Параметрическое уравнение прямой, проходящей через точки A(2, 1, 1), B(3, 1, -2), будет записано в следующем виде:

\(x = t + 2\)

\(y = 1\)

\(z = -3 * t + 1\)

Задача 2

Требуется построить прямую, которая проходит через точки А (1, 1/5, 1) и В (-2, 1/2, -2).

Решение

Уравнение для прямой, которая пересекает заданные точки:

\(A\left(x_{1},y_{1},z_{1} \right)\)

\(B\left(x_{2},y_{2},z_{2} \right)\)

будет записано таким образом:

\(\frac{x-x_{1}}{x_{2}-x_{1}}=\frac{y-y_{1}}{y_{2}-y_{1}}=\frac{z-z_{1}}{z_{2}-z_{1}}\)

После подстановки координат точек А и В в исходную формулу, она приобретет такой вид:

\(\frac{x-1}{-2-1}=\frac{y-\frac{1}{5}}{\frac{1}{2}-\frac{1}{5}}=\frac{z-1}{-2-1}\)

или

\(\frac{x-1}{-3}=\frac{y-\frac{1}{5}}{\frac{3}{10}}=\frac{z-1}{-3}\)

Далее можно записать параметрическое уравнение прямой:

\(t=\frac{x-1}{-3}\)

\(t=\frac{y-\frac{1}{5}}{\frac{3}{10}}\)

\(t=\frac{z-1}{-3}\)

Выразив переменные x, y, z с помощью параметра t, можно получить следующее уравнение:

\(x=-3\times t+1\)

\(y=\frac{3}{10}t+\frac{1}{5}\)

\(z=-3\times t+1\)

Ответ: каноническое уравнение прямой, пересекающей заданные точки A(1, 1/5, 1) и B(−2, 1/2, −2) записано в следующем виде:

\(\frac{x-1}{-3}=\frac{y-\frac{1}{5}}{\frac{3}{10}}=\frac{z-1}{-3}\)

параметрическое уравнение прямой, проходящей через точки A(1, 1/5, 1) и B(−2, 1/2, −2) имеет следующий вид:

\(x=-3\times t+1\)

\(y=\frac{3}{10}t+\frac{1}{5}\)

\(z=-3\times t+1\)