Решение уравнения касательной через график производной функции
Геометрический смысл производной функции в точке
Производная функции, имеющей вид f(x), в некой точк \(x_0\) является пределом отношения приращения функции \(\Delta f=f(x_0+\Delta x)-f(x_0)\) к приращению аргумента \(\Delta x\), если \(\Delta x\rightarrow 0\), и данный предел существует.
Вывод формулы имеет следующий вид:
\(f'(x_0)=\lim_{\Delta x\rightarrow 0}\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x}\)
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Графически производную можно изобразить в виде кривой таким образом:
Разберем типичный пример в доказательство определению. Попробуем найти производную записанным ранее методом \((x^2+1)\):
\((x^2+1)'=\lim_{\Delta x\rightarrow 0}\frac{((x+\Delta x)^2+1)-(x^2+1)}{\Delta x}=\lim_{\Delta x\rightarrow 0}\frac{x^2+2x\Delta x+\Delta x^2-x^2}{\Delta x}= \lim_{\Delta x\rightarrow 0}\frac{\Delta x(2x+\Delta x)}{\Delta x}=2x\)
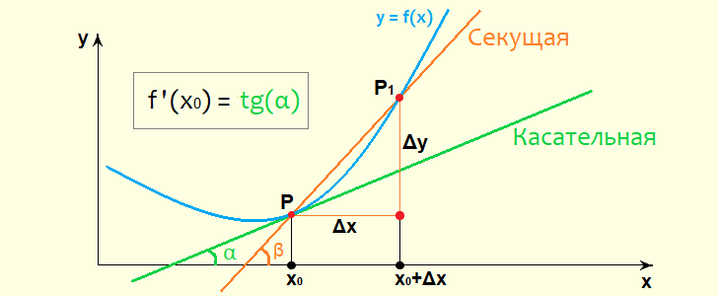
Согласно историческим фактам, одновременно с написанием работы Ньютона по изучению процессов в физике и формулировке понятия производной Лейбницем было введено определение производной с помощью геометрических закономерностей. Узнать, в чем состоит геометрический смысл производной, можно с помощью исследования графика функции y=f(x) на плоскости:
В качестве обозначения точки \(х0\), соответствующей значению заданной функции, используем Р. Затем построим некую секущую, которая будет пересекать точки Р и Р1. Предположим, что полученный угол, образованный положительным направлением оси абсцисс Х и построенной секущей, равен \(\beta\).
Результатом наших действий является геометрическая фигура под названием прямоугольный треугольник, катеты которого соответствуют переменным \(\triangle x\) и \(\triangle y\). Введем обозначения:
- \(\triangle x\) обозначает приращение аргумента функции;
- \(\triangle y \) является приращением функции непосредственно.
Приращение функции относится к приращению аргумента, как тангенс угла, образованный секущей и положительным направлением оси абсцисс:
\(\frac{\triangle x}{\triangle y}=tg \beta\)
Когда значение \(\triangle x\) стремится к нулю, точка Р1 на изображенном графике смещается в сторону точки Р. Положение секущей в таком случае меняется по отношению к графику.
Секущая занимает предельное положение в виде прямой, когда приращение стремится к нулю. Точки Р и Р1 на данной прямой будут совмещены. Рассматриваемая прямая является касательной к графику в точке Р.
Запишем следующее соотношение:
\(tg\beta \rightarrow tg\alpha, если \triangle x\rightarrow 0\)
Геометрический смысл производной: производная функции в точке обладает значением, численно равным тангенсу угла наклона касательной к функции в рассматриваемой точке.
Известным фактом является то, что какая-либо прямая обладает уравнением, которое можно записать в общем виде:
\(y=k \cdot x+b\)
В уравнении касательной к функции в некой точке Р коэффициент k определяется, как значение производной в точке х0:
\(\lim_{\triangle x \rightarrow 0}\frac{\triangle x}{\triangle y}=tg \alpha = k\)
В процессе решения практических заданий нередко можно встретить примеры, где требуется использовать геометрический смысл производной. Одной из подобных задач является изучение графически заданной функции в сравнении с графиком производной искомой функции.
Уравнение касательной к графику функций
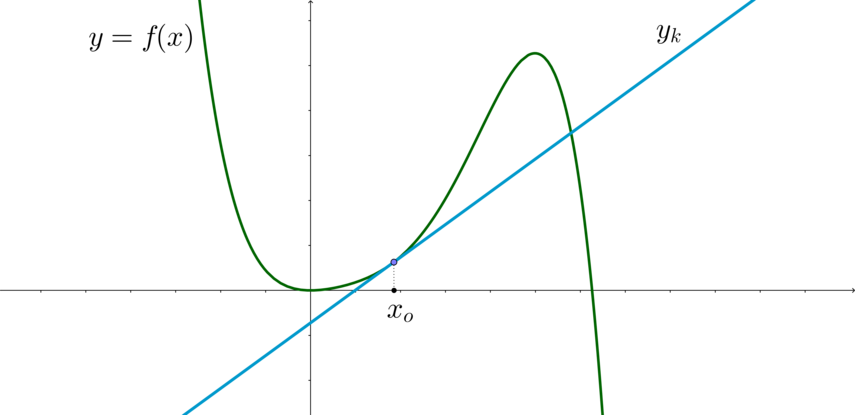
Представим, что имеется некая функция \(y=f(x)\). Отметим на ее графике точку \(x_o\). Если провести касательную, пересекающую данную точку, то ее можно задать с помощью следующего уравнения:
\(\Large{y_k=f(x_o)+f'(x_o)(x-x_o)}\)
В результате угловой коэффициент касательной будет определен по формуле:
\(k=f'(x_o)\)
В качестве наглядного примера изобразим график по исходным данным:
Определение таких значений для k и b, при которых прямая \(y_k=kx+b\) играет роль касательной к функции \(y=f(x)\), заключается в решении одной из следующих систем:
\(\Large{\begin{cases} k=f'(x_o)\\ b=f(x_o)-f'(x_o)\cdot x_o\end{cases}}\)
\(\Large{\begin{cases} k=f'(x_o)\\ f(x_o)=y_k(x_o)\end{cases}}\)
Алгоритм составления уравнения касательной к графику функции
Составить уравнение, с помощью которого задана касательная к графику функции, несложно. Нужно лишь следовать следующему алгоритму и выполнять действия в таком порядке:
- Рассчитать значение \( f\left( {{x}_{0}} \right).\)
- Записать формулу производной функции \({f}’\left( x \right).\)
- Определить значение \({f}’\left( {{x}_{0}} \right).\)
- Выполнить подстановку \({{x}_{0}},\text{ }f\left( {{x}_{0}} \right)\) и \({f}’\left( {{x}_{0}} \right) \)в формулу уравнения касательной \(y={f}’\left( {{x}_{0}} \right)\cdot \left( x-{{x}_{0}} \right)+f\left( {{x}_{0}} \right).\)
Рассмотрим конкретный пример. Попробуем составить уравнение касательной к функции \(f\left( x \right)={{x}^{2}}-2x+3.\) Выполним действия последовательно, руководствуясь записанным ранее алгоритмом:
\(f\left( x \right)={{x}^{2}}-2x+3, {{x}_{0}}=3\)
\(f\left( {{x}_{0}} \right)=f\left( 3 \right)={{3}^{2}}-2\cdot 3+3=6\)
\({f}’\left( x \right)={{\left( {{x}^{2}}-2x+3 \right)}^{\prime }}=2{x} -2\)
\({f}’\left( {{x}_{0}} \right)={f}’\left( 3 \right)=2\cdot 3-2=4\)
\(\begin{array}{l}y={f}’\left( {{x}_{0}} \right)\cdot \left( x-{{x}_{0}} \right)+f\left( {{x}_{0}} \right)=\\\text{ }=4\left( x-3 \right)+6=4{x} -12+6=4{x} -6\end{array}\)
Примеры решения задач
Функция \( y=\mathsf{f}\left( x \right)\) изображена графически. На этом же правильном графике построена касательная в точке, абсцисса которой равна \({x}_{0}.\)
Требуется определить значения производной функции \(\mathsf{f}\left( x \right)\), которые она принимает в точке \({{x}_{0}}.\)
Решение
Согласно определению значения производной в точке касания, запишем:
\(f’\left( x \right)=k=\ {tg}\varphi\)
Заметим, что для вычисления значения производной требуется определить тангенс угла наклона касательной. Воспользуемся координатами пары точек, которые принадлежат касательной на графике, чтобы построить прямоугольный треугольник. Угол наклона касательной к оси абсцисс равен \(\angle BAC\). Определим тангенс рассматриваемого угла:
\(\ {tg}\angle BAC=\frac{BC}{AC}=\frac{6}{5}=1,2.\)
В результате значение производной функции \(\mathsf{f}\left( x \right)\) в точке \({{x}_{0}}\) соответствует 1,2.
Ответ: 1,2.
Дана некая функция \(y=\frac{1}{3}x^3-4x+1\). Требуется записать уравнение касательной к графику этой функции в точке \(x_0=3.\)
Решение
\(f'(x)=x^2-4\)
\(f'(3)=3^2-4=5\)
\(f(3)=\frac{1}{3}\cdot 3^3-4\cdot 3+1=9-12+1=-2.\)
В таком случае:
\(y_k=f'(x_0)(x-x_0)+f(x_0)\)
\(y_k=5(x-3)-2\)
\(y_k=5x-17\)
Ответ: \(y=5x-17.\)
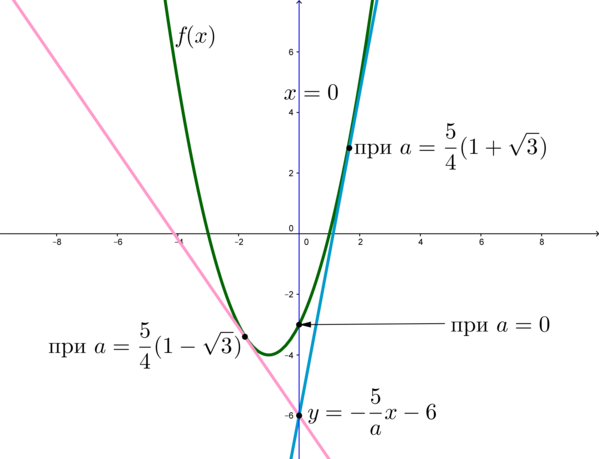
Изображено два графика функций:
\(f(x)=x^2+2x-3\)
\(ay+5x+6a=0\)
Нужно вычислить все значения, которые принимает параметр а при пересечении рассматриваемых графиков только в одной точке.
Решение
Функция \(f(x)\) на графике будет иметь вид параболы, пересекающей ось абсцисс в следующих точках:
x=-3
x=1
Данная парабола имеет одну точку пересечения с осью ординат:
y=-3
Если зафиксировать а, то при каждом таком значении \(ay+5x+6a=0\) будет иметь вид прямой:
- если a=0, то прямая x=0 с единственной точкой пересечения с f(x), соответствующей (0;-3);
- если \(a\ne 0,\) то получается пучок прямых \(y=-\dfrac{5}{a}x-6\), пересекающих точку (0;-6).
В результате графики обладают единственной общей точкой при таких значениях a, при которых прямая y будет касаться параболы. Касание в точке \(x_o\) возможно при следующих условиях:
\(\begin{cases} f'(x_o)=-\dfrac{5}{a}\\ f(x_o)=y(x_o) \end{cases} \Rightarrow \begin{cases} x_o=-\dfrac{5}{2a}-1\\ 8a^2-20a-25=0 \end{cases} \Rightarrow a=\dfrac{5}{4}(1 \pm \sqrt3)\)
Ответ: \(a\in \Big\{ \dfrac{5}{4}(1-\sqrt3); \ 0; \ \dfrac{5}{4}(1+\sqrt3)\Big\}.\)
Имеется некое уравнение:
\(\dfrac{1}{3}x^3+2x^2-\dfrac{88}{3}=a(x+8)\)
Требуется определить все вероятные значения, которыми обладает параметр а, определяющие для данного уравнения единственное решение.
Решение
Проанализируем функцию и пучок, состоящий из прямых:
\(f(x)=\dfrac{1}{3}x^3+2x^2-\dfrac{88}{3}\)
\(y=a(x+8)\)
Точка максимума равна:
\(f'(x)=x^2+4x \Rightarrow x=-4=x_{max}\)
Точка минимума равна:
\(x=0=x_{min}\)
Запишем следующие соотношения:
\(f(x_{max})=-\dfrac{56}{3}\)
\(f(x_{min})=-\dfrac{88}{3}\)
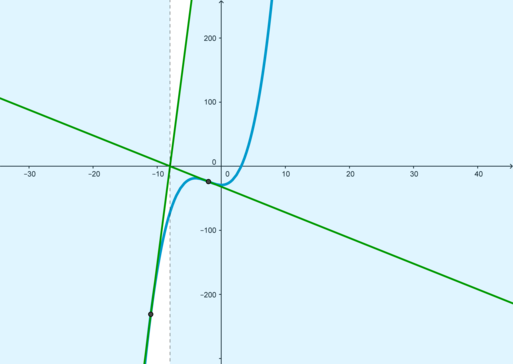
Каждая из прямых \(y=ax+8a\) пересекает точку (-8;0). Выявим такие случаи, при которых прямая у будет касаться графика функции f(x) в точке касания \(x_o.\) Подберем под заданные условия значения параметра:
\(\begin{cases} f'(x_o)=a\\ f(x_o)=y(x_o) \end{cases} \Rightarrow \begin{cases} x_o^2+4x_o=a\\ 2x_o^3+30x_o^2+96x_o+88=0 \end{cases}\Rightarrow \begin{cases} x_o^2+4x_o=a\\ (x_o+2)^2(x_o+11)=0 \end{cases} \Rightarrow \left[ \begin{gathered} \begin{aligned} &\begin{cases} x_o=-2\\ a=-4 \end{cases}\\ &\begin{cases} x_o=-11\\ a=77 \end{cases} \end{aligned} \end{gathered} \right.\)
В результате уравнение \( f(x)=y\) обладает только одним значением, когда параметр а имеет значения, при которых прямые y проходят в заштрихованных участках. Отметим, что граничный случай a=77 является посторонним.
График в уменьшенном масштабе:
Таким образом:
\(a\in (-\infty; 77)\)
Ответ: \(a\in (-\infty; 77).\)
Записана система:
\(\begin{cases} \sqrt{(x-a)^2+y^2}+\sqrt{x^2+(y+a)^2}=|a\sqrt2|\\ x^2+y^2\leqslant 18 \end{cases}\)
Нужно найти такие значения параметра а, при которых данная система обладает только одним решением.
Решение
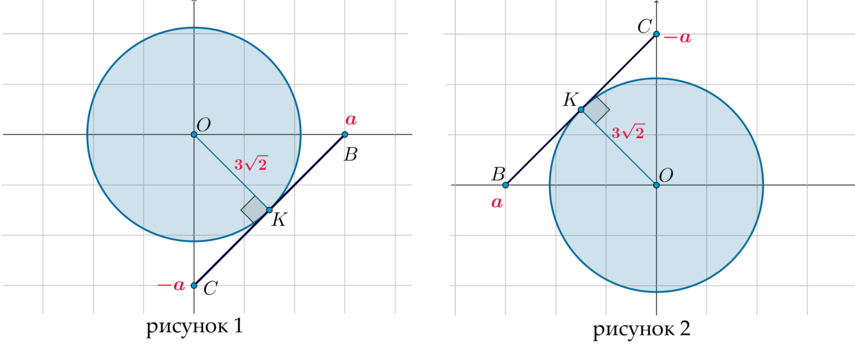
С помощью первого из уравнений системы можно построить отрезок BC, где B(a;0), C(0;-a), при условии, что a≠0. Представим, что \(A(x;y)\). В таком случае:
\(\begin{aligned} &BA=\sqrt{(x-a)^2+y^2}\\[1ex] &AC=\sqrt{x^2+(y+a)^2}\\[1ex] &BC=\sqrt{(a-0)^2+(0+a)^2}=|a\sqrt2| \end{aligned}\)
Запишем первое из уравнений, как:
BA+AC=BC
Заметим, с помощью этого уравнения можно задать множество точек А, принадлежащих отрезку ВС. Если а=0, то рассматриваемое уравнение задает только одну точку O(0;0).
С помощью второго неравенства можно изобразить окружность, центр которой находится в точке O(0;0), а ее радиус равен \(R=3\sqrt2.\)
Система будет иметь лишь одно решение при параметре а≠0 — в том случае, когда отрезок касается окружности:
- если a>0, отрезок BC располагается в 4 четверти;
- если a<0, отрезок ВС располагается во 2 четверти.
Вариант с нулевым значением (а=0) также подходит под условия задачи, так как точка О лежит на окружности.
Когда a>0, получим:
\(BO=CO=|a|=a\)
\(OK=3\sqrt2\), является радиусом, проведенным в точку касания.
В таком случае:
\(\dfrac12\cdot OB\cdot OC=S_{\triangle OBC}=\dfrac12\cdot OK\cdot BC \quad\Rightarrow\quad a\cdot a=3\sqrt2\cdot a\sqrt2 \quad\Rightarrow\quad a=6.\)
Когда a<0, получим:
\(BO=CO=|a|=-a\)
В таком случае:
\(\dfrac12\cdot OB\cdot OC=S_{\triangle OBC}=\dfrac12\cdot OK\cdot BC \quad\Rightarrow\quad -a\cdot (-a)=3\sqrt2\cdot (-a\sqrt2) \quad\Rightarrow\quad a=-6.\)
Ответ: \(a\in \{-6;0;6\}.\)
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так