Уравнение прямой, проходящей через центр окружности

Уравнение окружности и прямой — как между собой связаны

Записать уравнение окружности можно, используя известные свойства геометрической фигуры:

1. Любые точки окружности равноудалены от ее центра. Расстояние является радиусом.
2. Зная координаты точек, можно записать формулу для определения расстояния между ними: \(|AB|=\sqrt{(x_{A}−x_{B})^{2}+(y_{A}−y_{B})^{2}}\). Таким образом, квадрат расстояния равен \(AB^{2}=(x_{A}−x_{B})^{2}+(y_{A}−y_{B})\).

Уравнение для описания окружности, которая имеет радиус R, а ее центр совпадает с точкой \(O(x_0;y_0)\), имеет вид:

\((x-x_0)^2+(y-y_0)^2 = R^2\)

В том случае, когда центр окружности лежит в точке начала координат, уравнение окружности приобретает упрощенную форму:

\(x^2+y^2=R^2\)

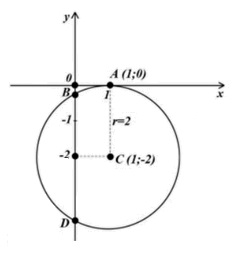
Предположим, что существует уравнение некой окружности:

\((x-1)^2+(y+2)^2=4\)

Центром данной геометрической фигуры является точка C(1;-2). Радиус окружности равен R=2.

Каждую прямую на плоскости можно представить в виде уравнения прямой первой степени. Формула имеет следующий вид:

Ax + By + C = 0

В данном случае А и В не могут одновременно принимать нулевые значения.

С учетом углового коэффициента общее уравнение прямой при значении b, не равном нулю, записывают следующим образом:

y = kx + b

Здесь k является угловым коэффициентом, который можно посчитать, как тангенс угла между рассматриваемой прямой и положительным направлением оси ОХ.

Рассмотрим случай, когда прямая пересекает оси ОХ и ОУ в точках, имеющих следующие координаты:

\((a; 0)\ и\ (0; b)\)

Найти рассматриваемую прямую можно с помощью уравнения прямой в отрезках:

\(\frac{x}{a}+\frac{y}{b}=1\)

Предположим, что прямая пересекает пару точек \(A(x_1;y_1)\) и \(B(x_2; y_2),\) удовлетворяющих данным условиям:

\(x_1 ≠ x_2\ и\ y_1 ≠ y_2\)

В таком случае уравнение прямой рассчитывают по формуле:

\(\frac{x-x_1}{x_2-x_1}=\frac{y-y_1}{y_2-y_1}\)

Например, существует некая прямая в прямоугольной системе координат. Данная прямая пересекает пару точек:

\(M_1(1;1)\) и \(M_2(4;2)\)

Уравнение прямой, проходящей через две обозначенные точки, имеет вид:

\(\frac{x-1}{4-1}=\frac{y-1}{2-1} \Leftrightarrow \frac{x-1}3=\frac{y-1}1\)

Преобразуем полученное уравнение:

\(\frac{x-1}3=\frac{y-1}1 \Leftrightarrow 1\cdot (x-1)=3\cdot(y-1) \Leftrightarrow x-3y+2=0\)

Как составить уравнение прямой, проходящей через центр окружности

Применяя записанные ранее уравнения для прямой и окружности, можно найти уравнение прямой, которая проходит через центр окружности:

\(x^2+y^2-6x-8y+16=0\)

\(x^2+y^2+10x+4y+13=0\)

В первую очередь следует рассчитать радиусы и определить координаты центров окружностей:

\(x^2 + y^2 - 6x - 8y + 16 = 0\)

\((x^2 - 6x + 9) + (y^2 - 8y + 16) = 9\)

\((x - 3)^2 + (y - 4)^2 = 3^2\)

\(r1 = 3\)

\(O_1(3;4)\)

\(x^2 + y^2 + 10x + 4y + 13 = 0\)

\((x^2 + 10x + 25) + (y^2 + 4y + 4) = 16\)

\((x + 5)^2 + (y + 2)^2 = 4^2\)

\(r2 = 4\)

\(O_2(-5;-2)\)

Уравнение прямой, проходящей через точки \(O_1(3;4)\) и \(O_2(-5;-2)\), можно записать следующим образом:

\(\frac{(x - 3)}{(3 + 5)}=\frac{(y - 4)}{(4 + 2)}\)

\(\frac{(x - 3)}{8}=\frac{(y - 4)}{6}\)

\(3(x - 3) = 4(y - 4)\)

\(3x - 9 = 4y - 16\)

\(4y = 3x + 7\)

\(y = \frac{3x}{4}+\frac{7}{4}\)

В результате уравнение прямой принимает такой вид:

\(y = \frac{3x}{4}+\frac{7}{4}\)

Решение задач по теме, примеры

Задача 1

Требуется определить, где находится центр окружности, и чему равен ее радиус. Уравнение окружности:

\(x^{2}+(y-3)^{2}=49\)

Необходимо представить график окружности в осях абсцисс и ординат.

Решение

Каноническое уравнение окружности имеет вид:

\((x-h)^{2}+(y-k)^{2}=r^{2}\)

В данном случае, центр соответствует О:(h, k), а радиус окружности равен r.

По условиям задачи: \(x^{2}+(y-3)^{2}=49\)

Таким образом:

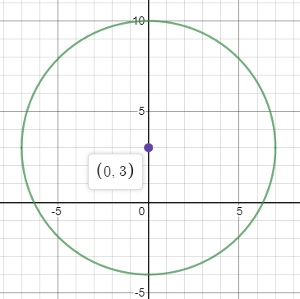
\(O:(0, 3)\qquad r=7\)

График:

Ответ: центр совпадает с точкой, имеющей координаты \((0, 3)\qquad r=7\)

Задача 2

Нужно определить, в какой точке расположен центр окружности, и чему равен ее радиус. Уравнение окружности:

\((x+2)^{2}+y^{2}=36\)

Решение

В первую очередь следует записать каноническое уравнение окружности:

\((x-h)^{2}+(y-k)^{2}=r^{2}\)

В данном случае, центр окружности совпадает с точкой, имеющей координаты (h, k), а ее радиус равен r.

Согласно условиям задачи:

\((x+2)^{2}+y^{2}=36\)

Таким образом:

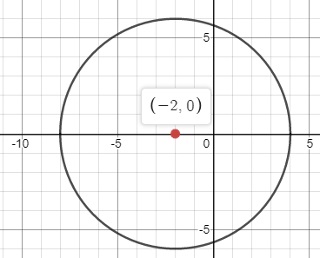
\(O:(-2, 0)\qquad r=6\)

График:

Ответ: центр окружности совпадает с точкой (-2, 0), а ее радиус равен 6.

Задача 3

Требуется преобразовать уравнение в сумму квадратов для расчета радиуса и определения центра окружности:

\(2x^{2}+2y^{2}+4x+16y+1=0\)

Решение

\(2x^{2}+2y^{2}+4x+16y+1=0\Longrightarrow x^{2}+y^{2}+2x+8y+\frac{1}{2}=0\)

В таком случае:

\(\left(x+1\right)^{2}+\left( y+4\right)^{2}-1-16+\frac{1}{2}=0\Longrightarrow \left(x+1\right) ^{2}+\left(y+4\right) ^{2}=\frac{33}{2}\)

В результате расчетов получим:

центр находится в (-1,-4)

радиус равен \(\sqrt{\frac{33}{2}}\)

Ответ: \(O (-1,-4)\ и\ r=\sqrt{\frac{33}{2}}\)

Задача 4

Центр окружности совпадает с точкой (4,-5). Необходимо записать уравнение данной окружности, учитывая, что она проходит через точку с координатами (7,-3).

Решение

Каноническое уравнение окружности:

\((x-h)^{2}+(y-k)^{2}=r^{2}\)

Центр находится в точке:

(4,-5)

Радиус соответствует r.

Таким образом:

\((x-4)^{2}+(y+5)^{2}=r^{2}\Longrightarrow r=\sqrt{(x-4)^{2}+(y+5)^{2}}\)

Учитывая, что окружность проходит через точку (7,-3), запишем:

\(r=\sqrt{\left(3\right)^{2}+\left(2\right)^{2}}=\sqrt{13}\)

Ответ: уравнение окружности имеет вид \((x-4)^{2}+(y+5)^{2}=13\)

Задача 5

Необходимо записать уравнение окружности, центр которой соответствует точке O(2,-1), касающейся прямой r:y=x+2. Требуется начертить график.

Решение

Зная, что радиус r является расстоянием, на которое удалены точка O:(h, k) и прямая y-x-2=0, запишем:

\(O:(2,-1)\)

\(r=d(O,L)=\frac{\left\vert -2-1-2\right\vert }{\sqrt{1^{2}+\left( -1\right) ^{2}}}=\frac{5}{\sqrt{2}}\)

Получим уравнение окружности:

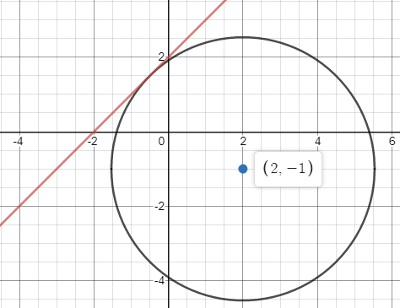
\((x-h)^{2}+(y-k)^{2}=r^{2}\Longrightarrow (x-2)^{2}+(y+1)^{2}=\frac{25}{2}\)

График:

Ответ: \((x-2)^{2}+(y+1)^{2}=\frac{9}{5}\)

Задача 6

Требуется записать уравнение, описывающее прямую с угловым коэффициентом \(k= \frac{3}{2}\). Искомая прямая пересекает точку А (3;2).

Решение

В первую очередь следует записать стандартную формулу:

\(y-y_{0}=k(x-x_{0})\)

Применительно к условиям задачи, получим:

\(y-(-2)= \frac{3}{2} (x-3)\)

\(y+2= \frac{3}{2}х-\frac{9}{2}\)

\(y= \frac{3}{2}х-\frac{13}{2}\)

Ответ: \(y= \frac{3}{2}х-\frac{13}{2}\)