Вектор индукции магнитного поля
Магнитное поле и вектор магнитной индукции: определение
Магнитное поле возникает вокруг постоянных электрических токов и постоянных магнитов.
Постоянный ток — электрический ток, который со времени не изменяется по величине и направлению.
Постоянный магнит — магнит, который в течение очень долгого времени не теряет магнитные свойства.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Для регистрации магнитного поля в виде пробного тела используется электрический заряд, причем пробным телом для него могут являться стрелка компаса, элемент тока или рамка с током площадью S.
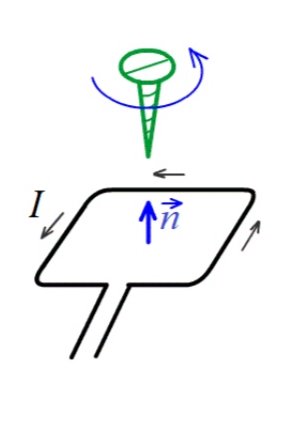
Определим положение рамки с током в пространстве с помощью вектора нормали к плоскости рамки с учетом того, что ток течет против часовой стрелки.
Вектор нормали к плоскости — любой ненулевой вектор, принадлежащий прямой, которая перпендикулярна к рассматриваемой плоскости.
В данном случае в качестве вектора нормали выступает вектор n.
Используем правило правой руки: ладонь обхватывает проводник, и большой палец правой руки показывает направление тока. В таком случае остальные 4 пальца направлены на силовые линии, в данном примере — на искомое направление нормали n к рамке. Силовые линии всегда замкнуты.
Определение
Вектор магнитного момента рамки с током — это вектор, направление которого совпадает с нормалью к плоскости рамки, а его величина равна произведению силы тока, проходящего через рамку, на ее площадь (p_m=IS).
Единица измерения магнитного момента — Ампер ⋅ м2.
Изменения характеристик рамки, вызванные магнитным полем, отражает вектор магнитной индукции В.
Величина данного вектора равна максимальному вращающему механическому моменту сил М, взаимодействующему с рамкой. Механический момент ≈ магнитный момент рамки ⋅ sin угла поворота рамки.
Вектор магнитной индукции является главной силовой характеристикой магнитного поля и определяет силу действия поля на заряд. По направлению он совпадает с положительной нормалью n к рамке с током и перпендикулярен элементарному току и направлению силы магнитного поля.
Принцип суперпозиции вектора индукции магнитного поля
Результирующая индукция магнитного поля, возникающая благодаря наличию в пространстве нескольких проводников с током, равна векторной сумме полей, возникающих от каждого тока в отдельности.
Данное правило справедливо как для магнитного, так и для электрического поля.
Закон Био-Савара-Лапласа (БСЛ)
Магнитное поле любого тока может быть вычислено как векторная сумма полей, создаваемых отдельными элементарными участками тока.
Обозначение закона в векторной форме:
<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>d</mi><mover><mi>B</mi><mo>⇀</mo></mover><mo>=</mo><mfrac><msub><mi>μ</mi><mn>0</mn></msub><mrow><mn>4</mn><mi>π</mi></mrow></mfrac><mfrac><mrow><mi>I</mi><mfenced open="[" close="]"><mrow><mi>d</mi><mover><mi>l</mi><mo>⇀</mo></mover><mo>,</mo><mover><mi>r</mi><mo>⇀</mo></mover></mrow></mfenced></mrow><msup><mi>r</mi><mn>3</mn></msup></mfrac></math>
В скалярной форме:
\(d\overset\rightharpoonup B=\frac{\mu_0}{4\pi}\frac{Id\mathcal l\sin\alpha}{r^2}\)
Модификации закона Био-Савара-Лапласа:
Магнитное поле прямого тока: \(\mathrm B=\frac{{\mathrm{μμ}}_02\mathrm I}{4\mathrm{πR}}\)
Магнитное поле кругового тока: \(\mathrm B=\frac{{\mathrm{μμ}}_0\mathrm I}{4\mathrm{πR}}\)
Обозначения:
\(\mu_0\) — магнитная постоянная;
\(\mu\) — относительная магнитная проницаемость среды;
\(dB\) — магнитная индукция;
I — сила тока;
R — расстояние от провода до точки определения магнитной индукции;
α — угол между вектором dl и r.
Если же взять за точку отсчета точку, в которой нужно найти вектор магнитной индукции, то формула немного упрощается:
\(d\overset\rightharpoonup B=\frac{\mu_0}{4\pi}\frac{I\left[\overset\rightharpoonup r\times d\overset\rightharpoonup r\right]}{r^3}=\frac I{10^7}\frac{\left[\overset\rightharpoonup r\times d\overset\rightharpoonup r\right]}{r^3},\)
где r — вектор, описывающий кривую проводника с током I, dr — элемент проводника.
Теорема о циркуляции вектора магнитной индукции
Данная теорема является следствием принципа суперпозиции и закона Био-Савара-Лапласа.
Циркуляция вектора магнитной индукции по произвольному замкнутому контуру равна алгебраической сумме токов, пересекающих поверхность, ограниченную этим контуром, умноженной на магнитную постоянную.
\(\oint_L(\overset\rightharpoonup Bd\overset\rightharpoonup{\mathcal l)}=\mu_0{\textstyle\sum_{}}I_i\)
Формула для расчета вектора магнитной индукции прямолинейного тока, исходя из теоремы:
\(\oint_S\;B_{\mathcal l}d\mathcal l=\;B\oint_Sd\mathcal l=B2\pi R=\mu_0I, откуда В=\frac{\mu\cdot l}{2\mathrm{πR}}\)
Магнитный поток
Магнитный поток пропорционален числу силовых линий вектора магнитной индукции, пронизывающих определенную площадь. Выражается в веберах (Вб).
\(x = {-b \pm \sqrt{b^2-4ac} \over 2a}Ф=BS\cos\alpha,\)
где Ф — магнитный поток, В — модуль вектора магнитной индукции, S — площадь, ограниченная контуром, а alpha — угол между векторами магнитной индукции и нормали к поверхности.
Обозначение через циркуляцию векторного потенциала А: \(Ф\;=\oint_L\;А\cdot dl.\)
В данной статье были рассмотрены основные формулы и понятия, связанные с вектором магнитной индукции.
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так