Какие углы называются вертикальными: определение и свойства
Вертикальные углы — что это такое в геометрии, определение
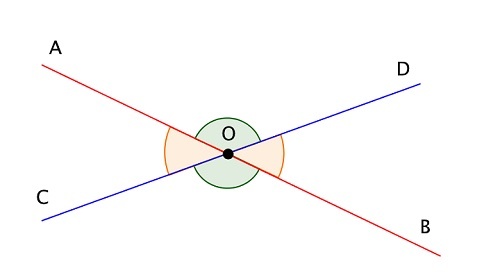
Вертикальные углы – пара углов с общей вершиной, которые образованы при пересечении двух прямых таким образом, что стороны одного из них являются продолжением сторон другого. Иными словами – они противоположны.
Свойства вертикальных углов
- Когда две прямые пересекаются, то образуется две пары вертикальных углов.
- Синусы, косинусы и тангенсы их равны.
- В сумме два вертикальных угла создают полный угол. Его градус равняется 360^\circ.
Равны или нет, доказательство теоремы
Особенность вертикальных углов в том, что они абсолютно идентичны.
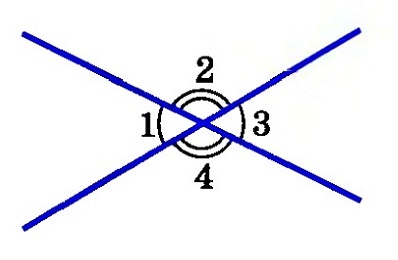
Убедимся в справедливости этого свойства. Докажем его: на чертеже 1 и 2, 2 и 3, 3 и 4, 4 и 1 являются смежными, 1 и 3, 2 и 4 – вертикальные.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
По свойству смежных углов, в сумме они дают \(180^\circ\). Используем этот признак и получаем:
\(\angle1+\angle2=180^\circ и \angle2+\angle3=180^\circ\)
Отсюда выведем, что:
\(\angle1=180^\circ-\angle2, \angle3=180^\circ-\angle2\)
Уравнение доказало равенство углов 1 и 3.
Примеры решения задач
Задача 1
Дано
\(\angle1=45^\circ\)
Найти: значения \(\angle2, \angle3, \angle4\)
Решение
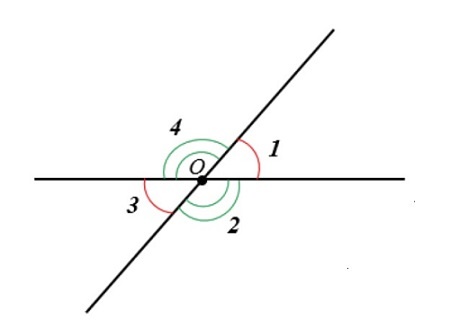
\(\angle1\) и \(\angle3\) вертикальные. Значит \(\angle1=\angle3=45^\circ.\)
\(\angle1\) и \(\angle4\) смежные. По правилу о смежных углах:
\(\angle1+\angle4=180^\circ\)
\(\angle4=180^\circ-\angle1=180^\circ-45^\circ=135^\circ\)
Так как \(\angle4\) и \(\angle2\) вертикальные, то \(\angle4=\angle2=135^\circ.\)
Ответ: величина \(\angle3=45^\circ,\) величина \(\angle2\) и \(\angle4=135^\circ.\)
Задача 2
Дано
Две прямые пересеклись и сформировали четыре угла. Сумма двух из них составляет \(140^\circ.\)
Найти: значения всех углов, образовавшихся при пересечении прямых.
Решение
Поскольку по условию пара углов образует \(140^\circ\), это дает право сделать вывод – они вертикальные, так как смежные в сумме должны достигать \(180^\circ\).
Так как вертикальные углы равны, то значение каждого из них соответствует:
\(140/2=70=70^\circ\)
Оставшиеся углы – смежные к вертикальным и вертикальные по отношению друг к другу. Для того, чтобы их вычислить, выполним следующее действие:
\(180-70=110=110^\circ\)
Ответ: \(70^\circ\), \(110^\circ\), \(70^\circ\), \(110^\circ\).
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так