Внешний угол треугольника
Как выглядит внешний угол треугольника
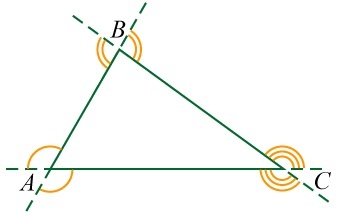
Внешний угол треугольника — это часть плоскости, ограниченной двумя лучами, исходящими из одной точки, которая равна разности между 180° и внутренним углом. Ее диапазон значений — от 0° до 180°.
Среди свойств ВУТ выделяют:
- сумма ВУ треугольника, взятых по одному при каждой точке соединения сторон, равняется 360°;
- ВУТ приравнивается к сумме двух углов треугольника, не смежных с ним: \angle1=\angle B+\angle C;
- при одной точке соединения сторон сумма внешнего и внутреннего углов составляет 180°.
Следует отметить, что у каждого треугольника есть два угла, которые являются смежными с ним. Получается, что у данной геометрической фигуры шесть внешних углов.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Чему равен, как найти при вершине
Для того, чтобы найти ВУТ при вершине, необходимо сложить значения не соседних с ним частей плоскости, которые ограничены двумя лучами, рассматриваемой геометрической фигуры.
Продемонстрируем это положение на примерах.
Задача №1
В треугольнике DEF угол D = 50°, а F = 45°. Найти: ВУ при каждой вершине фигуры.
Решение
Сумма углов треугольника всегда равна 180°. Из этого следует, что \angle E=180˚-\angle D-\angle F=85^\circ. ВУ при точке соединения сторон DE и DF будет равняться сложенным внутренним углам при вершинах E и F, а это 130°. Соответственно, ВУ при E составляет 95°, а при F — 135°.
Ответ: ∠ D = 130°, ∠ E = 95°, ∠ F = 135°.
Задача №2
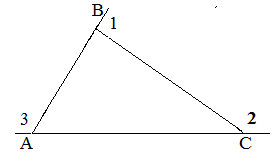
В треугольнике ABC ВУ при вершине A = 68°, а при вершине C = 55°. Найти: Внутренний угол при B. На иллюстрации отображены пронумерованные названия углов.
Решение
Если сложить смежные углы, то в любом случае получится 180°. Из этого составляем равенства: ∠ A = 180° – ∠ 3 = ∠ 180° – 112° = 68°; ∠ С = 180° – ∠ 2 = ∠ 180° – 125° = 55°. Далее из сложенного вычитаем уже известное: ∠ A = 180° – ∠ A – ∠ C = ∠ 180° – 68° – 55° = 57°.
Ответ: ∠ B = 57°.
Теорема о внешнем угле треугольника, доказательство
Теорема о ВУТ звучит следующим образом: внешний угол треугольника равняется сумме двух других, не смежных с ним.
Доказательство
Предположим, что MNP — треугольник с внешним углом q. Углы n и q являются соседними, поэтому их сумма составляет 180°. Из этого следует, что q = 180° – n. Согласно теореме о сумме углов треугольника n = 180° – (m + p). Поэтому m + p = 180° – n. Вследствие того, что q = 180° – n, то q = m + p. Теорема доказана.
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так