Правила возведения в степень комплексного числа
Возведение комплексного числа в степень
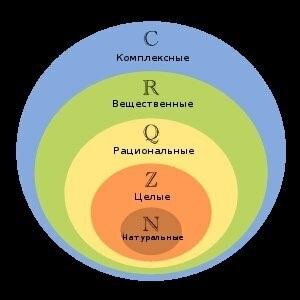
С началом учебы школьникам предстоит, помимо других предметов, осваивать принципы, закономерности, положения и теории математики. Как правило, новую тему начинают с повторения изученного материала, а именно, рассуждают о числах. В начальных классах учащимся передавали знания о натуральных числах. Затем предмет усложнялся, а школьники узнавали о других числовых множествах. Представим их на общей схеме:
Источник: dzen.ru
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Рассмотрим участок, закрашенный синим цветом. Здесь расположены комплексные числа. Разобраться в этом понятии можно путем решения простого уравнения:
\(х^{2} + 1 = 0\)
Попробуем определить, чему равны корни записанного выражения. В результате получим следующее равенство:
\(х^{2} = -1\)
Заметим, что при выполнении данного равенства неизвестное нужно возвести во вторую степень и получить при этом отрицательное число. По причине наличия подобных уравнений и необходимости в их решении были введены комплексные числа.
На уроках алгебры ученикам приходится решать множество заданий на разные операции с числами. В большинстве задач и тестов их требуется умножить, поделить или представить в виде какой-либо степени. Реализовывать подобные операции допустимо без учета формата рассматриваемых чисел. В том случае, когда определенное число записано как алгебраическое, то представить его в некой степени, равной n, удобно путем вычисления произведения n идентичных множителей.
Если имеется пара комплексных чисел, к примеру, \(z_{1} =a_{1} +b_{1} i и z_{2} =a_{2} +b_{2} i\), то для получения в итоге их произведения аналогично комплексного числа нужно учитывать алгебраические законы и условие, что \(i^{2} =-1\).
Итог умножения пары чисел, являющихся комплексными, например, \(z_{1} =r_{1} \cdot (\cos \varphi _{1} +i\sin \varphi _{1} )\) и \(z_{2} =r_{2} \cdot (\cos \varphi _{2} +i\sin \varphi _{2} )\), представляет собой комплексное число, полученное по итогам следующих вычислений: \(z_{1} \cdot z_{2} =r_{1} \cdot r_{2} \cdot \cos (\varphi _{1} +\varphi _{2} )+i\sin (\varphi _{1} +\varphi _{2} )\)
Интерес представляет история введения в обиход комплексного числа. Изначально мысль о том, что требуется использовать такие числа, зародилась в процессе формализованного поиска ответов на уравнения с неизвестными в третьей степени. При этом в выражении Кардано образовывалось число со знаком минуса, заключенное под знак квадратного корня. Огромное значение для изучения комплексных чисел имеют труды Эйлера, Декарта и Гаусса. К примеру, известный научный деятель в области математики, Эйлер обозначил мнимую единицу за i. Непосредственно понятие комплексного числа было зафиксировано в 1831 году. Автором научного термина является Гаусс.
Возведение в степень в показательной и тригонометрической форме, формула Муавра
В процессе работы с комплексными числами, а именно, их умножении, можно упростить себе задачу, если трансформировать множители в показательную или тригонометрическую форму. В том случае, когда комплексное число имеет вид алгебраического, целесообразно переписать его по-другому, например, выбрать для записи любой из вышеуказанных форматов.
Возвести комплексное число, записанное в показательном виде, в какую-нибудь степень можно с помощью данного соотношения:
\(z^k = (re^{i\varphi})^k = r^k e^{ik\varphi}, k \in Z\)
Если число, являясь комплексным, представлено в тригонометрической форме, то его возводят в степень с помощью следующего выражения:
\(z^k = r^k (\cos k\varphi + i\sin k\varphi), k \in N\)
Формула Муавра гласит, что степень с порядком \(n (n\in Z_{+})\) для некого комплексного числа \(z=r\cdot (\cos \varphi +i\sin \varphi )\), определяется как комплексное число, равное: \(z^{n} =r^{n} \cdot (\cos n\varphi +i\sin n\varphi ).\)
В действительности формулу Муавра несложно получить путем последовательных преобразований. К примеру, можно самостоятельно умножить рассматриваемое комплексное число \(z=r\cdot (\cos \varphi +i\sin \varphi )\) на идентичное комплексное число в течение такого количества раз, которое равно n.
Исходя из закономерности Муавра, допустимо сделать вывод о том, что при возведении какого-то комплексного числа в целую степень со знаком плюс, требуется модуль этого числа возвести в заданную степень, а аргумент, принадлежащий рассматриваемому комплексному числу, умножить на степенной показатель.
Не все задания можно решить одним простым действием. Встречаются задачи, где показателем степени, в которую возводят комплексное число, является большим числом. Тогда не нужно тратить время и силы на бесконечные операции умножения этого числа на само себя. Целесообразно упростить решение путем поэтапного выполнения следующего алгоритма:
- записать алгебраическое комплексное число в тригонометрическом формате;
- выполнить возведение в степень полученного числа, руководствуясь соотношением Муавра;
- если это потребуется, выполнить обратное действие и записать полученный результат в алгебраической форме.
Комплексные числа, а также функции с ними, характеризуются особыми возможностями. С помощью специальных свойств таких чисел можно значительно упростить и повысить качество решений математических, физических и технических задач. К примеру, таким способом обрабатывают сигналы, находят ответы к задачам по теории управления, колебательных движений, электрическом магнетизме. При составлении карт и в гидродинамической предметной области активно применяют трансформации комплексной плоскости. Система, состоящая из комплексных чисел, лежит в основе квантовой механики. Эти знания позволяют сформировать понимание современного физического мира.
Исходя из полученной информации, можно с легкостью решать примеры на представлении комплексных чисел в той или иной степени. При этом не нужно множество раз умножать такое число само на себя. Достаточно внимательно изучить предложенное выражение и применить полученные знания на практике. С другой стороны, имеется несколько способов возведения в степень разных чисел. В качестве примера можно привести бинарное возведение в степень. В таком случае в процессе вычислений используют специальную формулу, сокращающую количество раз, в течение которых требуется выполнить умножение числа само на себя.
Примеры решения задач
В процессе решения примеров с комплексными числами, которые требуется представить в виде той или иной степени, необходимо руководствоваться стандартным алгоритмом действий. Начинать расчеты следует с определения вида уравнения. Поняв, какие действия нужно выполнить, можно вспомнить полезную формулу. Далее остается лишь применить закономерность, либо преобразовать выражение в подходящий формат. Не следует забывать о таком важном условии, как область допустимых значений. Подобная проверка позволит исключить посторонние корни.
Дано комплексное число, которое требуется возвести во вторую степень: \(z = \sqrt{2}e^{\frac{\pi}{2}i}\)
Решение
Воспользуемся уже известной формулой, чтобы представить во второй степени модуль и экспоненту. Запишем поэтапные вычисления согласно стандартному алгоритму и получим искомое значение:
\(z^2 = (\sqrt{2}e^{\frac{\pi}{2}i})^2 = 2e^{\pi i}\)
Ответ: \(z^2 = 2e^{\pi i}\)
Требуется выполнить возведение комплексного числа z в степень, равную трем, при условии, что комплексное число записано в таком виде: \(z = 1+\sqrt{3}i\)
Решение
Заметим, что формат записи данного числа алгебраический. Исходя из полученных знаний, стоит сначала перевести z в тригонометрическую форму. Таким образом, вычисления получится значительно упростить. Определим, чему равен модуль заданного числа:
\(|z| = \sqrt{a^2+b^2} = \sqrt{1^2 + (\sqrt{3})^2} =\sqrt{4}=2\)
Далее можно приступить к поиску аргумента:
\(\varphi = \frac{b}{a} = arctg \frac{\sqrt{3}}{1} = \frac{\pi}{3} \)
В итоге получается следующая тригонометрическая запись рассматриваемого комплексного числа:
\(z = 2(\cos \frac{\pi}{3} + i\sin \frac{\pi}{3})\)
Если действовать согласно стандартному алгоритму, то на втором этапе нужно вычислить представленное комплексное число в третьей степени:
\(z^3 = 2^3(\cos (3 \cdot \frac{\pi}{3})+i\sin (3 \cdot \frac{\pi}{3})) = 8 (\cos \pi + i\sin \pi)\)
В конце расчетов стоит выполнить обратный перевод числа в алгебраический формат. В результате получим:
\(z^3 = 8 (-1 + i \cdot 0) = -8\)
Ответ: \(z^3 = -8\)
Нужно применить полученные из курса теории знания и возвести комплексное число z в степень n с учетом следующих условий: \(z=1+2\cdot i n=2..4\)
Решение
Вспомним, как умножают комплексные числа, если они записаны в алгебраическом формате. Руководствуясь основным определением, стандартной формулой и подставив исходные данные, получим следующие результаты вычислений:
\(z^{2} =(1+2\cdot i)\cdot (1+2\cdot i)=-3+4i\)
\(z^{3} =z^{2} \cdot (1+2\cdot i)=-3+4i-6i-8=-11-2i\)
\(z^{4} =z^{3} \cdot (1+2\cdot i)=-11-2i-22i+4=-7-24i\)
Ответ: \(-3+4i , -11-2i, -7-24i.\)
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так