Вокруг какого параллелограмма можно описать окружность
Окружность, описанная вокруг параллелограмма
Окружность описана вокруг параллелограмма, если все его вершины лежат на этой окружности. Параллелограмм, около которого описана окружность, называется вписанным в окружность.
Вокруг какого параллелограмма можно описать окружность: необходимые условия
Чтобы описать вокруг параллелограмма окружность, он должен соответствовать определенным условиям.
В любом вписанном в окружность четырехугольнике сумма противоположных углов равна 180°.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Параллелограмм — частный случай четырехугольника. В соответствии с теоремой, чтобы описать окружность около параллелограмма или, другими словами, вписать параллелограмм в окружность, нужно чтобы сумма его противолежащих углов была равна 180°.
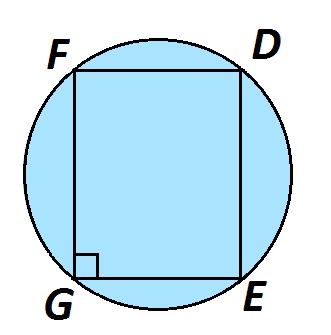
Так как у параллелограмма противоположные углы равны, каждый из этих двух углов будет равен 90°. То же самое можно сказать и о второй паре противолежащих углов. Все углы вписанного в окружность параллелограмма будут прямые, а параллелограмм с четырьмя прямыми углами — это прямоугольник. Следовательно, описать окружность можно только около прямоугольника (в том числе квадрата).
Где будет центр такой окружности
Центр окружности, описанной около параллелограмма (прямоугольника), совпадает с точкой пересечения диагоналей параллелограмма.
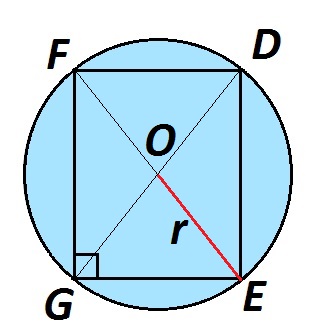
На изображении ниже EGFD — прямоугольник. Его диагонали EF и GD равны между собой, пересекаются в точке О и делятся точкой пересечения пополам.
Точка О равноудалена от четырех вершин прямоугольника EGFD и является центром описанной окружности. Отрезки ОЕ, ОG, ОF, ОD — радиусы описанной окружности.
Формула расчета радиуса окружности, описанной около параллелограмма
Диагональ параллелограмма равна диаметру описанной около него окружности, соответственно радиус описанной окружности равен половине диагонали. При этом нужно помнить, что параллелограмм, вокруг которого можно описать окружность, является прямоугольником и обе его диагонали равны.
\(R=\frac12d,\)
где R — радиус описанной окружности,
d — диагональ параллелограмма.
Если известны стороны прямоугольника, то в соответствии с теоремой Пифагора формула будет иметь следующий вид:
\(R=\frac{\sqrt{a^2+b^2}}2,\)
где R — радиус описанной окружности,
a и b — стороны параллелограмма.
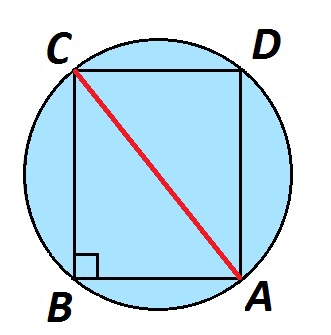
Дано: прямоугольник АВСD со сторонами 6 см и 8 см. Около АВСD описана окружность.
Найти: радиус описанной окружности.
Решение:
Рассмотрим прямоугольный треугольник АВС. Его гипотенуза АС равна диаметру окружности, описанной около прямоугольника АВСD.
\(АС=\sqrt{АВ^2+ВС^2}=\sqrt{6^2+8^2}=\sqrt{36+64}=\sqrt{100}=10 (см).\)
\(R=\frac{АС}2=\frac{10}2=5 (см).\)
Ответ: радиус описанной окружности равен 5 см.
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так