Окружность, вписанная в трапецию
Что такое окружность, вписанная в трапецию
Окружность можно вписать в любой треугольник. Однако это утверждение нельзя применить к любому из четырехугольников.
Прежде чем приступить к рассмотрению темы о вписанной в трапецию окружности, дадим определение вписанной окружности.
Вписанной в многоугольник окружностью называют окружность, которая касается каждой из сторон многоугольника в одной точке. Многоугольник в этом случае называют описанным около окружности.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Теорема о вписанной окружности: в произвольный выпуклый четырехугольник можно вписать окружность тогда и только тогда, когда суммы его противоположных сторон равны.
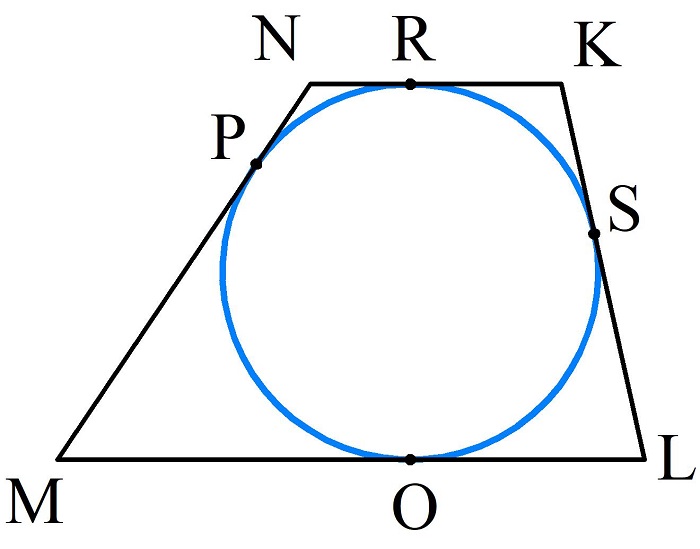
Доказательство: пусть имеется произвольный четырехугольник MNKL и вписанная в него окружность. Обозначим точки касания окружности со сторонами четырехугольника как O, P, R, S.
Если касательные проведены из одной точки, то отрезки, построенные от этой точки до точки касания с окружностью, равны. Тогда KS=KR, LS=LO, MO=MP, NR=NP. Вычислим суммы противоположных сторон: MN+KL=(MP+NP)+(KS+LS) и NK+ML=(NR+KR)+(MO+LO).
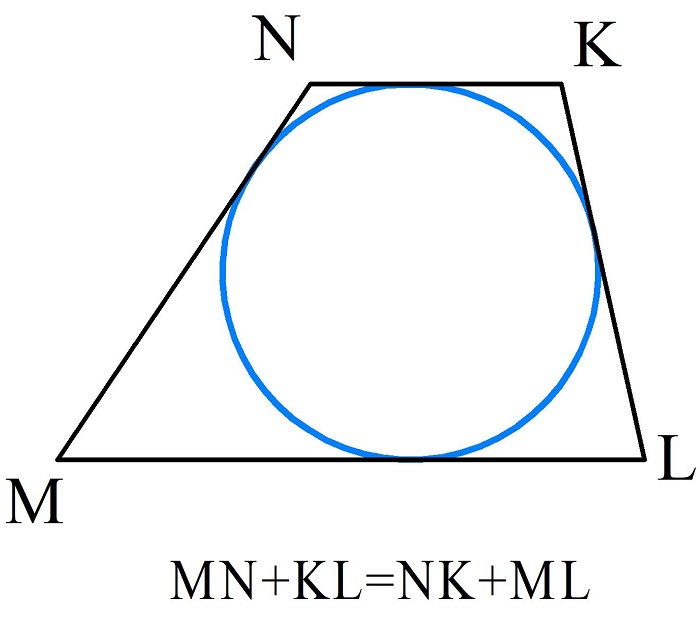
Из равенства отрезков получим, что MN+KL= NK+ML.
Четырехугольник считают выпуклым, если он расположен в одной полуплоскости относительно линии, проходящей через любую из его сторон.
Трапеция является выпуклым четырехугольником. При этом две параллельные стороны трапеции называют основаниями, а две остальные — боковыми сторонами.
Тогда необходимым условием наличия вписанной окружности в трапецию будет равенство суммы ее оснований и боковых сторон.
Для обратного случая — окружность описана вокруг трапеции, трапеция должна быть равнобедренной, то есть ее боковые стороны должны быть равными.
Рассмотрим свойства вписанной в трапецию окружности.
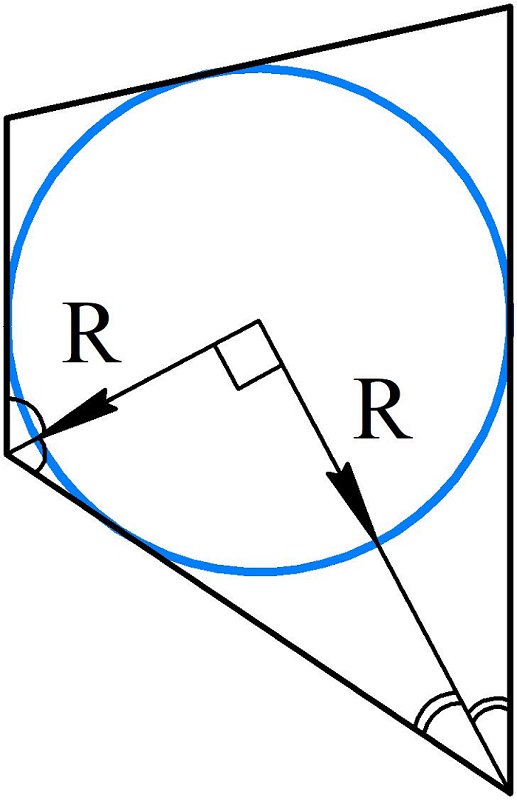
Из свойства биссектрис при боковых сторонах трапеции следует, что радиусы вписанной окружности, проведенные к вершинам боковой стороны и лежащие на биссектрисах, образуют прямой угол.
Биссектрисы трапеции пересекаются под углом 90°.
Радиус вписанной окружности, проведенный к точкам касания, перпендикулярен сторонам трапеции (по свойству перпендикулярности радиуса и касательной).
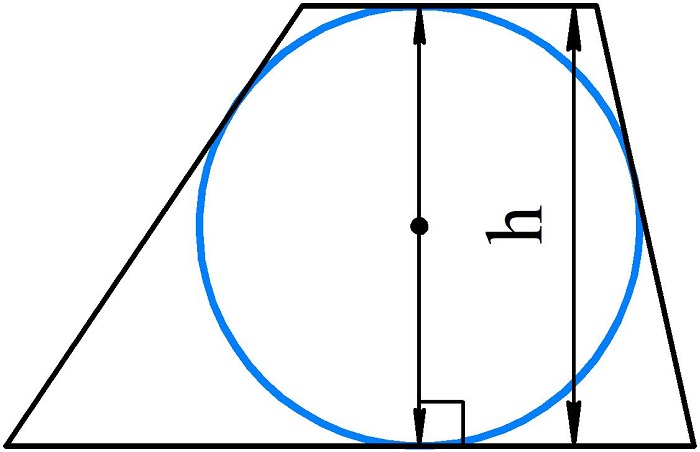
Из предыдущего свойства вытекает следующее: радиус вписанной окружности равен половине высоты трапеции, а диаметр — полной длине высоты.
Высота трапеции — прямая, опущенная от одного основания к другому под прямым углом.
Где находится центр такой окружности
Для построения и решения задача необходимо определить, где расположен центр вписанной окружности.
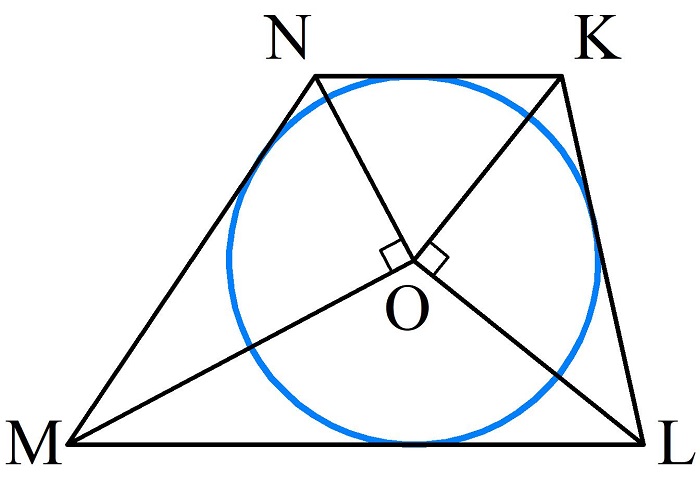
Центр окружности, вписанной в трапецию, лежит в точке пересечения биссектрис.
Биссектрисы трапеции пересекаются под прямым углом, отсюда можно сделать следующий вывод: треугольники MON и KOL — прямоугольные.
Формулы для расчета
Основными характеристиками любой окружности являются радиус и диаметр.
Точка касания окружности радиусом R и боковой стороны делит последнюю на два отрезка v и q. Тогда формула для вычисления радиуса будет иметь вид:
\(R=\sqrt{v\cdot q}\)
Если трапеция равнобедренная и сумма длин оснований равна двум длинам боковой стороны, радиус вписанной окружности:
\(R=\frac{\sqrt{v\cdot q}}2\)
Диаметр равен длине двух радиусов, значит:
\(D=2\sqrt{v\cdot q}\)
Формула радиуса через высоту трапеции:
\(R=\frac h2\)
Диаметр через высоту:
D=h
Если значение высоты неизвестно, ее можно найти через длины диагоналей \(d_1\) и \(d_2\) и оснований a и b трапеции:
\(h=\frac{d_1\cdot d_2}{a+b}\sin\gamma\)
где γ — угол между диагоналями трапеции.
Площадь вписанной окружности через параметры трапеции (высоту, отрезки боковой стороны):
\(S=\pi R^2=\frac14\pi h^2\)
или
\(S=\pi R^2=\pi\cdot v\cdot q\)
В случае равнобедренной трапеции:
\(S=\pi R^2=\frac{\pi\cdot v\cdot q}4\)
Периметр вписанной окружности через параметры трапеции:
\(P=2\mathrm{πR}=\mathrm{πh}\)
или
Если трапеция равнобедренная:
\(P=2\mathrm{πR}=\mathrm\pi\sqrt{\mathrm{vq}}\)
Приведем формулы для вычисления произвольной и равнобедренной трапеции через радиус вписанной окружности R.
Площадь трапеции:
\(S=\frac{a+b}2h=(a+b)R\)
Полусумма оснований a и b равна средней линии l, тогда:
\(S=2\cdot l\cdot R\)
Площадь равнобедренной трапеции:
\( S=\frac{4R^2}{\sin\alpha}\)
где α — угол между основанием и боковой стороной.
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так