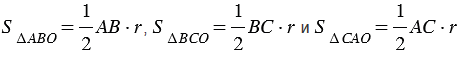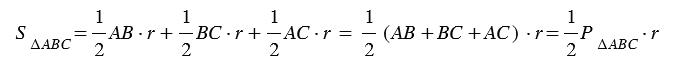Все про вписанные и описанные окружности
Вписанные и описанные окружности
Окружность, описанная около выпуклого многоугольника, представляет собой такую окружность, которая касается каждой из вершин этого многоугольника.
Вписанным называют многоугольник, около которого описана окружность.
Рассмотрим наглядный пример:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
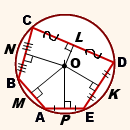
На рисунке изображена окружность с центром, обозначенным как О. Радиус этой окружности равен R. Она описана около многоугольника с пятью углами ABCDE, который по определению является вписанным. Заметим, что в точке О пересекаются серединные перпендикуляры к граням ABCD, то есть:
\(AP = PE,OP \bot AE\),
\(AM = MB,OM \bot AB\),
\(BN = NC,ON \bot BC\),
\(CL = LD,OL \bot CD\),
\(DK = KE,OK \bot DE\).
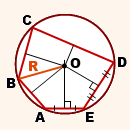
Здесь точка О расположена на одинаковом расстоянии от вершин пятиугольника. Рассмотреть это можно на рисунке:
Точка О удалена от каждой из вершин пятиугольника на расстояние, которое равно радиусу описанной окружности:
OA=OB=OC=OD=OE=R.
Заметим, что около любого треугольника, допустимо описать окружность.
Окружность, вписанная в выпуклый многоугольник, представляет собой такую окружность, которая проходит через все стороны рассматриваемого многоугольника, а каждая из его сторон является касательной к вписанной окружности.
Описанным многоугольником называют такой многоугольник, в который вписана окружность.
Рассмотрим пример вписанной в многоугольник окружности:
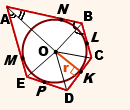
Центр окружности обозначен точкой О, а радиус равен r. Данная окружность вписана в многоугольник с пятью углами ABCDE, который по определению является описанным. В точке О пересекаются биссектрисы геометрической фигуры ABCD, то есть:
\(\angle EAO = \angle BAO\),
\(\angle ABO = \angle CBO\),
\(\angle BCO = \angle DCO\),
\(\angle CDO = \angle EDO\),
\(\angle AEO = \angle DEO\).
Точка О находится на одинаковом расстоянии от каждой из точек касания. Точка О удалена от каждой стороны на величину радиуса:
OK=OL=ON=OM=OP=r.
Вершины многоугольника ABCDE расположены на одинаковом расстоянии от точек касания, которые им соответствуют:
AM=AN,
BN=BL,
CL=CK,
DK=DP,
EP=EM.
Вписанная в какой-то описанный многоугольник окружность имеет радиус, равный:
\(r = \frac{S}{p}\)
Здесь S обозначает величину площади, которой характеризуется многоугольник, p является полупериметром этого многоугольника.
Соотношения радиусов вписанной и описанной окружности можно выразить с помощью формулы Эйлера. Таким образом, при d, равном расстоянию между центральными точками вписанной и описанной окружностей, имеющими радиусы r и R соответственно, справедливо следующее соотношение:
\(d^{2}=R^{2}-2Rr.\)
Существует несколько формул, согласно которым можно сформулировать отношения и произведения радиусов рассматриваемых окружностей:
\({\frac {r}{R}}={\frac {4S^{2}}{pabc}}=\cos \alpha +\cos \beta +\cos \gamma -1,\)
\(2Rr={\frac {abc}{a+b+c}},\)
\({\frac {r}{R}}=4\sin {\frac {\alpha }{2}}\sin {\frac {\beta }{2}}\sin {\frac {\gamma }{2}}=\cos \alpha +\cos \beta +\cos \gamma -1.\)
Здесь p обозначает полупериметр треугольника, а S является его площадью.
Заметим, что если опустить перпендикуляры к сторонам треугольника в точки касания вписанных окружностей, то эти прямые будут обладать единственной точкой пересечения. Данная точка симметрична центру вписанной окружности по отношению к центральной точке описанной окружности.
Теоремы вписанной и описанной окружности, свойства
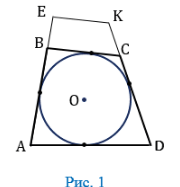
Вписанная в многоугольник окружность касается каждой из его сторон. Ее центральная точка находится во внутренней области многоугольника. В качестве примера приведем окружность и два многоугольника:
Здесь четырехугольник АВСD является описанным около окружности, центр которой обозначен точкой О. Четырехугольник АЕКD нельзя назвать описанным, так как одна из его сторон ЕК не является касательной к окружности.
В какой-либо треугольник допустимо вписать окружность.
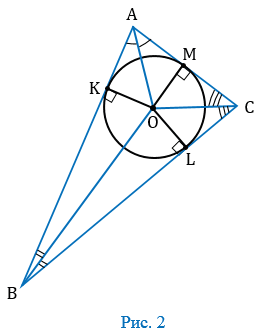
Докажем данную теорему на примере некого треугольника АВС. Для этого построим биссектрисы углов А, В и С, пересекающиеся в точке О, что является следствием свойства биссектрис. Опустим из центра О перпендикуляры к сторонам АВ, ВС и СА и обозначим их ОК, ОL и ОМ.
Заметим, что центр О находится на одинаковом расстоянии от сторон треугольника АВС по свойству биссектрис. Таким образом:
ОК = ОL = ОМ
В результате, окружность с центральной точкой О и радиусом, равным ОК, обладает точками К, L и М. Стороны треугольника АВС являются касательными к данной окружности, а точки касания соответствуют К, L, М, исходя из их перпендикулярности радиусам ОК, ОL и ОМ.
Следовательно, окружность с центром О и радиусом, равным ОК, вписана в треугольник АВС. В итоге теорема доказана.
Из рассматриваемой теоремы о вписанной окружности вытекает несколько следствий. Рассмотрим их детально.
В какой-либо треугольник можно вписать лишь одну окружность.
В качестве доказательства этого утверждения, предположим, что в какой-то треугольник допустимо вписать две окружности. В таком случае их центральные точки расположены на одинаковом расстоянии от граней треугольника и в результате совпадают с центральной точкой О, в которой пересекаются биссектрисы углов треугольника.
Радиус окружностей можно вычислить, как расстояние от точки О до сторон треугольника. Можно сделать вывод о том, что рассматриваемые окружности совпадают, и в треугольник допустимо вписать единственную окружность.
Площадь треугольника определяется, как его полупериметр, умноженный на радиус окружности, которая вписана в искомый треугольник.
Вернемся к последнему рисунку. Треугольник АВС можно условно поделить на три треугольника:
АВО;
ВСО;
САО.
Предположим, что АВ, ВС и АС являются основаниями перечисленных треугольников. В таком случае:
ОК = ОL = ОМ = r
Здесь r обозначает радиус окружности с центральной точкой О. Тогда:
Исходя из свойства площадей:
Тогда АВ + ВС + АС = Р, то есть периметру треугольника. Следствие доказано.
Какую-либо окружность можно вписать не в каждый четырехугольник.
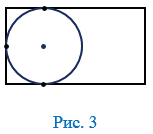
В качестве примера рассмотрим четырехугольник, являющийся прямоугольником:
В какой-либо четырехугольник можно вписать окружность при условии, что суммы его противоположных граней равны.
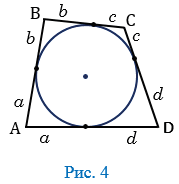
Рассмотрим следующий четырехугольник и вписанную в него окружность:
Отрезки касательных к окружности, которые проведены из одной точки, являются равными друг другу. В таком случае:
АВ + CD = a + b + c + d
ВС + АD = a + b + c + d
Тогда:
АВ + CD = ВС + АD
В том случае, когда выпуклый четырехугольник обладает противоположными сторонами, суммы которых попарно равны, в данный четырехугольник можно вписать окружность.
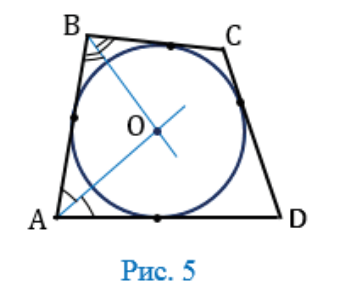
Предположим, что в некотором четырехугольнике АВСD:
АВ + СD = ВС + АD
Построим окружность:
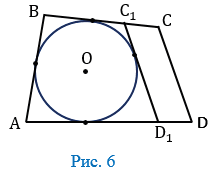
Когда окружность касается также стороны CD, она будет вписана в четырехугольник. В противном случае CD является секущей, либо не обладает общими точками с окружностью. Построим параллельную ей прямую.
Заметим, что АВС1D1 является описанным четырехугольником, поэтому:
АВ + С1D1 = ВС1 + AD1
С другой стороны:
ВС1 = ВС - С1С
АD1 = АD - D1D
В результате:
С1D1 + С1С + D1D = ВС + АD – АВ
Выражение слева равно CD, таким образом:
С1D1 + С1С + D1D = СD
Получается, что какая-то сторона в четырехугольнике равна трем другим сторонам в сумме. Это противоречит свойству четырехугольника и является ошибочным утверждением. Аналогичным способом можно представить доказательства того, что CD не является секущей к окружности. Тогда рассматриваемая окружность касается стороны CD.
Вписанная окружность обладает следующими свойствами:
- Биссектрисы внутренних углов описанного многоугольника пересекаются в центре окружности, которая вписана в данный многоугольник.
- В какой-либо треугольник допустимо вписать не более одной окружности.
- Вписанная окружность имеет радиус, который вычисляется как отношение площади описанного треугольника к его полупериметру.
- Вписать окружность можно исключительно в выпуклый четырехугольник.
- Допустимо вписать окружность в выпуклый многоугольник с четырьмя углами при условии, что суммы его противоположных сторон одинаковы.
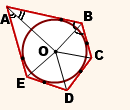
Вписанный в окружность многоугольник обладает вершинами, которые лежат на описанной около него окружности. В качестве примера рассмотрим рисунок:
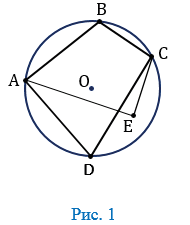
Заметим, что по определению четырехугольник АВСD является вписанным в окружность, центр которой находится в точке О. Четырехугольник АЕСD нельзя назвать вписанным, так как его вершина Е не расположена на окружности.
Около какого-либо треугольника допустимо описать окружность.
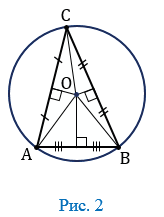
В качестве доказательства рассмотрим треугольник АВС. Построим серединные перпендикуляры к сторонам рассматриваемого треугольника. Эти прямые имеют точку пересечения, совпадающую с центром окружности О. Соединим ее с точками А, В, С.
Точка О расположена на одинаковом расстоянии от А, В и С:
ОА = ОВ = ОС
Тогда окружность с центром О пересекает каждую из вершин построенного треугольника. В результате эта окружность описана около треугольника АВС.
Около какого-либо треугольника можно описать не более одной окружности.
Если предположить обратное, то центры описанных окружностей будут находиться на одинаковом расстоянии от вершин вписанного треугольника. Радиус каждой из таких окружностей совпадет с расстоянием от точки О, в которой пересекаются серединные перпендикуляры к сторонам треугольника, до вершин. В результате рассматриваемые окружности совпадают.
Не в каждом случае около многоугольника с четырьмя углами можно описать окружность.
В качестве примера рассмотрим следующий рисунок:
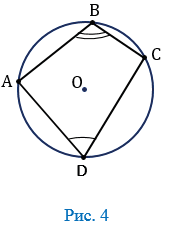
В каком-либо вписанном четырехугольнике противоположные углы в сумме составляют 180°.
Приведем пример вписанного четырехугольника ABCD:
В данном случае:
\(\angle В = ½ \smile АDС\)
\(\angle D = ½ \smile АВС\)
\(\angle В + \angle D = ½ \smile АDС + ½ \smile АВС = ½ ( \smile АDС + \smile АВС)\)
\(\smile АDС + \smile АВС = 360\circ\)
\(\angle В + \angle D = 1/2\times 360\circ = 180\circ\)
Обратное утверждение в математике звучит так: когда в четырехугольнике противоположные углы в сумме составляют 180°, около него можно описать окружность.
Окружность, которая описана около треугольника, обладает следующими свойствами:
- Вокруг какого-либо треугольника допустимо описать окружность, причем не более одной.
- Если около прямоугольного треугольника описана окружность, то ее центр расположен на середине гипотенузы.
- Радиус описанной около треугольника окружности определяется по формулам:
\(R=\frac{abc}{4S}\)
\(R=\frac{AB}{2\sin \angle C}=\frac{AC}{2\sin \angle B}=\frac{BC}{2\sin \angle A}\).
Окружность, которая описана около четырехугольника, обладает следующими свойствами:
- Вокруг какого-то четырехугольника допустимо описать окружность, когда его противоположные углы в сумме составляют 180°.
- Результат умножения диагоналей вписанного четырехугольника равен сумме произведений противоположных сторон.
- Правило Брахмагупты для расчета площади вписанного четырехугольника:
\(S=\sqrt{(p-a)(p-b)(p-c)(p-d)}\).
Свойства углов
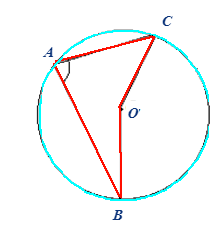
Вписанный угол в окружность является углом с вершиной, расположенной на этой окружности, и сторонами, пересекающими окружность.
Вписанные углы обладают следующими свойствами:
- Вписанный угол равен половине дуги, на которую он опирается.
- Вписанный угол равен половине центрального угла, опирающегося на аналогичную дугу: \(\angle BAC=\frac{1}{2}\angle BOC\)
- Если вписанные углы опираются на одинаковую дугу, то данные углы являются равными.
- Если вписанный угол опирается на диаметр окружности, то его градусная мера составляет 90°.
- Каждая из пар вписанных углов, опирающихся на одинаковую хорду и имеющих вершины, расположенные с разных сторон от хорды, в сумме дают 180°.
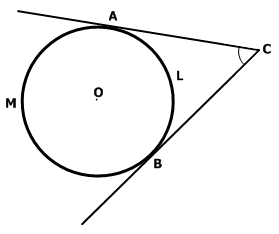
Описанным углом в геометрии называют такой угол, который образован с помощью пары касательных, выходящих из одной и той же точки.
Главное свойство (признак) заключается в том, что описанный угол равен половине разности дуг, которые заключены между сторонами этого треугольника:
\(\angle ACB = ½ (\smile АMB - \smile АLB)\)
Примеры задач на понятия вписанной и описанной окружности
Имеется некий равнобедренный (но не равносторонний) треугольник с гипотенузой А=6 см. В данный треугольник вписана окружность, радиус которой требуется вычислить с описанием решения.
Решение
Воспользуемся формулой:
\(r=\frac{S}{p}\)
Заметим, что стороны в равнобедренном треугольнике равны:
AB=BC
Введем переменную х для обозначения этих сторон. Применим теорему Пифагора, чтобы вычислить стороны:
\({{x}^{2}}+{{x}^{2}}=36\)
Тогда:
\(x=3\sqrt{2}\)
\(AB=BC=3\sqrt{2}\)
Вычислим площадь прямоугольного треугольника:
\(S=\frac{1}{2}AB\cdot BC=9 \ {{cm}^{2}}\)
Рассчитаем периметр:
\(p=\frac{AB+BC+AC}{2}=\frac{3\sqrt{2}+3\sqrt{2}+6}{2}=3\sqrt{2}+3=3(\sqrt{2}+1)\ cm\)
Далее вычислим радиус:
\(r=\frac{S}{p}=\frac{9}{3(\sqrt{2}+1)}=\frac{3}{\sqrt{2}+1}\ cm\)
Ответ: \(r=\frac{3}{\sqrt{2}+1} см\)
В многоугольник с четырьмя углами ABCD вписана окружность. Требуется вычислить стороны CD и AD, если CD больше по сравнению с AD в 3 раза, при этом AB=4 см, BC=10 см.
Решение
По определению описанного четырехугольника суммы его противоположных сторон равны:
AB+CD=BC+AD
Введем переменную х и обозначим с ее помощью AD. Тогда:
CD=3x
Таким образом:
4+3x=10+x
x=3
В результате:
\(AD=3\ cm, \quad CD=3\cdot 3=9\ cm\)
Ответ: AD=3 см, CD=9 см
Дан прямоугольный треугольник АВС с катетами: AB=3 см, AC=4 см.
Около данного треугольника описана окружность, радиус которой требуется определить.
Решение
Определим гипотенузу по теореме Пифагора и свойствам описанной окружности:
\(BC=\sqrt{A{{B}^{2}}+A{{C}^{2}}}=\sqrt{9+16}=5 \ cm\)
В результате:
\(R=\frac{1}{2}BC=2,5 см.\)
Ответ: R=2,5 см.
Дан четырехугольник ABCD, в котором угол А меньше по сравнению с углом В в 2 раза, угол С больше, чем угол D в 3 раза. Около данного четырехугольника описана окружность. Необходимо вычислить, чему равны углы этого четырехугольника.
Решение
Представим, что:
\(\angle A=x\)
В таком случае:
\(\angle B=2x\)
\(\angle D=y\)
Таким образом:
\(\angle C=3y\)
Сумма противоположных углов вписанного четырехугольника равна 180°:
\(\begin{cases} & x+3y=180, \\ & 2x+y=180. \\ \end{cases}\)
Решениями системы являются:
\(x=72, \quad y=36.\)
В результате:
\(\angle A={{72}^{\circ}},\ \angle B=2\cdot {{72}^{\circ}}={{144}^{\circ}},\ \angle D={{36}^{\circ}},\ \text{a}\ \angle C=3\cdot {{36}^{\circ}}={{108}^{\circ}}\)
Ответ: \(\angle A={{72}^{\circ}},\ \angle B={{144}^{\circ}}, \ \angle C={{108}^{\circ}}, \ \angle D={{36}^{\circ}}\)
Построена окружность, в которой проведена хорда АВ. С разных сторон от нее отметили точки C и D, соединенные с концами хорды. Образованный угол ACB больше по сравнению с углом ADB в 2 раза. Требуется вычислить, чему равны данные углы.
Решение
Введем обозначение угла:
\(\angle ADB=x\)
В таком случае:
\(\angle ACB=2x\)
Тогда:
\(x+2x=180\)
\(x=60\)
В результате:
\(\angle ADB={{60}^{\circ}},\ \text{a}\ \angle ACB={{120}^{\circ}}\)
Ответ: \(\angle ADB={{60}^{\circ}}, \ \angle ACB={{120}^{\circ}}\)
Имеется пара вписанных в окружность треугольников ABC и ABD. Угол D составляет 35°, а сторона BC пересекает центральную точку окружности. Нужно определить, чему равен угол АВС.
Решение
Выполним вычисления:
\(\angle C=\angle D={{35}^{\circ}}\)
\(\angle ABC={{180}^{\circ}}-\angle A-\angle C={{180}^{\circ}}-{{90}^{\circ}}-{{35}^{\circ}}={{55}^{\circ}}\)
Ответ: \(\angle ABC={{55}^{\circ}}\)
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так