Вписанный угол

Что такое вписанный угол

Вписанный угол опирается на дугу, образованную им на окружности, или опирается на хорду, которая соединяет концы этой дуги.

Свойства вписанного угла:

• любые вписанные углы, которые опираются на одну и ту же дугу, равны;
• любые вписанные углы, которые опираются на одну и ту же хорду, с вершинами, расположенными по одну сторону от этой хорды, равны;
• все вписанные углы, которые опираются на диаметр окружности, являются прямыми;
• каждая пара углов, которые опираются на одну и ту же хорду, с вершинами, расположенными по разные стороны хорды, составляют в сумме \(180^{0}.\)

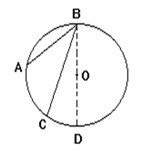
Согласно перечисленным правилам, можно значительно упростить измерение углов, вписанных в окружность. Например, пусть в окружность вписан четырехугольник ABCD с \(\angle A={{105}^{\circ}}\), \(\quad \angle B={{64}^{\circ}}\). Углы A и C опираются на одну хорду BD, но лежат по разные стороны от нее, и их сумма составляет \(180^{0}\). Таким образом:

\(\angle C={{180}^{\circ}}-\angle A={{180}^{\circ}}-{{105}^{\circ}}={{75}^{\circ}}\)

\(\angle D={{180}^{\circ}}-\angle B={{180}^{\circ}}-{{64}^{\circ}}={{116}^{\circ}}\)

Следовательно, \( \angle C={{75}^{\circ}}, \quad \angle D={{116}^{\circ}}\)

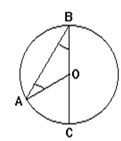
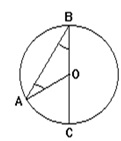
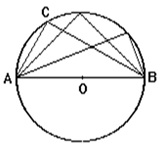
Можно рассмотреть пару треугольников ABC и ABD. Предположим, что Угол C равен \({{50}^{\circ}}\), сторона BD проходит через центр окружности. Также Треугольники ABC и ABD имеют общую сторону AB, на которую опираются углы C и D. Таким образом:

\(\angle C=\angle D={{50}^{\circ}}\)

Треугольник ABD обладает углом A, который является прямым. Это объясняется тем, что данный угол опирается на диаметр BD. Исходя из этого, можно найти угол В:

\(\angle B={{180}^{\circ}}-\angle A-\angle D={{180}^{\circ}}-{{90}^{\circ}}-{{50}^{\circ}}={{40}^{\circ}}\)

В результате \(\angle B={{40}^{\circ}}\)

Можно выделить несколько важных закономерностей, справедливых в случае вписанных углов, которые пригодятся при решении задач по геометрии:

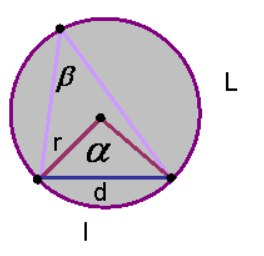
• вписанный угол равен 1/2 центрального угла, который опирается на ту же дугу: \(\beta =\frac{\alpha }{2};\)
• длина хорды составляет: \(l =2r*\sin \frac{\alpha }{2}=2r*\sin \beta;\)
• длина дуги равна: \(l =\alpha *r\), угол \(\alpha\) в радианах;
• длину окружности можно вычислить по формуле: \(L=2\pi *r;\)
• площадь круга определяется, как: \(S=\pi r^{2}.\)

Формулировка теоремы о вписанном угле, ее следствия

Исходя из определения, вписанный угол содержит такое количество угловых радиусов, минут и секунд, сколько включает половина дуги, которая служит его опорой. Для доказательства теоремы необходимо рассмотреть три разных случая расположения вписанного угла.

В первом случае центр окружности O находится на стороне вписанного угла ABС.

Если построить радиус AO, то получится треугольник АBO. В данной геометрической фигуре радиусы в виде отрезков OA и OB будут равны. Таким образом, угол ABO равен углу BAO. Относительно рассматриваемого треугольника, угол AOС является внешним. В связи с этим, данный угол соответствует сумме углов ABO и BAO, а также равен двойному углу ABO. Можно сделать вывод, что угол ABO является половиной центрального угла AOС. С другой стороны, этот угол измеряется дугой AC. Таким образом, вписанный угол ABС равен половине дуги AC.

Во втором случае центр окружности O расположен между сторонами вписанного угла ABС.

С помощью построения диаметра BD угол ABС будет поделен на два угла. Один из рассматриваемых углов, согласно доказательству теоремы в первом случае, равен половине дуги AD. Второй угол соответствует половине дуги СD. Таким образом, угол ABС определен, как (AD+DС) /2, то есть 1/2 AC.

В третьем случае центр окружности O не принадлежит вписанному углу ABС.

Построив диаметр BD, получим, что угол ABС равен равности углов ABD и CBD. Однако, углы ABD и CBD измеряются, согласно доказанной ранее теореме, половинами дуг AD и СD. Исходя из того, что угол ABС соответствует половине разности (AD-СD), он равен половине дуги АС.

Теорема о вписанном в окружность угле обладает несколькими следствиями.

Чему равен вписанный угол в окружности

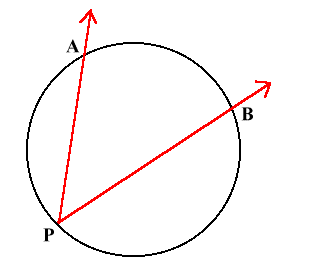
Вписанный в круг угол состоит из двух хорд и вершины, которая расположена на окружности. К примеру, треугольник АВС имеет вписанный угол АРВ, который образован парой лучей и вершиной, принадлежащей окружности:

Величина вписанного угла соответствует ½ его дуги, то есть составляет ½ дуги АВ: APB=84/2 = 42.

В том случае, когда пара углов опирается на одну и ту же дугу, они будут равны друг другу. Например, угол BAC равен углу BDC, исходя из того, что данные углы опираются на одну и ту же дугу:

\(∠ CAB = \frac{1}{2} ∠BOC\)

\(∠ CDB =\frac{1}{2} ∠ BOC\)

При известной длине малой дуги и радиусе, вписанный угол можно вычислить по формуле:

\(X= \frac{90*L\pi }{R}\)

Предположим, что в окружности построили хорду AB. По разные стороны от нее отметили точки C и D, и соединили их с концами хорды. Полученный угол ACB больше, чем угол ADB в два раза. Так как углы ACB и ADB опираются на одну хорду и расположены по разные стороны от нее, то в сумме рассматриваемые углы составляют 180 градусов. Если принять \(\angle ADB\) за x, то \(\angle ACB\) составит 2x, а их сумма равна:

x+2x=180

При решении данного уравнения, x=60. Таким образом:

\(\angle ADB={{60}^{\circ}},\ \text{a}\ \angle ACB={{120}^{\circ}}\)

В результате, \(\angle ADB={{60}^{\circ}}, \ \angle ACB={{120}^{\circ}}\)