Вписанный угол, опирающийся на диаметр
Что такое вписанный угол, опирающийся на диаметр
Вписанный угол — это угол, вершина которого лежит на окружности, а стороны являются хордами.
Хорда — это отрезок, соединяющий две точки на окружности.
Вписанный угол измеряется половиной дуги, на которую опирается. Формула нахождения вписанного угла:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
∠ACB=AB/2
Вписанный угол, который опирается на диаметр, всегда прямой.
Какими свойствами обладает
Свойства вписанных углов:
- Вписанные углы, опирающиеся на одну и ту же дугу равны.
- Вписанные углы равны половине центрального (центральный угол — угол, вершина которого расположена в центре окружности), который опирается на ту же дугу.
- Вписанный угол, опирающийся на полуокружность равен 90º. Это утверждение тождественно утверждению, что впсианный угол, опирающийся на диаметр, всегда прямой.
- На одну и ту же дугу может опираться бесконечное множество вписанных углов.
Теорема Фалеса, доказательство по шагам
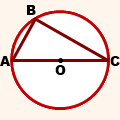
Теорема Фалеса: если в треугольнике угол опирается на диаметр окружности, описанной вокруг него, то угол прямой, то есть треугольник прямоугольный.
Доказательство:
Дано: AC — диаметр, ∠ABC — вписанный
Доказать: ∠ABC=90º
Доказательство:
- Так как AC — диаметр, то ∠AOC=180º.
- ∠AOC — центральный, а ∠ABC — вписанный, опирающийся на ту же дугу.
- Следовательно можно использовать теорему о вписанном угле: вписанные углы равны половине центрального, который опирается на ту же дугу.
\(∠ABC=∠AOC/2=180/2=90º\), что и требовалось доказать.
Задачи для самостоятельного решения
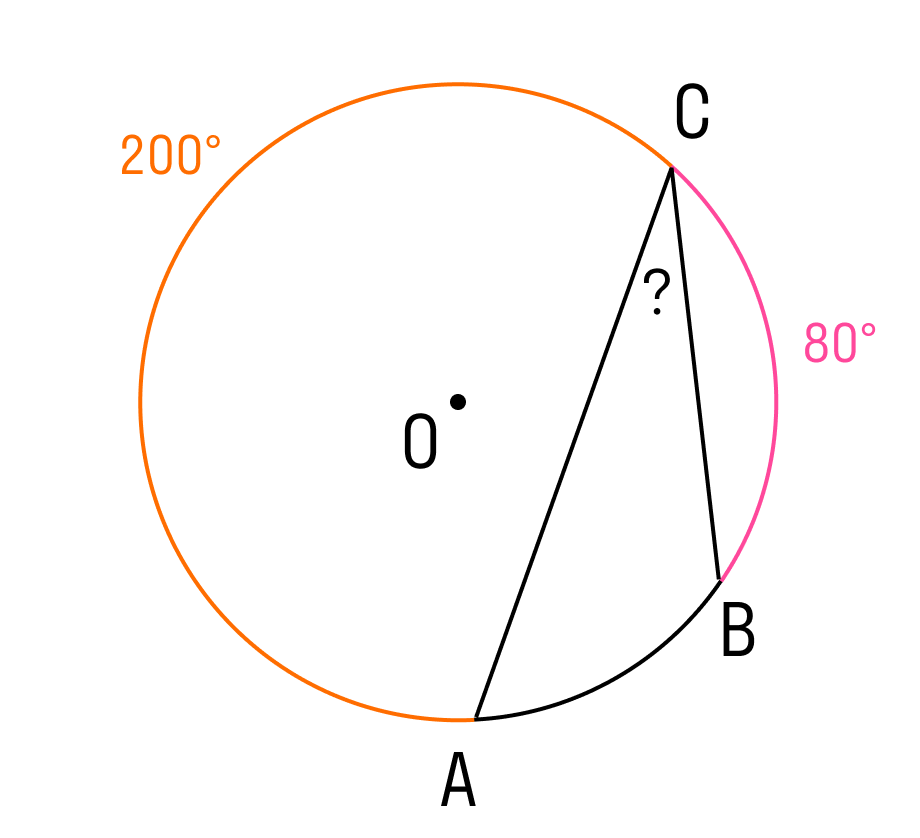
Дана окружность, дуга AC = 200°, дуга BC = 80°. Найдите величину вписанного угла, опирающегося на дугу AB. ㄥACB = ?
Дана окружность, ㄥAOC = 140°, найдите, чему равна величина вписанного угла.
Ответы
Задача 1
Ответ: 40º. Для решения необходимо вычислить значение дуги АВ, а затем воспользоваться правилом: вписанный угол равен половине дуги, на которую он опирается.
Задача 2
Ответ: 70º. ㄥAOC = 140° — центральный, ㄥAВC — вписанный, опирается на ту же дугу, что и центральный. По свойству о том, что вписанный угол равен половине центрального, если они опираются на одну дугу: ㄥAВC=140/2=70.
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так